位图索引
位图法就是Bitmap的缩写。所谓Bitmap,就是用每一位来存放某种状态,适用于大规模数据,但数据状态又不是很多的情况。通常是用来判断某个数据存不存在的。
Bit即比特,是目前计算机系统里边数据的最小单位,8个bit即为一个Byte。一个bit的值,或者是0,或者是1;也就是说一个bit能存储的最多信息是2。Bitmap可以理解为通过一个bit数组来存储特定数据的一种数据结构;由于bit是数据的最小单位,所以这种数据结构往往是非常节省存储空间。
比如一个公司有8个员工,现在需要记录公司的考勤记录,传统的方案是记录下每天正常考勤的员工的ID列表,比如2012-01-01:[1,2,3,4,5,6,7,8]。假如员工ID采用byte数据类型,则保存每天的考勤记录需要N个byte,其中N是当天考勤的总人数。另一种方案则是构造一个8bit(01110011)的数组,将这8个员工跟员工号分别映射到这8个位置,如果当天正常考勤了,则将对应的这个位置置为1,否则置为0;这样可以每天采用恒定的1个byte即可保存当天的考勤记录。
综上所述,Bitmap节省大量的存储空间,因此可以被一次性加载到内存中。再看其结构的另一个更重要的特点,它也显现出巨大威力:就是很方便通过位的运算(AND/OR/XOR/NOT),高效的对多个Bitmap数据进行处理,这点很重要,它直接的支持了多维交叉计算能力。比如上边的考勤的例子里,如果想知道哪个员工最近两天都没来,只要将昨天的Bitmap和今天的Bitmap做一个按位的“OR”计算,然后检查那些位置是0,就可以得到最近两天都没来的员工的数据了,比如:
再比如,我们想知道哪些男员工没来?我们可以在此结果上再“And”上一个Bitmap就能得到结果。
位图索引与B-Tree索引
位图索引由于其结构的特殊性,所以在存储空间和特定列的查询性能上都存在一定优势,但是在传统以处理事务为主的数据库领域,我们使用较多的依然还是B-tree或者B-tree变种类型索引。我们将总结传统位图索引与B-tree索引技术各自的结构特点、优势、局限性以及适用场景。
位图索引:
每列的key对应一个bit序列。
可以利用计算机硬件对位逻辑操作的强力支持,从而使单列内部的操作有效转换为按位逻辑操作。
多列之间的结果聚合也可以有效转化为按位逻辑操作。
更新操作慢,并发性能差。适用于只读、较少更新或者追加的数据集上的查询操作。
B-Tree索引:
逻辑构造为一颗N叉平衡树;每列中的key对应一个Row ID数组。
低基数情况下,索引结构空间冗余。B-Tree上存在大量相邻相同键值的叶子结点,造成严重的空间与I/O扫描浪费。
单一索引路径选择问题。即SQL条件中包含多列时,即使每个列对应一个索引,在执行中也只能沿着一个索引的执行路径,而其他列只能作为一种筛选条件。
树状结构适合频繁的更新操作。适用于事务性数据库
布隆过滤器
是一个很长的二进制向量和一系列随机映射函数。布隆过滤器可以用于检索一个元素是否在一个集合中。它的优点是空间效率和查询时间都远远超过一般的算法,缺点是有一定的误识别率和删除困难。
如果想判断一个元素是不是在一个集合里,一般想到的是将集合中所有元素保存起来,然后通过比较确定。链表、树、散列表等等数据结构都是这种思路。但是随着集合中元素的增加,我们需要的存储空间越来越大。同时检索速度也越来越慢,上述三种结构的检索时间复杂度分别为O(n),O(\log n),O(n/k)。
布隆过滤器的原理是,当一个元素被加入集合时,通过K个散列函数将这个元素映射成一个位数组中的K个点,把它们置为1。检索时,我们只要看看这些点是不是都是1就(大约)知道集合中有没有它了:如果这些点有任何一个0,则被检元素一定不在;如果都是1,则被检元素很可能在。这就是布隆过滤器的基本思想。
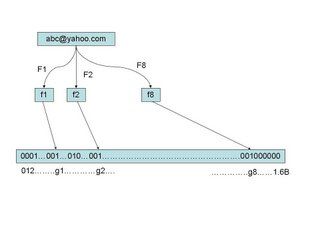
假定我们存储一亿个电子邮件地址,我们先建立一个十六亿二进制(比特),即两亿字节的向量,然后将这十六亿个二进制全部设置为零。对于每一个电子邮件地址 X,我们用八个不同的随机数产生器(F1,F2, ...,F8) 产生八个信息指纹(f1, f2, ..., f8)。再用一个随机数产生器 G 把这八个信息指纹映射到 1 到十六亿中的八个自然数 g1, g2, ...,g8。现在我们把这八个位置的二进制全部设置为一。当我们对这一亿个 email 地址都进行这样的处理后。一个针对这些 email 地址的布隆过滤器就建成了。(见下图)
现在,让我们看看如何用布隆过滤器来检测一个可疑的电子邮件地址 Y 是否在黑名单中。我们用相同的八个随机数产生器(F1, F2, ..., F8)对这个地址产生八个信息指纹 s1,s2,...,s8,然后将这八个指纹对应到布隆过滤器的八个二进制位,分别是 t1,t2,...,t8。如果 Y 在黑名单中,显然,t1,t2,..,t8 对应的八个二进制一定是一。这样在遇到任何在黑名单中的电子邮件地址,我们都能准确地发现。
优点
相比于其它的数据结构,布隆过滤器在空间和时间方面都有巨大的优势。布隆过滤器存储空间和插入/查询时间都是常数(O(k))。另外,散列函数相互之间没有关系,方便由硬件并行实现。布隆过滤器不需要存储元素本身,在某些对保密要求非常严格的场合有优势。
缺点
布隆过滤器的缺点和优点一样明显。误算率是其中之一,随着存入的元素数量增加,误算率随之增加。但是如果元素数量太少,则使用散列表足矣。常见的补救办法是在建立一个小的白名单,存储那些可能别误判的元素。
另外,一般情况下不能从布隆过滤器中删除元素。我们很容易想到把位数组变成整数数组,每插入一个元素相应的计数器加1, 这样删除元素时将计数器减掉就可以了。然而要保证安全地删除元素并非如此简单。
参考
布隆过滤器
数学之美系列二十一 - 布隆过滤器(Bloom Filter)