在密码学中，微型加密算法（Tiny Encryption Algorithm，TEA）是一种易于描述和执行的块密码，通常只需要很少的代码就可实现。其设计者是剑桥大学计算机实验室的大卫·惠勒与罗杰·尼达姆。这项技术最初于1994年提交给鲁汶的快速软件加密的研讨会上，并在该研讨会上演讲中首次发表。
在给出的代码中：加密使用的数据为2个32位无符号整数，密钥为4个32位无符号整数即密钥长度为128位
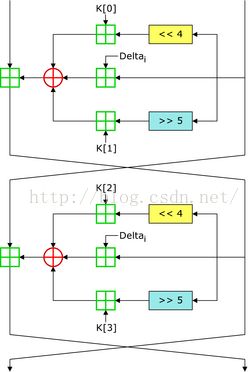
加密过程：
img
算法实现：
示例代码：
C语言代码（需支持C99）
#include
#include
//加密函数
void encrypt (uint32_t* v, uint32_t* k) {
uint32_t v0=v[0], v1=v[1], sum=0, i; /* set up */
uint32_t delta=0x9e3779b9; /* a key schedule constant */
uint32_t k0=k[0], k1=k[1], k2=k[2], k3=k[3]; /* cache key */
for (i=0; i < 32; i++) { /* basic cycle start */
sum += delta;
v0 += ((v1<<4) + k0) ^ (v1 + sum) ^ ((v1>>5) + k1);
v1 += ((v0<<4) + k2) ^ (v0 + sum) ^ ((v0>>5) + k3);
} /* end cycle */
v[0]=v0; v[1]=v1;
}
//解密函数
void decrypt (uint32_t* v, uint32_t* k) {
uint32_t v0=v[0], v1=v[1], sum=0xC6EF3720, i; /* set up */
uint32_t delta=0x9e3779b9; /* a key schedule constant */
uint32_t k0=k[0], k1=k[1], k2=k[2], k3=k[3]; /* cache key */
for (i=0; i<32; i++) { /* basic cycle start */
v1 -= ((v0<<4) + k2) ^ (v0 + sum) ^ ((v0>>5) + k3);
v0 -= ((v1<<4) + k0) ^ (v1 + sum) ^ ((v1>>5) + k1);
sum -= delta;
} /* end cycle */
v[0]=v0; v[1]=v1;
}
int main()
{
uint32_t v[2]={1,2},k[4]={2,2,3,4};
// v为要加密的数据是两个32位无符号整数
// k为加密解密密钥，为4个32位无符号整数，即密钥长度为128位
printf("加密前原始数据：%u %u\n",v[0],v[1]);
encrypt(v, k);
printf("加密后的数据：%u %u\n",v[0],v[1]);
decrypt(v, k);
printf("解密后的数据：%u %u\n",v[0],v[1]);
return 0;
}
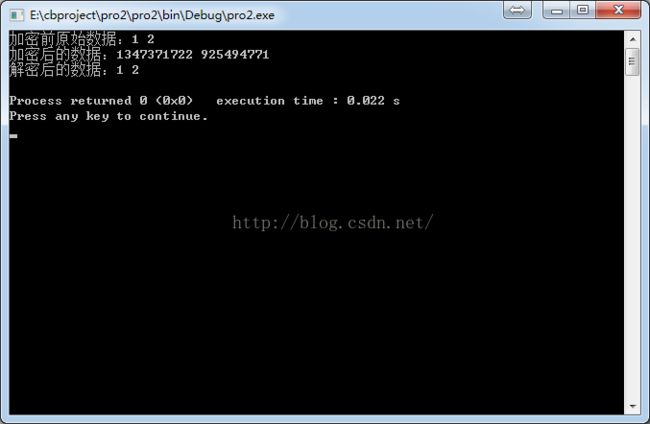
执行结果：
img
加密前原始数据：1 2
加密后的数据：1347371722 925494771
解密后的数据：1 2
Process returned 0 (0x0) execution time : 0.020 s
Press any key to continue.
XTEA是TEA的升级版，增加了更多的密钥表，移位和异或操作等等，设计者是Roger Needham, David Wheeler
加密过程：
img
算法实现：
示例代码：
加密前原始数据：1 2
加密后的数据：1347371722 925494771
解密后的数据：1 2
Process returned 0 (0x0) execution time : 0.020 s
Press any key to continue.
XTEA是TEA的升级版，增加了更多的密钥表，移位和异或操作等等，设计者是Roger Needham, David Wheeler
加密过程：
算法实现：
示例代码：
[cpp] view plain copy
#include
#include
/* take 64 bits of data in v[0] and v[1] and 128 bits of key[0] - key[3] */
void encipher(unsigned int num_rounds, uint32_t v[2], uint32_t const key[4]) {
unsigned int i;
uint32_t v0=v[0], v1=v[1], sum=0, delta=0x9E3779B9;
for (i=0; i < num_rounds; i++) {
v0 += (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + key[sum & 3]);
sum += delta;
v1 += (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + key[(sum>>11) & 3]);
}
v[0]=v0; v[1]=v1;
}
void decipher(unsigned int num_rounds, uint32_t v[2], uint32_t const key[4]) {
unsigned int i;
uint32_t v0=v[0], v1=v[1], delta=0x9E3779B9, sum=delta*num_rounds;
for (i=0; i < num_rounds; i++) {
v1 -= (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + key[(sum>>11) & 3]);
sum -= delta;
v0 -= (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + key[sum & 3]);
}
v[0]=v0; v[1]=v1;
}
int main()
{
uint32_t v[2]={1,2};
uint32_t const k[4]={2,2,3,4};
unsigned int r=32;//num_rounds建议取值为32
// v为要加密的数据是两个32位无符号整数
// k为加密解密密钥，为4个32位无符号整数，即密钥长度为128位
printf("加密前原始数据：%u %u\n",v[0],v[1]);
encipher(r, v, k);
printf("加密后的数据：%u %u\n",v[0],v[1]);
decipher(r, v, k);
printf("解密后的数据：%u %u\n",v[0],v[1]);
return 0;
}
img
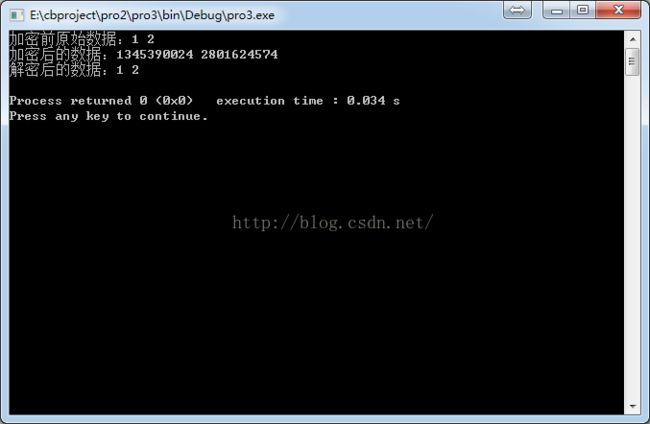
加密前原始数据：1 2
加密后的数据：1345390024 2801624574
解密后的数据：1 2
Process returned 0 (0x0) execution time : 0.034 s
Press any key to continue.
XXTEA，又称Corrected Block TEA，是XTEA的升级版
，设计者是Roger Needham, David Wheeler
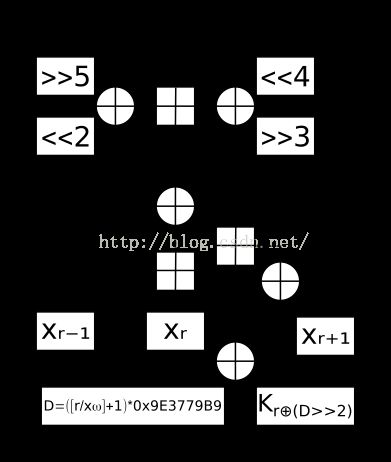
加密过程：
img
算法实现：
示例代码：
#include
#include
#define DELTA 0x9e3779b9
#define MX (((z>>5^y<<2) + (y>>3^z<<4)) ^ ((sum^y) + (key[(p&3)^e] ^ z)))
void btea(uint32_t *v, int n, uint32_t const key[4])
{
uint32_t y, z, sum;
unsigned p, rounds, e;
if (n > 1) /* Coding Part */
{
rounds = 6 + 52/n;
sum = 0;
z = v[n-1];
do
{
sum += DELTA;
e = (sum >> 2) & 3;
for (p=0; p> 2) & 3;
for (p=n-1; p>0; p--)
{
z = v[p-1];
y = v[p] -= MX;
}
z = v[n-1];
y = v[0] -= MX;
sum -= DELTA;
}
while (--rounds);
}
}
int main()
{
uint32_t v[2]= {1,2};
uint32_t const k[4]= {2,2,3,4};
int n= 2; //n的绝对值表示v的长度，取正表示加密，取负表示解密
// v为要加密的数据是两个32位无符号整数
// k为加密解密密钥，为4个32位无符号整数，即密钥长度为128位
printf("加密前原始数据：%u %u\n",v[0],v[1]);
btea(v, n, k);
printf("加密后的数据：%u %u\n",v[0],v[1]);
btea(v, -n, k);
printf("解密后的数据：%u %u\n",v[0],v[1]);
return 0;
}
img
加密前原始数据：1 2
加密后的数据：3238569099 2059193138
解密后的数据：1 2
Process returned 0 (0x0) execution time : 0.369 s
Press any key to continue.
转：http://blog.csdn.net/gsls200808/article/details/48243019