大家好,很高兴可以和大家一起来继续学习机器学习,这几天时间,我着重研究了下主成分分析法,不过因为其数学推理实在有些过于繁琐和复杂,我也没太搞得太清楚,如果在文章当中出现了什么错误,也请各位多多指教.
1:什么是PCA?
主成分分析法是机器学习领域中常用的一种算法,是Pearson在1901年提出的,再后来由hotelling在1933年加以发展提出的一种多变量的统计方法.
主成分分析最主要的用途在于“降维”.通过析取主成分显出的最大的个别差异,也可以用来削减回归分析和聚类分析中变量的数目.
举个例子,你要做一项分析,选中了20个指标,你觉得都很重要,但是20个指标对于你的分析确实太过繁琐,这时候,你就可以采用主成分分析的方法进行降维.
20个指标之间会有这样那样的相互关系,相互之间会有影响,通过主成分分析后,得到4个或者5个主成分指标.此时,这几个主成分指标既涵盖了你20个指标中的绝大部分信息,又让你的分析得到了简化(从20维降到4、5维),简化了分析过程,增加了结果精度.如果在实际情况中,我们如果能用不超过3-5个的成分就可以解释数据变异的80%,这就可以算作为成功.
现在我们用R语言来做一个相关的PCA实例:
首先我们先来介绍下我们下边将要使用的主成分分析的相关函数:
1:princomp函数:
做主成分分析最主要的函数是princomp()函数,使用的格式为:
princomp(formula,data = NULL,subset,na.action,...)
其中formula是没有响应变量的公式,类似于回归分析和方差分析中但是没有响应的变量.data是数据框,类似于回归分析和方差分析.
2:summary函数:
summary函数与在回归分析中的用法相同,其主要的目的就是提取主成分的信息,主要的格式为:
summary(object,loadings = FALSE,cutoff = 0.1,...)
其中object是由princomp()得到的对象,loadings是逻辑变量,当loadings = TRUE时表示显示loading中的内容,当为FALSE时则不显示.
3:loadings函数:
loadings()函数主要显示主成分分析或者因子分析当中的loadings的内容,在主成分分析中,实际上是对主成分对应的各列,即正交矩阵.在因子分析中,其内容就是载荷因子矩阵,loadings()函数的使用格式为:
loadings(x)
其中x是由函数princomp()得到的对象
4:predict函数:
predict()函数是预测主成分的值,使用的格式为:
predict(object,newdata,...)
当object是由princomp()得到的对象,newdata是由预测值构成的数据框,当newdata缺省时,预测已有数据的主成分值
5:screeplot函数
screeplot()函数是画出主成分的碎石图,主要的格式有:
screeplot(x,npcs = min(10,length(x$sdev)),
type = c("barplot","lines"),
main = deparse(substitute(x)),...)
x princomp()npcs type
其中X是由princomp()得到的对象,npcs是画出主成分的个数,type是描述画出的碎石图的的类型,”barplot”是直方图类型,”lines”是直线图类型.
6:biplot函数
biplot()是画出关于主成分的散点图和原坐标在主成分下的方向,其中的格式为:
biplot(x,choices = 1:2,scale = 1,pc.biplot = FALSE,...)
其中X是由princomp()得到的对象,choices是选择的主成分,缺省值是第一个第二个主要成分,pc.biplot是逻辑变量.
现在我们把函数介绍完了,现在我们开始引用实例来去解决PCA问题:
在跳楼机大学中随机抽取某年级30名学生,测量其身高X1,体重X2,胸围X3和坐高X4,其中数据如下图所示,现在对着30名学生的身体的四项指标做主成分分析
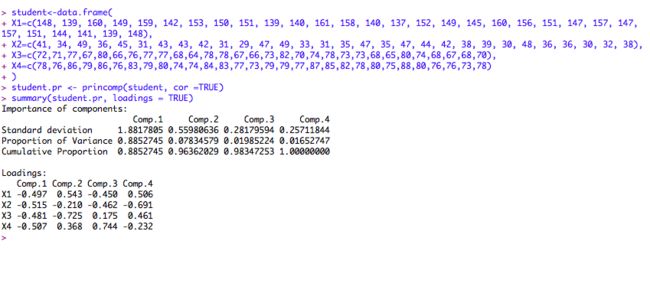
首先,我们先用数据框的形式输入数据,用princomp()作为主成分分析,我在书上看到推荐使用相关的矩阵作为主成分分析更加的合理,因此这里选择的参数是cor=TRUE,最后用summary()列出主成分分析的值,这里选择loadings=TRUE,以下是相应的程序:
在上述程序中,summary函数列出了主成分分析的重要信息,Standard deviation行表示的是主成分的标准差,即主成分的方差的开方,也就是想应的特征值的开方,proporcrion of Variance行表示的是方差的贡献率,Cumulative Proportion行表示的是方差的累计贡献率
由于summary函数中的参数中选取了loadings = true,因此列出的的loading内容实际上就是主成分对应原始变量X1,X2,X3,X4的系数,因此我们可以得到:
因为前面两个的主成分的贡献率可以达到了96%,另外的两个主成分可以舍去,依次来达到降维的目的.
第一主成分对应的系数符号都相似,其中的数值都在0.5左右他反应了跳楼机学生的魁梧程度,身材高大的学生他的对应的其他的部分尺寸也比较大,因此第一主成分的值就比较小,均为负值;而身材矮小的学生,他的其他4部分都比较小.因此第一主成分的绝对值比较大,我们称第一主成分为大小因子,第二成分为高度和宽度的差,第二主成分大的可以表明这个学生比较瘦高,较小的可以看为”矮胖”.因此把第二主成分看为体型因子.
我们看一下各样本主成分的值,这个时候要使用predict()函数:
从第一主成分看,较小的几个值是25号样本,3号样本和5号样本,这说明这结果学生身材魁梧,而11,15,29的值比较大,说明这几个学生身材瘦小.
从第二主成分来看,较大的几个值是23,19,4号样本,说明这几个学生比较瘦比较高,17,8,2号样本这样的就属于矮胖了.
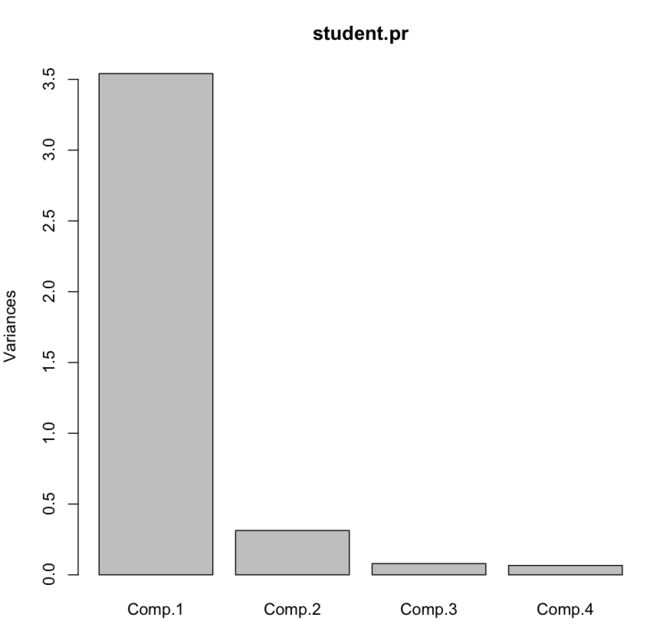
现在画出主成分的碎石图:
screeplot(student.pr,type="lines")
还可以画出第一主成分和第二主成分的样本直方图
好了,这就是这篇文章我想要阐述的一些东西,虽然看起来很简单,但是实际上后边的原理难以搞得一清二楚,接下来一段时间我将要研究主成分分析的一些应用,比如变量分类问题和主成分的回归问题,虽然这是个艰难的过程,但我相信其中的乐趣大于这些困难,加油吧!