在讲 LZW 在 GIF 中的应用前,有必要先简单的过一下 LZW 算法。
LZW算法又叫“串表压缩算法”就是通过建立一个字符串表,用较短的代码来表示较长的字符串来实现压缩。 LZW压缩算法是Unisys的专利,有效期到2003年,所以对它的使用已经没有限制了
在上面的介绍中,关键在于字符串表这一概念,为了简单理解,我举一个例子(此例子并不是完全使用的 LWZ 算法,但思想是一致的)。
假设有以下字符串:AABCCBACBCBAABC
如果这时有以下字符串表:
| 码 | 字符串 |
|---|---|
| 0 | A |
| 1 | B |
| 2 | C |
| 3 | AA |
| 4 | BC |
| 5 | CB |
| 6 | AC |
| 7 | BCB |
| 8 | AAB |
那么以上的字符串就可以用字符串表中的码来表示,其中一种表示方法为:345678。可以看到只用了 6 个字符就表示了长度为 15 的字符串。当然这个只是我为了大家好理解随意些的一个表,真正的 LZW 算法生成表的算法相对比较复杂。到这里你只需要理解字符串表的作用即可,不必纠结表中的内容是如何生成的(其实是我胡乱编的,没有使用 LZW 算法)。
LZW 在 GIF 中的压缩与解压缩过程
LZW 在对文本进行压缩的时候建立的是字符串表,其中每个码对应的是一个字符串。而在 GIF 中并不是字符串表,而是颜色索引表。其中码不变,而字符串则变成了某种颜色在 Global Color Table 或 Local Color Table 中的索引。因为本身使用这两个表也是为了对颜色数据有一个压缩效果。
在上一篇《GIF 字节格式介绍》中 Image Data 一节,讲到 LZW Minimum Code Size 的时候并没有过多介绍,这里我详细解释一下它的意思。
在 LZW 中,在进行压缩之前,其实已经存在了字符串表或颜色索引表的一部分。在文本压缩中(英文压缩,忽略字母大小写以及字母以外的字符),已经存在了一个大小为 26 的,字符串表,其中码的范围为 0 ~ 25,字符串分别为 A~Z。这时候 minimum code 的值为 28(minmum code size为 5) 。那么为什么会跳过中间的 26 和 27 呢?其实紧跟在初始表码后的两个数有它特殊的用处,其分别是 清空码(clear code)和信息终止码(end of information code)。
而对于 GIF 图来说,其颜色支持 2^(2~8) 种,所以其初始化表如下:
| LZW Mini Code Size | 颜色码 | 清空码 | 信息终止码 |
|---|---|---|---|
| 2 | #0 - #3 | #4 | #5 |
| 3 | #0 - #7 | #8 | #9 |
| 4 | #0 - #15 | #16 | #17 |
| 5 | #0 - #31 | #32 | #33 |
| 6 | #0 - #63 | #64 | #65 |
| 7 | #0 - #127 | #128 | #129 |
| 8 | #0 - #255 | #256 | #257 |
而这里的清空码和信息终止码有什么用呢?一般说来,当遇到清空码的时候,我们就要把之前生成的表重置为初始状态。而当遇到信息终止码的时候,则说明压缩或解压缩到此为止。
那这里为什么需要在遇到清空码的时候重置表呢?这其实也是为了压缩效率考虑,是想一下,如果一个文本包含千万个字母,那如果不对表中的码的长度做一个限制,可能会出现一个很大很大的数字。这在 LZW 中是被禁止的。在 LZW 的不同运用场景中,这个码的长度有不同的要求,在 GIF 中码被限制在了 12 位以内。
GIF 的 LZW压缩
首先我们还是使用《GIF 字节格式介绍》中的实例图:
其放大后的效果图如下:
其全局颜色表:
| 索引 | 字节组合 | 颜色 |
|---|---|---|
| 0 | FFFFFF | 白色 |
| 1 | FF0000 | 红色 |
| 2 | 0000FF | 蓝色 |
| 3 | 000000 | 黑色 |
其初始的颜色索引表为:
| 码 | 索引 |
|---|---|
| #0 | 0 |
| #1 | 1 |
| #2 | 2 |
| #3 | 3 |
| #4 | 清空码 |
| #5 | 信息终止码 |
其每个像素的颜色对应的索引如下:
1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 1, 1, 1, 0, 0, 0, 0, 2, 2, 2, 1, 1, 1, 0, 0, 0, 0, 2, 2, 2, ...
在描述压缩过程前,需要先约定几个需要使用的变量:
- 输入流(Index Stream):即上面给出的颜色对应的索引数据流
- 输出流(Code Stream):即压缩后的码流
- 索引缓存(Index Buffer):在压缩过程中用来暂存颜色索引的值(它可以是一个数组)
- K:用来存储缓存后面的那个索引值
一下用 (index ...) 表示索引缓存,[index] 表示 K。
在压缩的初期会有一个初始化的步骤,这一步中我们取输入流中的第一个数据存入索引缓存,K 暂时没有值。然后往输出流里面写一个清空码,这里的话是 #4。
| 步骤 | 动作 | 输入流 | 颜色索引列表新增行 | 输出流 |
|---|---|---|---|---|
| 0 | 初始化 | (1) 1 1 1 1 2 2 2 2 2 1 1 1 1 ... | #4 |
初始化完成后的数据如上,下面进入循环。
先将索引缓存后面的值读入 K,如下:
| 步骤 | 动作 | 输入流 | 颜色索引列表新增行 | 输出流 |
|---|---|---|---|---|
| 0 | 初始化 | (1) 1 1 1 1 2 2 2 2 2 1 1 1 1 ... | #4 | |
| 1 | 读取 | (1) [1] 1 1 1 2 2 2 2 2 1 1 1 1 ... | #4 |
给 K 赋值完成后我们就需要看索引缓存 + K 的集合是否在颜色索引表中存在,这里索引缓存 + K = (1,1),很显然我们的颜色索引表目前还是初始化状态,并没有 (1,1) 这个索引组合。那么就向颜色索引表中添加 #6 - (1,1) 这条数据。此时我们还需要往输出流写一个码,很多人可能会觉的是 #6,但事实上我们要写的是此时索引缓存中值所对应的码,此时的索引缓存是 (1),其对应的码为 #1。接着将索引缓存的值设为 K,并将 K 的值清空(以上为没有找到索引缓存 + K 的操作)。最后数据如下图:
| 步骤 | 动作 | 输入流 | 颜色索引列表新增行 | 输出流 |
|---|---|---|---|---|
| 0 | 初始化 | (1) 1 1 1 1 2 2 2 2 2 1 1 1 1 ... | #4 | |
| 1 | 读取 | (1) [1] 1 1 1 2 2 2 2 2 1 1 1 1 ... | #4 | |
| 2 | 没有找到索引缓存 + K | 1 (1) 1 1 1 2 2 2 2 2 1 1 1 1 ... | #6 - (1,1) | #4 #1 |
在读取 K 的值,读取完数据如下:
| 步骤 | 动作 | 输入流 | 颜色索引列表新增行 | 输出流 |
|---|---|---|---|---|
| 0 | 初始化 | (1) 1 1 1 1 2 2 2 2 2 1 1 1 1 ... | #4 | |
| 1 | 读取 K | (1) [1] 1 1 1 2 2 2 2 2 1 1 1 1 ... | #4 | |
| 2 | 没有找到索引缓存 + K | 1 (1) 1 1 1 2 2 2 2 2 1 1 1 1 ... | #6 - (1,1) | #4 #1 |
| 3 | 读取 K | 1 (1) [1] 1 1 2 2 2 2 2 1 1 1 1 ... | #4 #1 |
给 K 赋值以后我们继续看索引缓存 + K 的集合是否存在在颜色索引表,此时索引缓存 + K = (1,1),很熟悉嘛,这不就是刚刚往颜色索引表添加的 #6 吗?此时我们不需要也没有新的组合可以往颜色索引表添加,也不需要往输出流写码。我们需要做的就是索引缓存 + K 的值赋给索引缓存,并将 K 的值清空(以上为找到索引缓存 + K 的操作)。最后的数据如下:
| 步骤 | 动作 | 输入流 | 颜色索引列表新增行 | 输出流 |
|---|---|---|---|---|
| 0 | 初始化 | (1) 1 1 1 1 2 2 2 2 2 1 1 1 1 ... | #4 | |
| 1 | 读取 K | (1) [1] 1 1 1 2 2 2 2 2 1 1 1 1 ... | #4 | |
| 2 | 没有找到索引缓存 + K | 1 (1) 1 1 1 2 2 2 2 2 1 1 1 1 ... | #6 - (1,1) | #4 #1 |
| 3 | 读取 K | 1 (1) [1] 1 1 2 2 2 2 2 1 1 1 1 ... | #4 #1 | |
| 4 | 找到索引缓存 + K | 1 (1 1) 1 1 2 2 2 2 2 1 1 1 1 ... | #4 #1 |
接着再读取 K 的值,读取后数据如下:
| 步骤 | 动作 | 输入流 | 颜色索引列表新增行 | 输出流 |
|---|---|---|---|---|
| 0 | 初始化 | (1) 1 1 1 1 2 2 2 2 2 1 1 1 1 ... | #4 | |
| 1 | 读取 K | (1) [1] 1 1 1 2 2 2 2 2 1 1 1 1 ... | #4 | |
| 2 | 没有找到索引缓存 + K | 1 (1) 1 1 1 2 2 2 2 2 1 1 1 1 ... | #6 - (1,1) | #4 #1 |
| 3 | 读取 K | 1 (1) [1] 1 1 2 2 2 2 2 1 1 1 1 ... | #4 #1 | |
| 4 | 找到索引缓存 + K | 1 (1 1) 1 1 2 2 2 2 2 1 1 1 1 ... | #4 #1 | |
| 5 | 读取 K | 1 (1 1) [1] 1 2 2 2 2 2 1 1 1 1 ... | #4 #1 |
这时候应该知道要干嘛了吧,索引缓存 + K 的值为 (1,1,1),在我们的颜色索引表中并有这个值,这时候我们重复上面没有找到索引缓存 + K的操作即可,最后的数据如下:
| 步骤 | 动作 | 输入流 | 颜色索引列表新增行 | 输出流 |
|---|---|---|---|---|
| 0 | 初始化 | (1) 1 1 1 1 2 2 2 2 2 1 1 1 1 ... | #4 | |
| 1 | 读取 K | (1) [1] 1 1 1 2 2 2 2 2 1 1 1 1 ... | #4 | |
| 2 | 没有找到索引缓存 + K | 1 (1) 1 1 1 2 2 2 2 2 1 1 1 1 ... | #6 - (1,1) | #4 #1 |
| 3 | 读取 K | 1 (1) [1] 1 1 2 2 2 2 2 1 1 1 1 ... | #4 #1 | |
| 4 | 找到索引缓存 + K | 1 (1 1) 1 1 2 2 2 2 2 1 1 1 1 ... | #4 #1 | |
| 5 | 读取 K | 1 (1 1) [1] 1 2 2 2 2 2 1 1 1 1 ... | #4 #1 | |
| 6 | 没有找到 | 1 1 1 (1) 1 2 2 2 2 2 1 1 1 1 ... | #7 - (1,1,1) | #4 #1 #6 |
整个压缩差不多就是这样一个循环找索引缓存 + K 的步骤,下图是执行到26步后的数据,你可以参考看看自己是否掌握了 LZW 的压缩算法。
| 步骤 | 动作 | 输入流 | 颜色索引列表新增行 | 输出流 |
|---|---|---|---|---|
| 0 | 初始化 | (1) 1 1 1 1 2 2 2 2 2 1 1 1 1 ... | #4 | |
| 1 | 读取 K | (1) [1] 1 1 1 2 2 2 2 2 1 1 1 1 ... | #4 | |
| 2 | 没有找到索引缓存 + K | 1 (1) 1 1 1 2 2 2 2 2 1 1 1 1 ... | #6 - (1,1) | #4 #1 |
| 3 | 读取 K | 1 (1) [1] 1 1 2 2 2 2 2 1 1 1 1 ... | #4 #1 | |
| 4 | 找到索引缓存 + K | 1 (1 1) 1 1 2 2 2 2 2 1 1 1 1 ... | #4 #1 | |
| 5 | 读取 K | 1 (1 1) [1] 1 2 2 2 2 2 1 1 1 1 ... | #4 #1 | |
| 6 | 没有找到 | 1 1 1 (1) 1 2 2 2 2 2 1 1 1 1 ... | #7 - (1,1,1) | #4 #1 #6 |
| 7 | 读取 K | 1 1 1 (1) [1] 2 2 2 2 2 1 1 1 1 ... | #4 #1 #6 | |
| 8 | 找到索引缓存 + K | 1 1 1 (1 1) 2 2 2 2 2 1 1 1 1 ... | #4 #1 #6 | |
| 9 | 读取 K | 1 1 1 (1 1) [2] 2 2 2 2 1 1 1 1 ... | #4 #1 #6 | |
| 10 | 没有找到索引缓存 + K | 1 1 1 1 1 (2) 2 2 2 2 1 1 1 1 ... | #8 - (1,1,2) | #4 #1 #6 #6 |
| 11 | 读取 K | 1 1 1 1 1 (2) [2] 2 2 2 1 1 1 1 ... | #4 #1 #6 #6 | |
| 12 | 没有找到索引缓存 + K | 1 1 1 1 1 2 (2) 2 2 2 1 1 1 1 ... | #9 - (2,2) | #4 #1 #6 #6 #2 |
| 13 | 读取 K | 1 1 1 1 1 2 (2) [2] 2 2 1 1 1 1 ... | #4 #1 #6 #6 #2 | |
| 14 | 找到索引缓存 + K | 1 1 1 1 1 2 (2 2) 2 2 1 1 1 1 ... | #4 #1 #6 #6 #2 | |
| 15 | 读取 K | 1 1 1 1 1 2 (2 2) [2] 2 1 1 1 1 ... | #4 #1 #6 #6 #2 | |
| 16 | 没有找到索引缓存 + K | 1 1 1 1 1 2 2 2 (2) 2 1 1 1 1 ... | #10 - (2,2,2) | #4 #1 #6 #6 #2 #9 |
| 17 | 读取 K | 1 1 1 1 1 2 2 2 (2) [2] 1 1 1 1 ... | #4 #1 #6 #6 #2 #9 | |
| 18 | 找到索引缓存 + K | 1 1 1 1 1 2 2 2 (2 2) 1 1 1 1 ... | #4 #1 #6 #6 #2 #9 | |
| 19 | 读取 K | 1 1 1 1 1 2 2 2 (2 2) [1] 1 1 1 ... | #4 #1 #6 #6 #2 #9 | |
| 20 | 没有找到索引缓存 + K | 1 1 1 1 1 2 2 2 2 2 (1) 1 1 1 ... | #11 - (2,2,1) | #4 #1 #6 #6 #2 #9 #9 |
| 21 | 读取 K | 1 1 1 1 1 2 2 2 2 2 (1) [1] 1 1 ... | #4 #1 #6 #6 #2 #9 #9 | |
| 22 | 找到索引缓存 + K | 1 1 1 1 1 2 2 2 2 2 (1 1) 1 1 ... | #4 #1 #6 #6 #2 #9 #9 | |
| 23 | 读取 K | 1 1 1 1 1 2 2 2 2 2 (1 1) [1] 1 ... | #4 #1 #6 #6 #2 #9 #9 | |
| 24 | 找到索引缓存 + K | 1 1 1 1 1 2 2 2 2 2 (1 1 1) 1 ... | #4 #1 #6 #6 #2 #9 #9 | |
| 25 | 读取 K | 1 1 1 1 1 2 2 2 2 2 (1 1 1) [1] ... | #4 #1 #6 #6 #2 #9 #9 | |
| 26 | 没有找到索引缓存 + K | 1 1 1 1 1 2 2 2 2 2 1 1 1 (1) ... | #12 - (1,1,1,1) | #4 #1 #6 #6 #2 #9 #9 #7 |
当处理完所有的数据后不要忘记在最后加上一个信息终止码,在这里的 #5。
最终的输出流如下:
#4 #1 #6 #6 #2 #9 #9 #7 #8 #10 #2 #12 #1 #14 #15 #6 #0 #21 #0 #10 #7 #22 #23 #18 #26 #7 #10 #29 #13 #24 #12 #18 #16 #36 #12 #5
可以看到通过 LZW 的压缩,把原本 10*10 = 100 个数据压缩到了36个码。
GIF 的 LZW 解压缩
在上面一节讲了 LZW 在 GIF 中对每一帧图像数据的压缩过程,最终得到的数据如下:
#4 #1 #6 #6 #2 #9 #9 #7 #8 #10 #2 #12 #1 #14 #15 #6 #0 #21 #0 #10 #7 #22 #23 #18 #26 #7 #10 #29 #13 #24 #12 #18 #16 #36 #12 #5
这一节我们要讲解如何根据根据上面的这串压缩的数据获得原始数据,这里需要注意的是在 LZW 的压缩过程中生成的颜色索引表在最后会被清除,所以在解压缩的时候并不是简单的从颜色索引表去取对应的数据,而是需要我们重新再构建新的颜色索引表。
在描述解压缩过程前,还是需要先约定一个变量:
- 输入流(Code Stream):这里的输入流变成了压缩过程中生成的码流。
- 输出流(Index Stream):输出流为图像上颜色对应索引的数据流。
- CODE : 解压过程中读取的码,如 #6。
- CODE - 1 : CODE 前一个码。
- {CODE}:表示 CODE 所表示码的索引,如 #6 - 1,1 那么这时的 {CODE} = {1,1}
- K :解压过程的一个变量。
在进行解压的循环之前,会有一步初始化操作。这一步首先读取码流的第一个元素,通常都是清空码,这里是 #4,它表示接下来我们要建立一个新的颜色索引表。然后读取下一个元素作为 CODE 的值,这里应该是 CODE = #1 。然后在输出流输出 CODE 对应的索引,即 1 。数据见下表:
| 步骤 | 动作 | 输入流 | 颜色索引列表新增行 | 输出流 |
|---|---|---|---|---|
| 0 | 初始化 | #4 (#1) #6 #6 #2 #9 #9 #7 ... | 1 |
类似的,我们用 () 表示 CODE,用 [] 表示 CODE - 1,接着进入循环。CODE 读取下一个元素为 #6,此时 CODE - 1 为 #1。然后我们看 CODE 所对应的码 #6 是否存在在我们的颜色索引表中。这是的索引表应该是初始状态,只有原始的四个码和清空码以及信息终止码。由于 #6 不在表中,我们令 K = {CODE - 1} 的第一个元素,在此时 CODE - 1 = {1},所以 K = 1,然后往颜色索引表添加新的一行数据 {CODE - 1} + K。因为此时的信息终止码为#5,所以接下就应该是 # 6 。此时数据如下:
| 步骤 | 动作 | 输入流 | 颜色索引列表新增行 | 输出流 |
|---|---|---|---|---|
| 0 | 初始化 | #4 (#1) #6 #6 #2 #9 #9 #7 ... | 1 | |
| 1 | 没有找的 CODE | #4 [#1] (#6) #6 #2 #9 #9 #7 ... | #6 - 1,1 | 1,1,1 |
接着再往下,CODE 取值 #6,CODE - 1也为 #6,此时我们发现 CODE 对应的 #6 已经存在于颜色索引表中,这时候将 {CODE} 的第一元素赋值给 K 即 K = 1,然后将 {CODE} 添加到输出流,并且往颜色索引表添加一条新数据 {CODE - 1} + K,此时的 {CODE - 1}为{1,1},所以新数据是{1,1,1}。这一步的数据如下:
| 步骤 | 动作 | 输入流 | 颜色索引列表新增行 | 输出流 |
|---|---|---|---|---|
| 0 | 初始化 | #4 (#1) #6 #6 #2 #9 #9 #7 ... | 1 | |
| 1 | 没有找的 CODE | #4 [#1] (#6) #6 #2 #9 #9 #7 ... | #6 - 1,1 | 1,1,1 |
| 2 | 找到 CODE | #4 #1 [#6] (#6) #2 #9 #9 #7 ... | #7 - 1,1,1 | 1,1,1,1,1 |
下一步,接着来。CODE 为 #2,CODE - 1 为 #6,此时的 CODE 也就是 #2 存在于颜色索引表,所以将 {CODE} 输出到输出流。接着还是把 {CODE} 的第一个值赋值给 K ,即 K = 2,并将 {CODE - 1} + K 添加进颜色索引表,即{1,1,2}。此时数据如下:
| 步骤 | 动作 | 输入流 | 颜色索引列表新增行 | 输出流 |
|---|---|---|---|---|
| 0 | 初始化 | #4 (#1) #6 #6 #2 #9 #9 #7 ... | 1 | |
| 1 | 没有找的 CODE | #4 [#1] (#6) #6 #2 #9 #9 #7 ... | #6 - 1,1 | 1,1,1 |
| 2 | 找到 CODE | #4 #1 [#6] (#6) #2 #9 #9 #7 ... | #7 - 1,1,1 | 1,1,1,1,1 |
| 3 | 找到 CODE | #4 #1 #6 [#6] (#2) #9 #9 #7 ... | #8 - 1,1,2 | 1,1,1,1,1,2 |
到这里差不到知道接下来该如何了。对于找到 CODE 的情况,K 取 {CODE} 的第一个值,找不到的话 K 取 {CODE - 1} 的第一个值。接着讲 {CODE - 1}+K添加进颜色索引表(循环的每一步都要添加)。对于输出的话,如果找到了 CODE,就直接输出 {CODE},若没有找到,则输出 {CODE - 1} + K。下面是执行了 6 步以后的数据,读者可以看一下是否和自己想的一致:
| 步骤 | 动作 | 输入流 | 颜色索引列表新增行 | 输出流 |
|---|---|---|---|---|
| 0 | 初始化 | #4 (#1) #6 #6 #2 #9 #9 #7 ... | 1 | |
| 1 | 没有找的 CODE | #4 [#1] (#6) #6 #2 #9 #9 #7 ... | #6 - 1,1 | 1,1,1 |
| 2 | 找到 CODE | #4 #1 [#6] (#6) #2 #9 #9 #7 ... | #7 - 1,1,1 | 1,1,1,1,1 |
| 3 | 找到 CODE | #4 #1 #6 [#6] (#2) #9 #9 #7 ... | #8 - 1,1,2 | 1,1,1,1,1,2 |
| 4 | 没有找到 CODE | #4 #1 #6 #6 [#2] (#9) #9 #7 ... | #9 - 2,2 | 1,1,1,1,1,2,2,2 |
| 5 | 找到 CODE | #4 #1 #6 #6 #2 [#9] (#9) #7 ... | #10 - 2,2,2 | 1,1,1,1,1,2,2,2,2,2 |
| 6 | 找到 CODE | #4 #1 #6 #6 #2 #9 [#9] (#7) ... | #11 - 2,2,1 | 1,1,1,1,1,2,2,2,2,2,1,1,1 |
最终得到的输出流为:
1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 1, 1, 1, 0, 0, 0, 0, 2, 2, 2, 1, 1, 1, 0, 0, 0, 0, 2, 2, 2, ...
应该与压缩前数据一致。
注意:在解压缩的过程中,如果数据量大,很有可能会读到清空码,如 #4,此时就必须将之前生成的颜色索引表清除,重置为一开始的状态,然后再处理。
码流的处理
码流转字节流
在 GIF 的 LZW 压缩后,我们得到了如下码流:
#4 #1 #6 #6 #2 #9 #9 #7 #8 #10 #2 #12 #1 #14 #15 #6 #0 #21 #0 #10 #7 #22 #23 #18 #26 #7 #10 #29 #13 #24 #12 #18 #16 #36 #12 #5
那么你觉得这段码流会如何转为字节数组呢?你可能会觉得这还不简单,一个码对应一个字节呗。如果你这样想就大错特错了。之前说过 GIF 的码最大支持 12 位,一个字段不够啊。所以在存储码流的时候也是经过处理的。在刚开始的时候每个码只会用(mini code size) + 1 个位表示,本示例中的 mini code size 为 2,所以刚开始只会用三位来表示一个码,由于一个字节有八位,所以最开始的一个字节的组成如下:#4对应的三位 + #1 对应的三位 + #6对应三位中的两位。然后 #6 中剩下的一位放到下一个字节。如果对此难以理解可以看下图:
在以上字节的拼接过程中我们假设当前的 code size 为 SIZE,SIZE 最初的值为 mini code size + 1。而这个值在何时增加其实还要跟 GIF 压缩过程结合在一起。在压缩过程中当我们往颜色索引表添加的码 = 2^SIZE - 1 的时候,就是增加 SIZE 的时候。如刚开始 SIZE 的值是3,所以当我们添加码 #7 的时候,就应该增加 SIZE 的值,为 4 。结合压缩过程的表来看,在进行到第 6 步的时候,我们往颜色索引表添加了 #7,而此时输出的码为 #6,所以当往输出流写下一个不为 #6 的码是,其值就应该用 4 位来表示。而根据表中的第 12 步,下一个非 #6 的码是 #2 。从上图中也能看出来在 2D 这个字节中,最左边的四位表示的码为 #2。
那么为什么 SIZE 要这么做呢?当我们往颜色索引表添加 #7 的时候,下一个产生的码就是 #8 了,而且如果输出 #8 的话必定是需要四位(1000)来表示的。由于一开始我们用三位来表示 #6,所以如果再遇到 #6,我们知道三位来表示他已经足够了。但对于下一个非 #6 的码,编码器不能确定其是否大于3位,所以就统一用四位来表示。
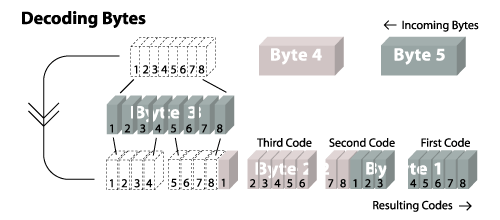
字节流转码流
上面讲的是如何将码流转换为字节流,接着讲如何将字节流转换成码流。道理都一样,刚开始读取的 SIZE 大小为 3。我们看上图的 8C 这个字节,最开始读最右边 3 位,‘100’ = #4,清空码没啥问题。接着是#1,#6,#6。读这三个码的时候用的还是三位,在看下一个码 #2,这时用了四位。我们还是结合解码的图表看,当处理完第二个 #6 后(第 2 步)我们往颜色索引表添加了 #7 - 1,1,1。这里的 7 正好等于 2^3 - 1。也就是说当往颜色索引表添加的码 = 2^SIZE - 1 的时候,SIZE 就需要做加 1 的处理了。
下图是当 SIZE = 5的时候,字节的处理示意图:
字节流转码流实战
在《GIF 字节格式介绍》中的 Image Data 小节,我们的得到了 Image Data 的字节数组如下:
02 16 8C 2D 99 87 2A 1C DC 33 A0 02 75 EC 95 FA A8 DE 60 8C 04 91 4C 01 00
其中 02 用于表示 mini code size = 2,那么此时的 SIZE = 3 。下一个字节 16 表示为十六进制,表示在它之后有 22 个字节是用码流转换而来的。
第一个字节为 8C = 1 0 - 0 0 1 - 1 0 0,首先取右边三位 1 0 0,为 #4,再取中间三位 0 0 1 为 #1,在进行取码的操作同时需要进行解码操作,解码操作可对照GIF 的 LZW 解压缩这一节的图表。
第二个字节为 2D = 0 0 1 0 - 1 1 0 - 1,首先去最右边第一位 1 和第一个字节剩下的 1 0 组合成 1 1 0 为 # 6,接着是中间的 1 1 0 为 #6 。根据GIF 的 LZW 解压缩这一节的图表,当得到这个 #6 的时候,SIZE 需要做 + 1 处理,为 4。所以接下来的 0 0 1 0 为 #2 为下一个码。
第三个字节 99 = 1 0 0 1 - 1 0 0 1 ,取右边四位 1 0 0 1,为 #9,左边四位 1 0 0 1 为 #9 。
到此位置我们得到的码流为 #4 #1 #6 #6 #2 #9 #9,与GIF 的 LZW压缩中产生的码流对比是正确没有差别的。
注意:虽然在本文中
GIF 的 LZW 解压缩和字节流转码流是分开将的,但在实际程序中,这两部分是同时进行的,由后者产生码流的同时,由前者根据码流来解压缩。
总结
到此为止,GIF 与 LZW 的相关内容就讲完了,讲得比较粗略。有些细节可能只有在实际编码中才会遇到我没有细讲。如果有问题可以留言,大家一起讨论。