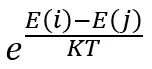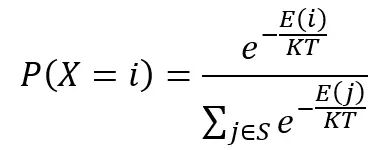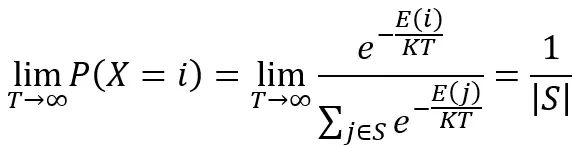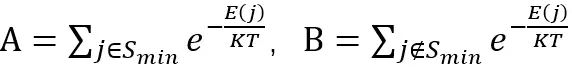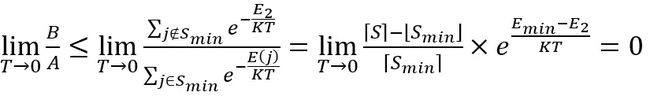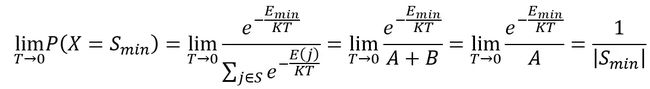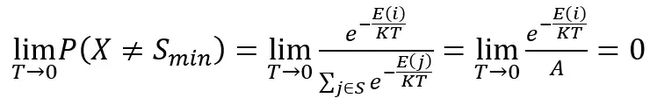姓名：米芃
学号：16040520018
［嵌牛导读］Job-shop问题全称车间作业调度问题（Job-shop scheduling problem），是生产运营管理领域研究的重要课题。进行作业调度问题的研究对于有效缩短产品加工时间，降低产品生产成本，提高企业生产效率等方面有重要的实际应用价值。
［嵌牛鼻子］高效生产 退火算法
［嵌牛提问］如何利用数学进行高效生产？
［嵌牛正文］
因此在该问题研究过程中，逐渐形成一些基准问题，即Job-shop benchmark问题，目前许多学术论文都以这些基准问题作为对比，检验自己的算法是否能够达到最优解，或者是击中最优解的效率是怎么样。
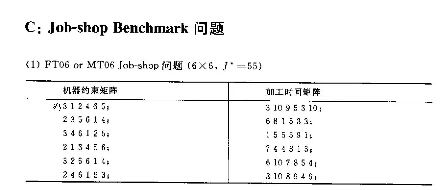
上文截图中的问题是FT06问题，这个问题的最优解即总加工时间为55。因此，如果要解FT06问题，只需确定总加工时间为55，甚至小于55的作业排序方案。
通俗来说，也就是通过建模调度优化工作流程，有效减少工作时间。
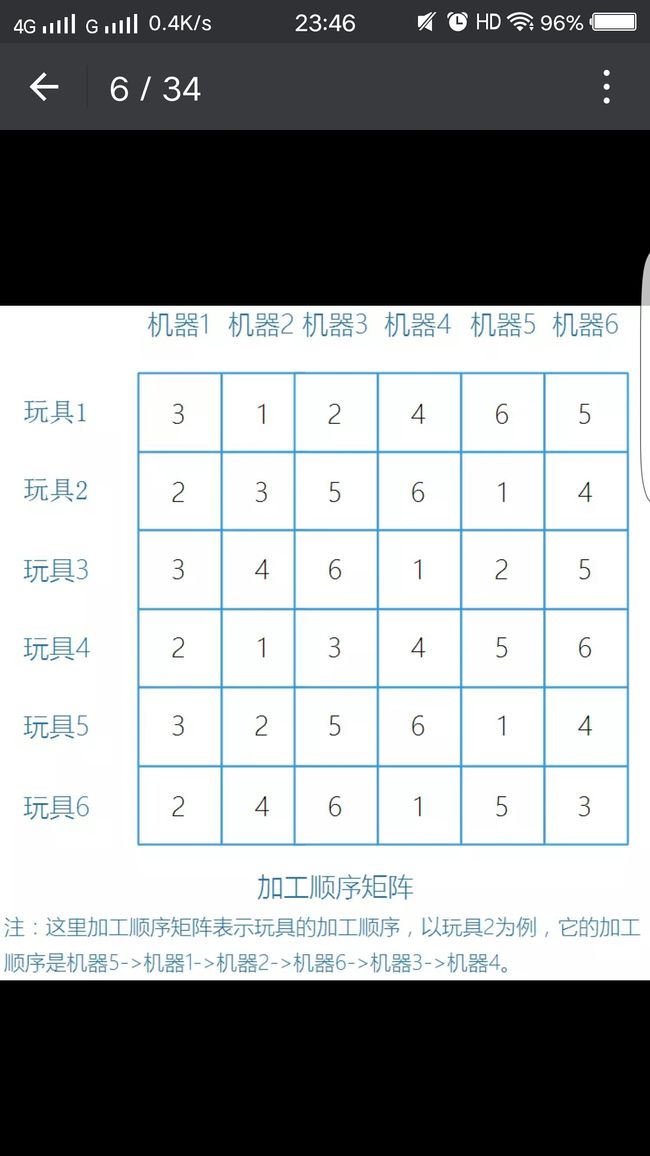
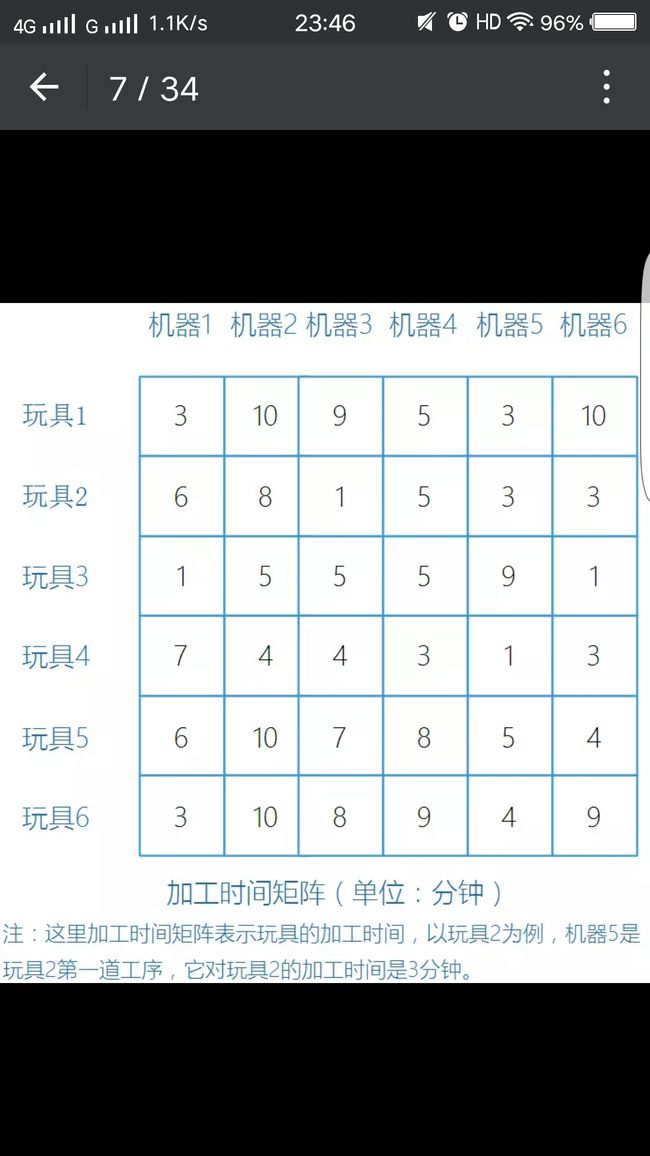
以FT06问题为例，FT06问题实际上可以看作是有6个玩具需要在6台机器上加工，求解最优解。而把FT06问题中的数字翻译一下，则变成下面两个矩阵：加工顺序矩阵和加工时间矩阵。
除此之外，工厂对玩具的加工还有特殊的流程控制：
1、一台机器在同一时刻只能加工一个玩具；
2、一个玩具在同一时刻只能在一台机器上加工。
好了，相信大家对问题已经有所了解，接下来我打算用模拟退火的方式来解答求解。
模拟退火算法：
1983 年，S. Kirkpatrick 等人尝试将退火思想引入到组合优化领域，没想到产生奇效，进而创造出模拟退火算法。事实上，模拟退火算法是基于蒙特卡罗思想的随机寻优算法，其出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。
通俗点来说，就是材料中粒子的不同结构对应于粒子的不同能量水平，在高温条件下，粒子的能量较高，可以自由运动和重新排列。
如果从高温开始非常缓慢地降温，粒子在每个温度下会达到热平衡。当系统完全被冷却时，最终将形成处于低能状态的晶体。
退火过程即固体物质的降温过程中，固体物质内部不断进行重新排列，并逐渐排列成最低能量状态的结构。
算法上的优化过程则是当前解内部不断进行重新排列，并逐渐排列成实现目标函数最小值的解（求目标函数最大值的问题可以转变为求最小值的问题）。
所以会发现，退火过程和优化过程存在明显的相似性。假设材料在状态之下的能量为E(i)，那么材料在温度 T 时从状态 i 进入状态 j 遵循如下规律：
如果 E(i) ≤ E(j)，则接受该状态被转换。
如果 E(i) > E(j)，则状态转换以如下概率被接受：
其中， K 是玻尔兹曼常数， T 是材料温度。
在特定温度下，经过充分的转换以后，材料达到热平衡。这个时候材料处于状态i的概率满足玻尔兹曼分布：
其中， X 表示材料当前状态的随机变量， S 表示状态空间集合。
那么，当温度非常高时，
而当温度下降到很低时，设：
其中：
E2 为仅次于 Emin 的最低能量状态，所以：
也就是说：
当温度降到极低时，材料进入最小能量状态的概率为1！
因此，如果我们运用退火思想放在优化问题上，在降温过程中问题的解进行充分地“热交换”，即进行充分地重新排列，同样可以帮助我们寻找最优解，理论上也会具有达到全局最优解的性能！
这个算法也就是我们常说的“模拟退火算法”。这个时候又遇到了一个问题：怎么构造工厂作业排序优化问题的解？
尝试先构造一个可行解，序列从左到右，可以翻译为，先加工玩具1的工序1，再到加工玩具2的工序1，……，再到加工玩具6的工序1，再到加工玩具1的工序2，再到加工玩具2的工序2……如此类推。
理论上说，假如没有机器的限制，玩具1完成加工工序1的那一刻，可以开始加工玩具2。
但是，因为有机器的限制，如果玩具1的某个步骤要在机器1上加工，假设此时机器1正在加工别的玩具，那么只有等到机器1完成加工的那一刻，才可以开始加工玩具1的下一步骤。
所以，玩具 i 的第 k 个工序在机器 m 上进行加工，其开始时间为：
我们运用这个原则，以自然循环数列为例，按照文章最开头的机器约束矩阵和加工时间矩阵，作一个甘特图，说明这个数列实际上可以表示工厂作业排序优化问题的解。按照这个顺序来执行加工任务，以甘特图来印证：
Step1：执行玩具1的工序1，由机器2来执行，时间为10分钟，对应甘特图机器坐标为M2，时间坐标为0-10。
Step2：执行玩具2的工序1，由机器5来执行，时间为3分钟，对应甘特图机器坐标为M5，时间坐标为0-3。
第3-6步基本类似。我们再聚焦自然循环列第7-10位：1234。按照这个顺序继续执行加工任务, 以甘特图来印证：
Step7：执行玩具1的工序2，由机器3来执行，时间为9分钟。玩具1工序1的结束时间为10，而且机器3先前没有其他任务安排，所以玩具1工序2任务的甘特图机器坐标为M3，时间坐标为10-19。
Step8：执行玩具2的工序2，由机器1来执行，时间为6分钟。玩具2工序1的结束时间为3，而且机器1先前没有其他任务安排，所以玩具2工序2任务的甘特图机器坐标为M1，时间坐标为3-9。
Step 9：执行玩具3的工序2，由机器5来执行，时间为9分钟。玩具3工序1的结束时间为5，机器5先前有任务安排，加工的最后时间为8，所以玩具3工序2的开始时间为 max(5, 8) = 8，甘特图机器坐标为M5，时间坐标为8-17。
Step10：执行玩具4的工序2，由机器1来执行，时间为7分钟。玩具3工序1的结束时间为14，机器1先前有任务安排，加工的最后时间为9，所以玩具4工序2的开始时间为 max(14, 9) = 14，甘特图机器坐标为M1，时间坐标为14-21。
……
流程走到这里，相信大家对整个过程比较明朗了。
按照这个过程，自然循环序列就转变为一张甘特图，进而可以计算出整体的完成时间。
进一步地而言，任何自然循环序列打乱以后的序列，都可以表示这个工厂作业生产优化问题的解。
此时，我们就应该明白解的构造方式了。那接下来这道问题中另一关键点，那就是老解如何变换才能产生新解。
由于目前解的构造方式是一组编码，因此可以对这组编码进行重排，即可产生新解，但也需要考虑到保留当前解的有效成分。
考虑以最简单的方式来产生新解，随机调换：在当前解中随机选择两个位置，并对调它们的数值。算法思想、解的构造、解的产生，这三大问题终于解决了，我们开始设计模拟退火的实现过程了：
第1步，初始化，取一个足够大的初始温度 T0，令当前温度 T = T0，给定一个初始解S1。
第2步，随机调换当前解 S1 的两个位置的数值，产生一个新解 S2 。
第3步，计算增量，Δ = f(S2)– f(S1)，其中f为计算解的总生产时间的函数。
第4步，如果 Δ < 0 则接受 S2 作为新的当前解，S2 = S1 。否则，计算 S2 的接受概率，即在 [0,1] 这个区间上面产生一个均匀分布的随机数rand，如果>rand，则接受 S2 作为新的当前解，否则保留当前解 S1 。
第5步，进行温度衰减，这里采取 T = α × T。
第6步，如果温度没有衰减到设定值 Tend 以下，继续执行第2~5步。
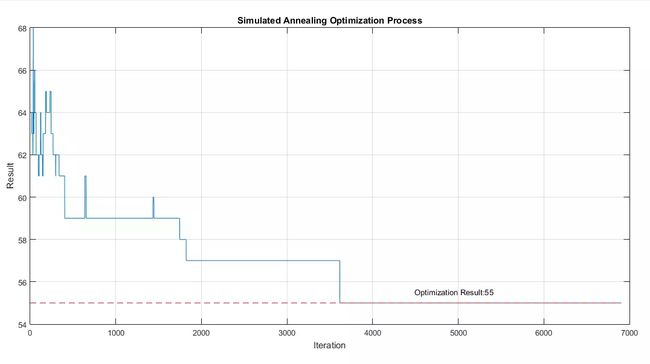
最后，设定模拟退火算法的参数 T0 = 1，α = 0.999，Tend = 10-3，执行模拟退火算法。
而这也正是模拟退火算法的应用所在，通过不断的内部调整，使得结果不断优化，最后达到较佳的状态。