problem sets: binary search; divide and conquer;
lintcode 97. Maximum Depth of Binary Tree, easy
lintcode 480.Binary Tree Paths, easy
lintcode 376.Binary Tree Path Sum, leetcode 112.
lintcode 596 Minimum Subtree
lintcode 595.Binary Tree Longest Consecutive Sequence, leetcode 298
leetcode 114 Flatten Binary Tree to Linked List, lintcode 453
leetcode 235. Lowest Common Ancestor of a Binary Search Tree
lintcode 578.Lowest Common Ancestor III
- leetcode 654. Maximum Binary Tree
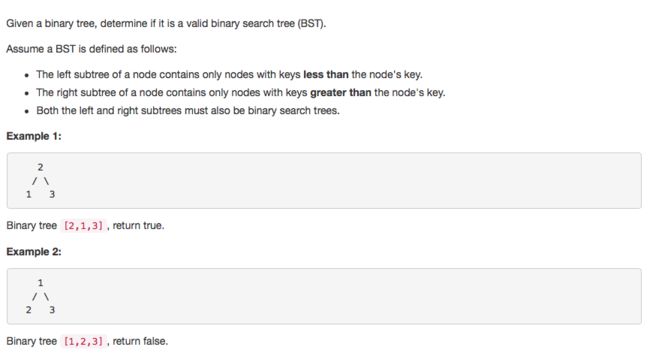
- lintcode 95.Validate Binary Search Tree, leetcode 98
- leetcode 437. Path Sum III --- 这题太好了!
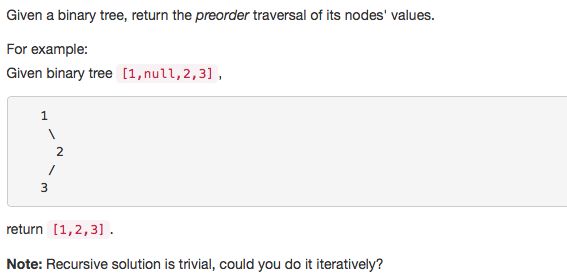
leetcode 144. Binary Tree Preorder Traversal (Iterative solution)
leetcode 145. Binary Tree Postorder Traversal (Iterative solution)
lintcode 67 Binary Tree Inorder Traversal (Iterative solution) 好题!
lintcode 97. Maximum Depth of Binary Tree
最简单的divide and conquer
package algorithm_ladder_IV;
/*
* 97. Maximum Depth of Binary Tree
*/
public class MaxDepthBST {
public int maxDepth(TreeNode root) {
if (root == null) return 0;
int left = maxDepth(root.left);
int right = maxDepth(root.right);
return 1 + Math.max(left, right);
}
}
lintcode 480. Binary Tree Paths, easy
package algorithm_ladder_IV;
import java.util.ArrayList;
import java.util.List;
public class BinaryTreePaths {
public List binaryTreePaths(TreeNode root) {
List res = new ArrayList();
if (root == null) return res;
// if leaf
if (root.left == null && root.right == null) {
res.add("" + root.val);
return res;
}
// if not leaf
List left = binaryTreePaths(root.left);
List right = binaryTreePaths(root.right);
for (String s : left)
res.add(root.val + "->" + s);
for (String s : right)
res.add(root.val + "->" + s);
return res;
}
}
lintcode 376.Binary Tree Path Sum
要点:divide and conquer 转化成子问题 (node, sum) -> (node.left, sum-node.val) & (node.right, sum-node.val)
解法1: classic divide and conquer
解法2: dfs 遍历
package algorithm_ladder_IV;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
/*
* leetcode 112
*/
public class PathSum {
public List> binaryTreePathSum(TreeNode root, int target) {
List> res = new ArrayList>();
// base case;
if (root == null) {
return res;
}
// is leaf
if (root.left == null && root.right == null) {
if (root.val == target) {
List p = new LinkedList();
p.add(root.val);
res.add(p);
}
return res;
}
// not leaf
List> left = binaryTreePathSum(root.left, target - root.val);
List> right = binaryTreePathSum(root.right, target - root.val);
for (List list : left) {
LinkedList l = new LinkedList<>(list);
l.addFirst(root.val);
res.add(l);
}
for (List list : right) {
LinkedList l = new LinkedList<>(list);
l.addFirst(root.val);
res.add(l);
}
return res;
}
}
要点: 注意dfs时 list.add 和 list.remove (对比permutation时 list的增减是在enumerate possible values时做的)。两者本质是一样的,只是看val是在什么时候放入list。
package algorithm_ladder_IV;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
/*
* Leetcode 112, alternative solution using dfs
*/
public class PathSumDFS {
private List> res;
public List> pathSum(TreeNode root, int sum) {
res = new ArrayList>();
List list = new LinkedList();
dfs(root, list, sum);
return res;
}
private void dfs(TreeNode root, List list, int sum) {
if (root == null) return;
list.add(root.val);
if (root.left == null && root.right == null) {
if (root.val == sum) {
res.add(new ArrayList(list));
}
} else {
dfs(root.left, list, sum-root.val);
dfs(root.right, list, sum-root.val);
}
list.remove(list.size()-1);
}
}
lintcode 596 Minimum Subtree
要点: 可以用ResultType,也可以用private field.
package algorithm_ladder_IV;
public class MinimumSubtree {
private int MinSum = Integer.MAX_VALUE;
private TreeNode ResNode = null;
public TreeNode findSubtree(TreeNode root) {
calSum(root);
return ResNode;
}
private int calSum(TreeNode root) {
if (root == null) return 0;
// not null
int left = calSum(root.left);
int right = calSum(root.right);
int newSum = left + right + root.val;
if (newSum < MinSum) {
MinSum = newSum;
ResNode = root;
}
return newSum;
}
}
lintcode 595.Binary Tree Longest Consecutive Sequence, leetcode 298
helper function在节点x只需要返回: 从节点x起始最长的连续序列。
Longest Consecutive Sequence 做field。
package algorithm_ladder_IV;
public class LongestConsecutiveSequence {
private int LCS = 0;
public int longestConsecutive(TreeNode root) {
currentLC(root);
return LCS;
}
// returns the length of from root node
private int currentLC(TreeNode root) {
if (root == null) return 0;
int leftLC = currentLC(root.left);
int rightLC = currentLC(root.right);
if (leftLC == 0) // root.left == null
leftLC = 1;
else { // root.left != null
if (root.val + 1 == root.left.val)
leftLC++;
else
leftLC = 1;
}
if (rightLC == 0) rightLC = 1;
else {
if (root.val+1 == root.right.val)
rightLC++;
else
rightLC = 1;
}
int currentLCS = Math.max(leftLC, rightLC);
if (currentLCS > LCS)
LCS = currentLCS;
return currentLCS;
}
}
leetcode 114 Flatten Binary Tree to Linked List, lintcode 453
要点: 二刷时写返回tail就可以了 -- head就是root.left, root.right;
package algorithm_ladder_IV;
public class FlattenBinaryTreeToLinkedList {
class ResultType {
TreeNode head;
TreeNode tail;
ResultType(TreeNode head, TreeNode tail) {
this.head = head;
this.tail = tail;
}
}
public void flatten(TreeNode root) {
flattenHelper(root);
}
private ResultType flattenHelper(TreeNode root) {
if (root == null) return new ResultType(null, null);
if (root.left == null && root.right == null) // leaf
return new ResultType(root, root);
// non-leaf node
ResultType left = flattenHelper(root.left);
ResultType right = flattenHelper(root.right);
if (left.head == null) { // left subtree is null
root.left = null;
root.right = right.head;
return new ResultType(root, right.tail); // right cannot be null
} else { // left subtree is non-null
root.left = null;
root.right = left.head;
left.tail.right = right.head;
TreeNode newTail = right.head == null ? left.tail : right.tail;
return new ResultType(root, newTail);
}
}
}
leetcode 236. Lowest Common Ancestor of a Binary Tree
要点1: 假设p,q都在binary tree里面的化, root == null || root == p || root == q 可以一起考虑。
要点2,如果p,q不在binary tree里面(此时返回null),则不能像要点1那样简单地做。需要有一个resultType{qFound, pFound}
package algorithm_ladder_IV;
public class LowestCommonAncestor {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root == null || root == p || root == q)
return root;
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
if (left == null && right == null)
return null;
else if (left == null)
return right;
else if (right == null)
return left;
else
return root;
}
/**
private TreeNode LCA = null;
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
findLCA(root, p, q);
return LCA;
}
public boolean findLCA(TreeNode root, TreeNode p, TreeNode q) {
if (root == null)
return false;
boolean left = findLCA(root.left, p, q);
boolean right = findLCA(root.right, p, q);
if (LCA != null) return true; // LCA found in subtrees
if (!left && !right) {
if (root == p || root == q) return true;
else return false;
}
if (left && right) {
LCA = root;
return true;
}
if ((root == p || root == q)
&& (left || right)) {
LCA = root;
return true;
} else
return true;
}
*/
}
lintcode 95.Validate Binary Search Tree, leetcode 98
题目不难,比较tricky, result type需要设成long,不然无法handle node.val = Integer.max_value的情况。
package algorithm_ladder_IV;
public class ValidateBinarySearchTree {
class ResultType{
long MinInBST;
long MaxInBST;
boolean isBST;
ResultType(long minInBST, long maxInBST, boolean isBST) {
super();
MinInBST = minInBST;
MaxInBST = maxInBST;
this.isBST = isBST;
}
}
public boolean isValidBST(TreeNode root) {
ResultType r = checkBST(root);
return r.isBST;
}
private ResultType checkBST(TreeNode root) {
if (root == null)
return new ResultType(Long.MAX_VALUE, Long.MIN_VALUE, true);
// 不需要讨论root是否是leaf
ResultType ltree = checkBST(root.left);
if (!ltree.isBST)
return new ResultType(Long.MAX_VALUE, Long.MIN_VALUE, false);
ResultType rtree = checkBST(root.right);
if (!rtree.isBST)
return new ResultType(Long.MAX_VALUE, Long.MIN_VALUE, false);
// both ltree and rtree are bst
if (ltree.MaxInBST < root.val && root.val < rtree.MinInBST)
// 注意左右子树为null的情况。
return new ResultType(Math.min(ltree.MinInBST, root.val), Math.max(root.val, rtree.MaxInBST), true);
else
return new ResultType(Integer.MAX_VALUE, Integer.MIN_VALUE, false);
}
}
leetcode 437. Path Sum III (好题!!!!)
笨办法是把所有的path都求出来然后一个一个地check (超时了)
递归,分治的好方法:
原问题:求满足条件的paths数
tree里满足条件的paths分成两类:
(1)从root开始的path ---- 这是一另一个问题(此问题也可以分治求解)。
(2) 左右子树中满足条件的paths (原问题的子问题)
//太经典了
public class PathSumIII_betterSolution {
public int pathSum(TreeNode root, int sum) {
if (root == null) return 0;
return pathSumFrom(root, sum) + pathSum(root.left, sum) + pathSum(root.right, sum);
}
private int pathSumFrom(TreeNode root, int sum) {
if (root == null) return 0;
return (root.val == sum ? 1:0) + pathSumFrom(root.left, sum-root.val) + pathSumFrom(root.right, sum-root.val);
}
}
我自己写了个笨办法:用一个ResultType包含了 1. 所有从node出发的paths 2. 非从node出发的paths
严重超时。
package algorithm_ladder_IV;
import java.util.ArrayList;
import java.util.LinkedList;
/*
* Leetcode 437
* Very similar to subsets
*/
public class PathSumIII {
class ResultType {
ArrayList> pathsFromCurrentNode;
ArrayList> pathsNotFromCurrentNode;
ResultType(ArrayList> pathsFromCurrentNode, ArrayList> pathsNotFromCurrentNode) {
this.pathsFromCurrentNode = pathsFromCurrentNode;
this.pathsNotFromCurrentNode = pathsNotFromCurrentNode;
}
}
private ArrayList> allPaths = new ArrayList>();
private int sum;
public int pathSum(TreeNode root, int sum) {
this.sum = sum;
ResultType r = findPaths(root);
for (LinkedList p : r.pathsFromCurrentNode) {checkPath(p);}
for (LinkedList p : r.pathsNotFromCurrentNode) {checkPath(p);}
printPaths(allPaths); // testing
return allPaths.size();
}
private ResultType findPaths(TreeNode root) {
ArrayList> pfcn = new ArrayList>();
ArrayList> pNfcn = new ArrayList>();
if (root == null) {
return new ResultType(pfcn, pNfcn);
}
ResultType left = findPaths(root.left);
ResultType right = findPaths(root.right);
for (LinkedList p : left.pathsFromCurrentNode) pNfcn.add(new LinkedList(p));
for (LinkedList p : left.pathsNotFromCurrentNode) pNfcn.add(new LinkedList(p));
for (LinkedList p : right.pathsFromCurrentNode) pNfcn.add(new LinkedList(p));
for (LinkedList p : right.pathsNotFromCurrentNode) pNfcn.add(new LinkedList(p));
for (LinkedList p : left.pathsFromCurrentNode) {
p.addFirst(root.val);
}
for (LinkedList p : right.pathsFromCurrentNode) {
p.addFirst(root.val);
}
pfcn.addAll(left.pathsFromCurrentNode);
pfcn.addAll(right.pathsFromCurrentNode);
LinkedList temp = new LinkedList(); temp.add(root.val);
pfcn.add(temp);
return new ResultType(pfcn, pNfcn);
}
private void checkPath(LinkedList path) {
int total = 0;
for (int i : path)
total += I;
if (total == sum)
allPaths.add(path);
}
private void printPaths(ArrayList> allPaths) {
for (LinkedList path: allPaths) {
for (int i : path) {
System.out.print(i + "->");
}
System.out.println("\n");
}
}
public static void main(String[] args) {
TreeNode root = new TreeNode(10);
TreeNode left = new TreeNode(5);
TreeNode right = new TreeNode(-3);
left.left = new TreeNode(3); left.right = new TreeNode(2);
left.left.left = new TreeNode(3); left.left.right = new TreeNode(-2);
left.right.right = new TreeNode(1);
right.right = new TreeNode(11);
root.left = left; root.right = right;
PathSumIII p = new PathSumIII();
System.out.println(p.pathSum(root, 1)); // should be 3
}
}
leetcode 144. Binary Tree Preorder Traversal (Iterative solution)
leetcode 145. Binary Tree Postorder Traversal
lintcode 67 Binary Tree Inorder Traversal
- recursive solution is trivial
- 用iteration解决recursive problem要用stack
- java doc推荐用
ArrayDeque, i.e.Deque;stack = ArrayDeque ()
- 要点:preorder最简单,inorder和postorder都有难度。
- preorder非递归很简单,有一个stack装treenode,每次pop出node的同时
a) 将node.val装入result中
b) 将right, left children分别push进栈 --- 先压入root.right 因为希望right后被处理。- inorder 和 postorder却不能如上处理,因为 a) 和 pop并不是同时完成的。
这就需要另外一个栈,来装在每个treenode的状态。
- 每个treenode的状态在NOT_DONE, LEFT_DONE, LEFT_RIGHT_DONE中转换
- 每次转换都依赖于对stack top的一次peek。只有当某个node状态变成LEFT_RIGHT_DONE才会有pop行为。
citation: (https://www.jianshu.com/p/8359c1369066)
public class BinaryTreeInorderTraversal {
static final int NOT_DONE = 0;
static final int LEFT_DONE = 1;
static final int LEFT_RIGHT_DONE = 2;
public List inorderTraversal(TreeNode root) {
LinkedList res = new LinkedList();
Deque stackNode = new ArrayDeque();
Deque stackState = new ArrayDeque();
if (root == null) return res;
stackNode.push(root);
stackState.push(NOT_DONE);
while (!stackNode.isEmpty()) {
TreeNode curNode = stackNode.peek();
int curState = stackState.peek();
if (curState == LEFT_DONE) { // condition for adding node to res.
res.add(curNode.val);
}
// 三种状态转换
if (curState == NOT_DONE) {
stackState.pop();
stackState.push(LEFT_DONE);
if (curNode.left != null) {
stackNode.push(curNode.left);
stackState.push(NOT_DONE);
}
} else if (curState == LEFT_DONE) {
// stackState.set(stackState.size() -1 , LEFT_RIGHT_DONE);
stackState.pop(); stackState.push(LEFT_RIGHT_DONE);
if (curNode.right != null) {
stackNode.push(curNode.right);
stackState.push(NOT_DONE);
}
} else if (curState == LEFT_RIGHT_DONE) {
stackNode.pop();
stackState.pop();
}
}
return res;
}
public static void main(String[] args) {
TreeNode root = new TreeNode(1);
root.right = new TreeNode(2);
root.right.left = new TreeNode(3);
root.left = new TreeNode(4);
BinaryTreeInorderTraversal b = new BinaryTreeInorderTraversal();
List list = b.inorderTraversal(root);
for (int i : list) System.out.print(i + " "); // should be 4 1 3 2
}
}