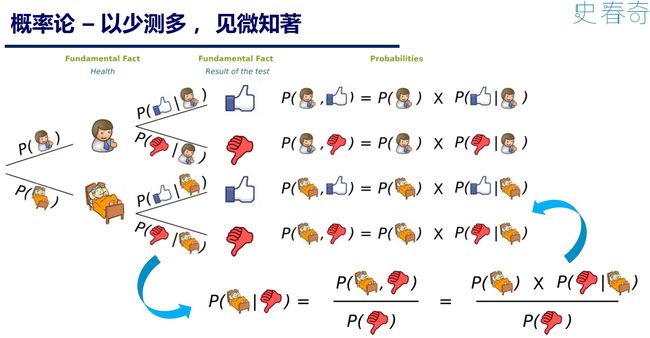
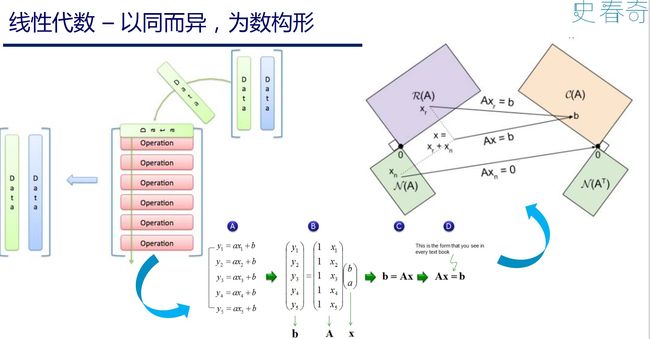
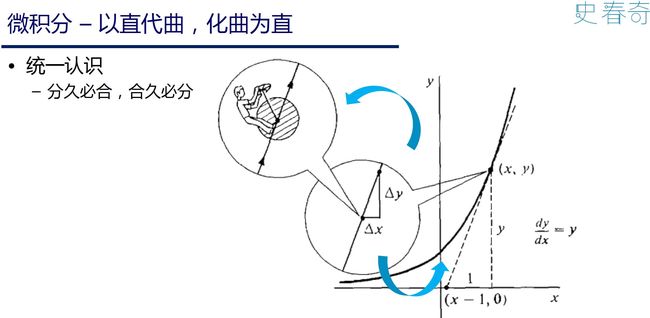
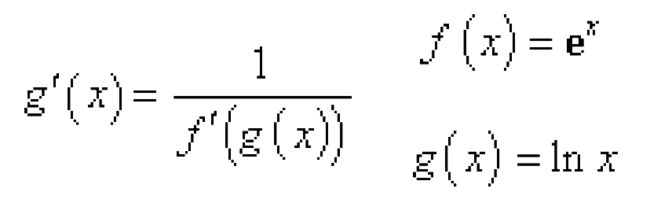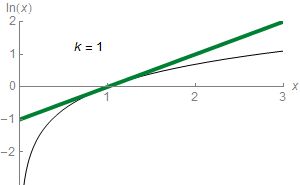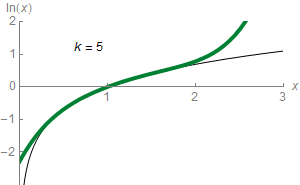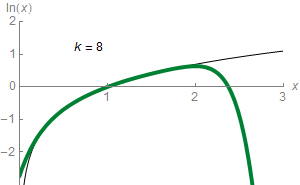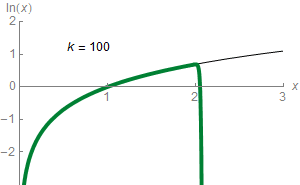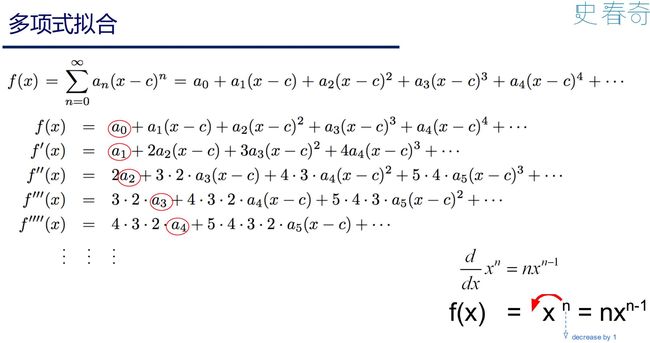要学好人工智能、机器学习、统计、 计量、量化、优化等等和统计相关的内容, 少不了三大块数学: 微积分、线性代数和概率统计。 前面我们在“概率分布の三奥义”里面探讨了概率统计的思路历程。 在“矩阵分解 (乘法篇)” 和 “矩阵分解 (加法篇)” 以及 “矩有四子” 讨论了代数空间的几何视角表示。 这里要讨论一下微积分的认知精神!
前言:
微积分在机器学习中最重要的作用之一是理论上阐明优化模型的正确性、可性性和高效性。 所以在这里, 会结合优化的部分,一起来描述‘化曲为直’是怎么改写认知的! 在这里,我们看一下, 有哪些直?
自由直线
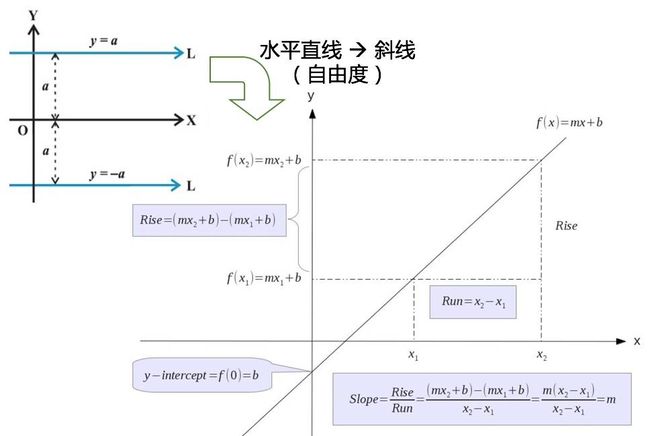
从水平直线到任意直线, 自由度的突破, 这个在高斯创建最小二乘法的时候就有高深的应用( 参考 ‘一步一步走向锥规划 - LS’)。 从水平直线, 到任意直线, 是自由的的增加。 从增加的角度来看直线的变化。
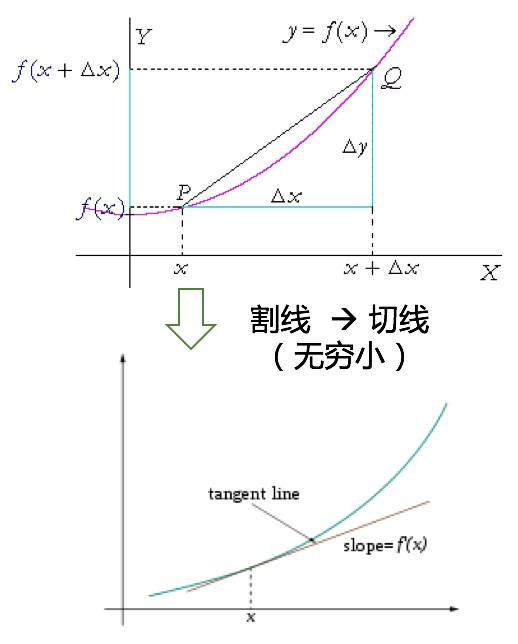
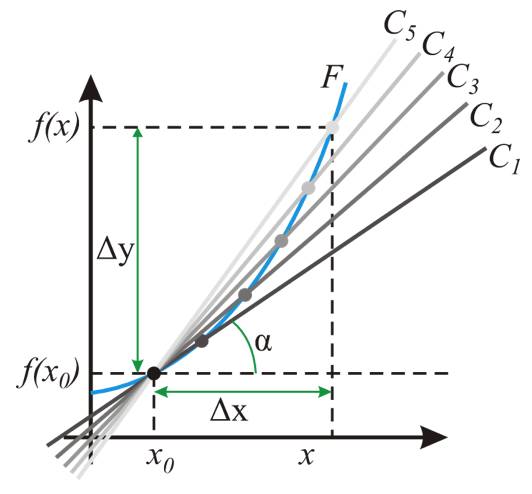
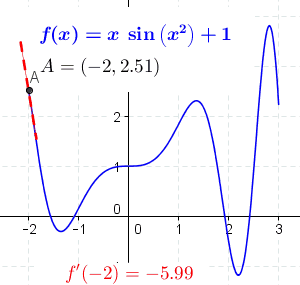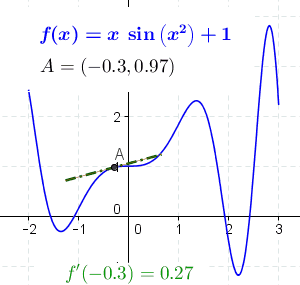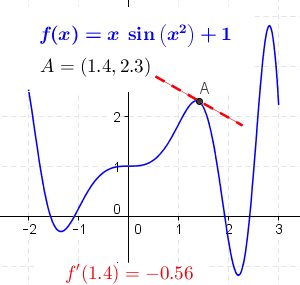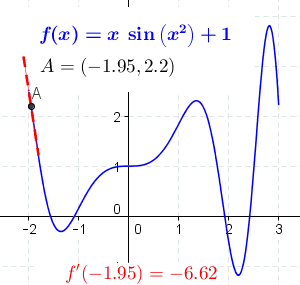
割线到切线
把光滑曲线的割线, 亮点无限靠近到两点之间的距离是无穷小的时候, 就产生了切线。 而这个无穷小,就是最早的导数思想的来源。
化曲为直第一式:以直代曲
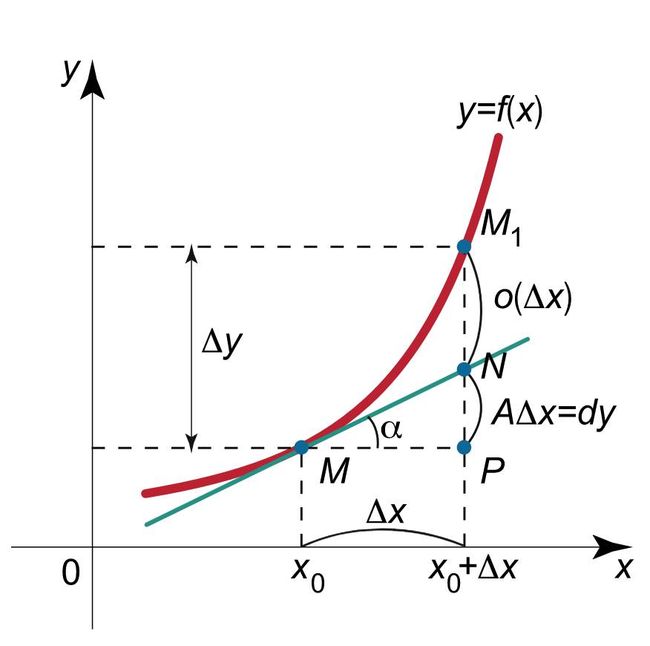
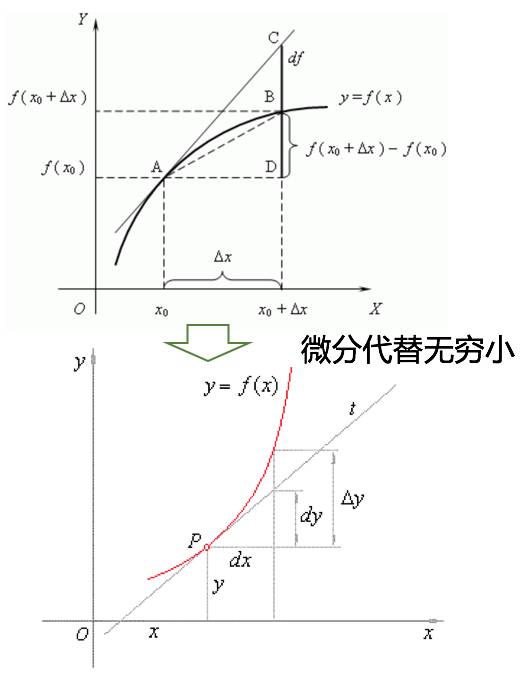
从导数到微分
在从无穷小到极限的完善过程中, 就建立起来导数,微分的思想。 通过极限的思想, 让无穷小变得可以比较。 类似可以划分高阶无穷小。
然后, 对微分的应用,就直接是用直线代替了曲线了, 以为更高阶的无穷小可以忽略。
化曲为直第二式:积直为曲
有了导数这个强大的工具之后, 我们可以得到导数的运算规则:
根据乘法规则, 我们知道可以给幂函数降阶。 根据链式规则, 我们可以计算反函数的导数。 有了反函数的导数计算, 我们又可以给幂函数的阶求倒数。
其实如果从图上看, 更为直观, 就是关于y=x直线对称。
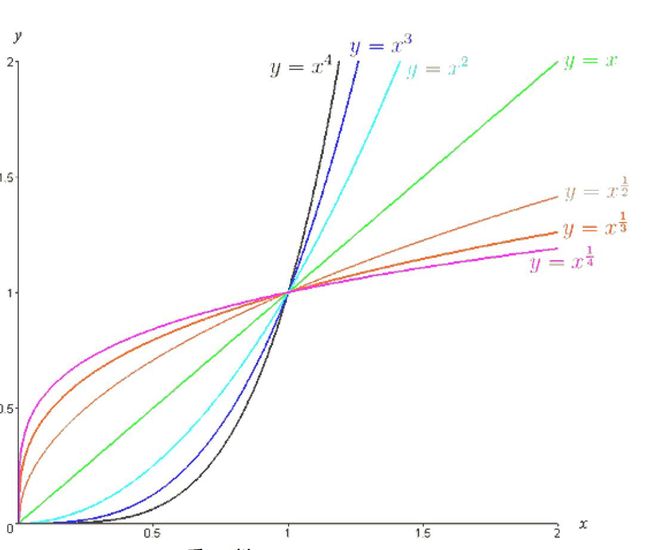
幂函数
有了降阶和求倒数, 所以常见幂函数的导数就差不多全了。 所以我们能通过导数这个工具, 把幂函数里面所有的曲线化成直线去看待。
所以, 通过以直代曲理解了导数工具, 通过导数工具,统一幂函数到直线。 求导的逆过程是积分, 所以相当于对直线的积分, 得到幂函数的曲线。
指数函数、对数函数和任意光滑函数
我们知道幂函数起源于对长度, 面积, 体积的认识。 而指数函数起源于对复利, 利滚利的认识。 而对数函数起源于对天文数字处理的认识。 这些基础函数的起源都很不一样。
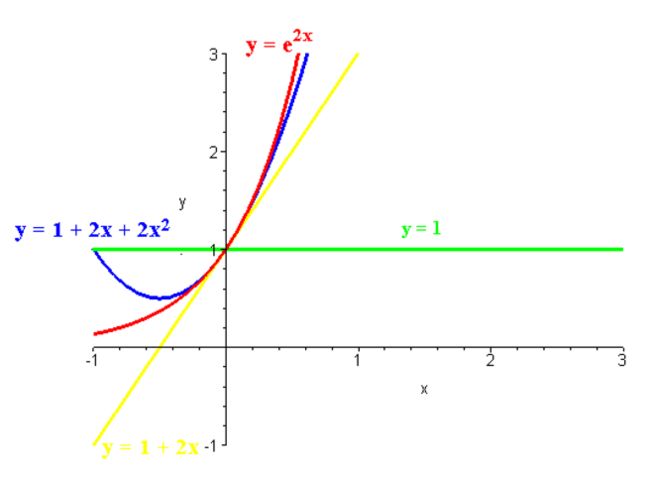
如何统一对函数的认识呢?人们想到了多项式函数拟合。 人们发现幂函数的加和可以模拟指数函数。
也可以逼近对数函数:
回头人们发现了, 这个多项式拟合的关键也是导数, 得出泰勒公式。
泰勒公式就是导数作用到多项式拟合上面, 对拟合系数的结论。
有了拟合系数的表达式, 那么任何光滑函数可以解释成幂函数的求和。 而前面我们又说了幂函数,可以解释成直线的求积。 所以某种意义上, 对直线进行各种求积, 然后再各种求和,就可以得到任何函数。
这样, 人们不仅仅做到了,积直为曲的过程, 而且改变了人们对函数的认识, 因为找到了直线作为任意曲线的共同基础, 导数、积分作为差异化的工具。人们开始考虑函数之间的距离和变化, 引发了泛函和变分法的思考 (参考 ‘变分の美’)。
化曲为直第三式:以直铭曲
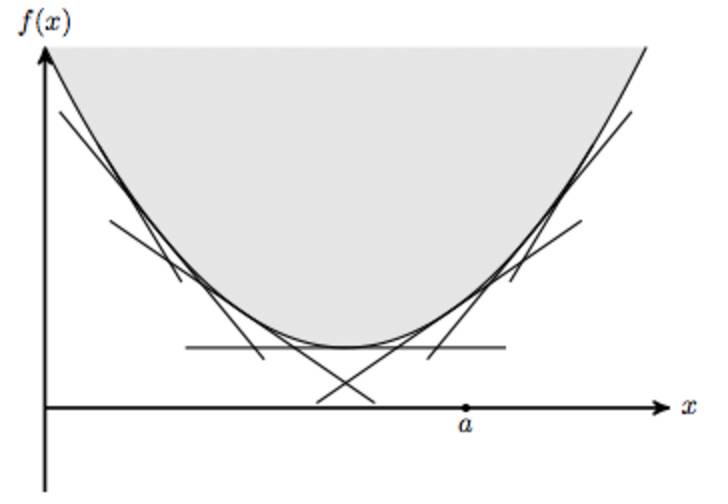
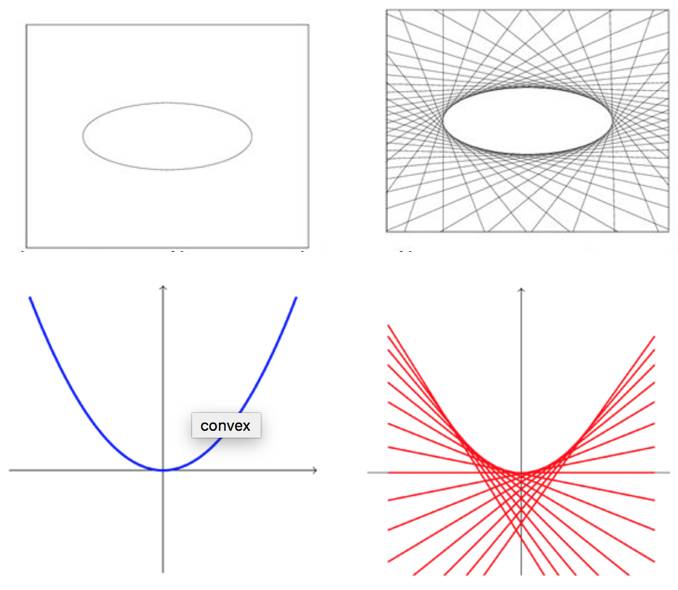
当我们把所有点的切线放在一起, 那么我们可以切出一条曲线来。
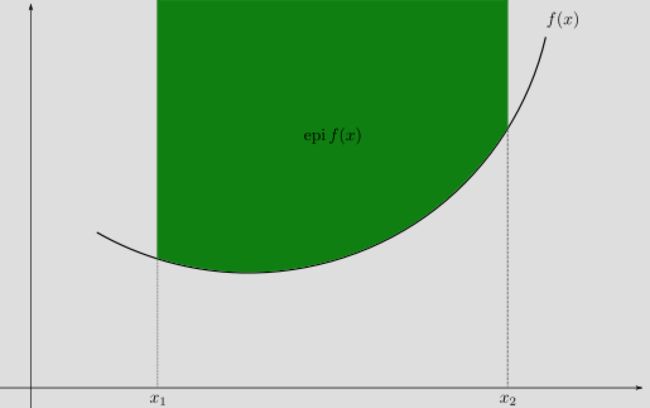
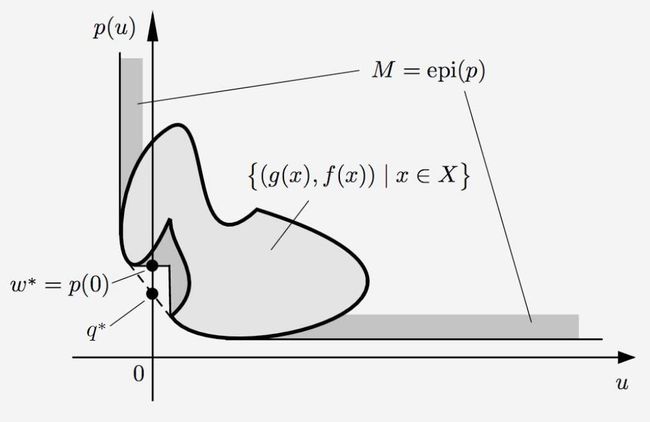
一般来说, 这个切出的曲线是铭图Epigraph的表面。 这个好比在石碑上刻图一样, 每次刻画都是直线, 但是慢慢的也能刻出各种凸面来。 所以这种从一条线的两边去看待同一个问题的方法叫共轭Conjugate。
这种思想, 有什么用呢? 这是最优化里面Fenchel共轭的基本思想。
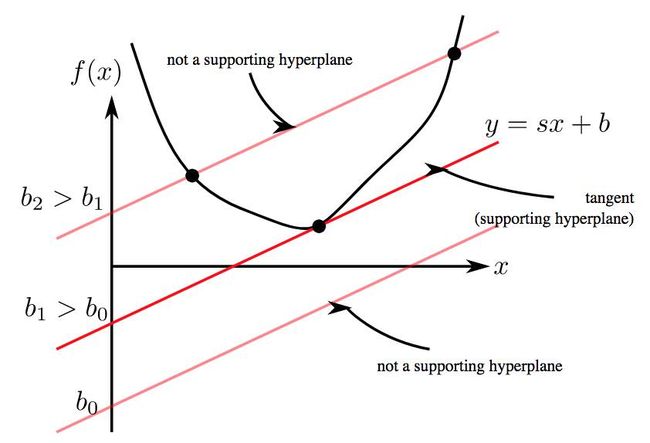
那么要确定一条直线, 需要知道斜率和截距。那么要知道一组切线的话, 我们根据, 引入自由度的情况,首先固定斜率, 这样就是一组平行线。 其中有部分割线的情况, 我们要知道固定斜率情况下的截距,使得是切线,只有一个交点。 所以我们得先找到斜率和截距之间的关系!
曲线切线斜率和截距之间的关系
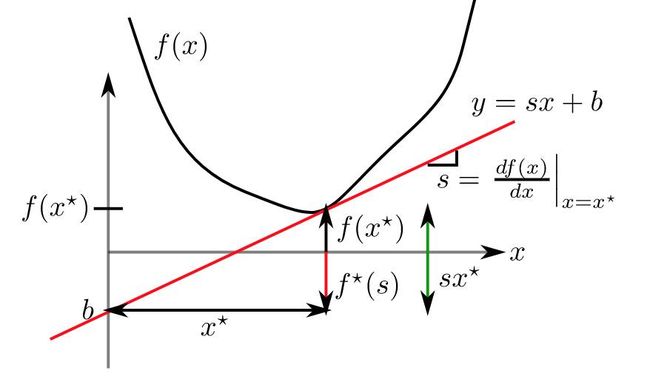
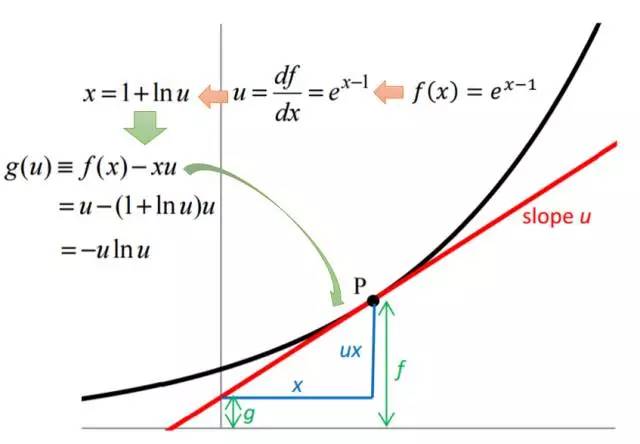
假设斜率s,那么固定s情况下, 经过一个切点( x*, f(x*) )的直线的截距和x*围成一个直角三角形。 这个直角三角形的斜率s为垂直边长度比上水平边长度的比值。或者说水平边长度乘以斜率得到垂直边长度。
这样我们找到了截距和斜率直接的关系, 在这个关系里面, 稍微有点不和谐的是负的斜率。 但是这样写成斜率的一阶形式,比较好看些。 那剩下来的问题, 只要确定这个切点就可以了。
Fenchel共轭
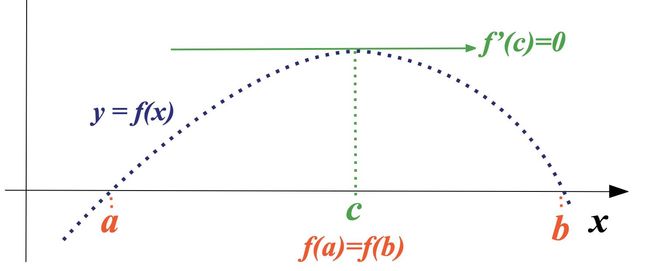
在Fenchel共轭里面切点, 不是直接表示为切线的交点, 而是间接的表示。 这是因为Fenchel共轭希望兼容不可导的情况。 扩大应用范围。 根据罗尔中值定理, 最值点的导数为0。
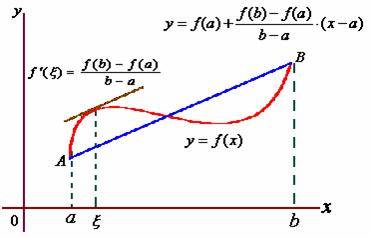
推广到拉格朗日中值定理,给定两点的最值点的切线。
然后Fenchel把这种最值和导数对应的关系用到了铭图的切线描述上。
所以, 我们通过一个最值变化, 引入上限来固定切点, 我们就得到-b关于斜率s的表达式了。换句话说, 一组切线可以知道了。
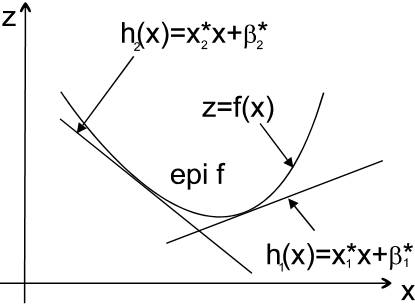
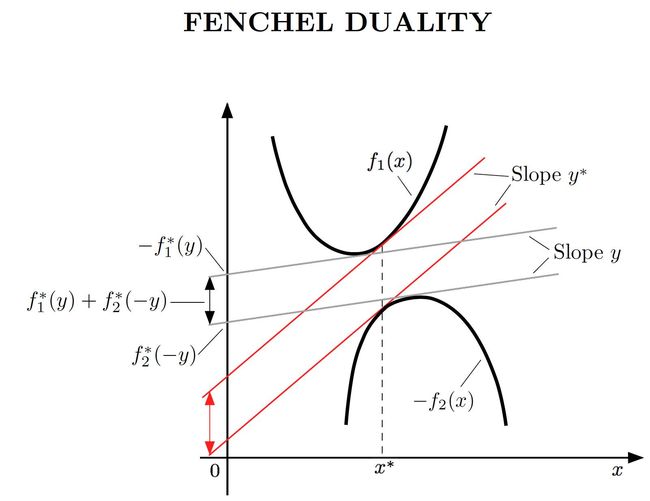
有了f(s)这个截距和斜率的关系式之后, 我们就可以知道任意的切线了。我们找一个斜率为x1*的, 先根据Fenchel共轭表达式计算-b1*,就可以固定h1(x)这个切线了。 同理可以固定h2(x)的切线。
有了Fenchel共轭的观点有什么好处呢?
假如不再把曲线看成了曲线, 而是看成游走的直线。
并且Fenchel共轭告诉了我们斜率和截距之间的关系, 我们能够找到对应的切线簇。
勒让德变换
其实上面讲的切线作为曲线支撑线簇的思想最早是Legendre提出来的 (参考:Legendre变变变)。 但是Legendre变换是完全建立在导数的基础上, 而不是建立在极值的基础上的。
但是, Fenchel对偶没有替换f(x)表达式, 而是利用极限取代导数。 这样可以兼容了不可导的点。 这也是subgradient扩展的一种情况。
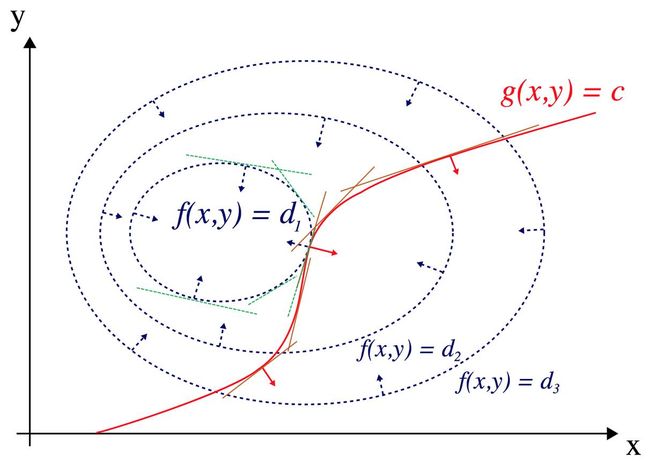
拉格朗日乘数法和对偶
有了Fenchel共轭的思想, 或者说Legendre变化的思想, 以直铭曲就成为新的强大工具。 可以解释Lagrange方法和对偶问题, Larange Duality 和 Fenchel Duality。
更为详细的内容参考 ‘走近中神通Fenchel’
小结:
本文从化直为曲的思想出发, 描述了以直代曲, 积直为曲, 以直铭曲三大思想, 分别对应到导数、泰勒公式、Fenchel共轭等方面知识。
分的角度:以直代曲, 分曲线为直线。
合的角度:泰勒公式 和 Fenchel共轭,积直线为曲线。
这些知识奠定了机器学习中, 微积分工具的基石。
相关话题:
概率分布の三奥义
变分の美
Legendre变变变
走近中神通Fenchel
矩阵分解 (乘法篇)
矩阵分解 (加法篇)
矩有四子
最大似然估计的2种论证
信息熵的由来
“66天写的逻辑回归” 引
一步一步走向锥规划 - LS
一挑三 FJ vs KKT
收敛率概述 (Overview of Rates of Convergence)
迭代优化算法之直观概述 (SVRG)
参考:
http://www.onmyphd.com/?p=legendre.fenchel.transform