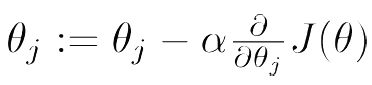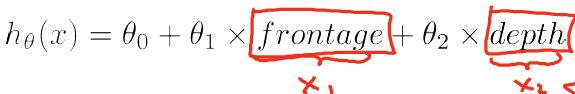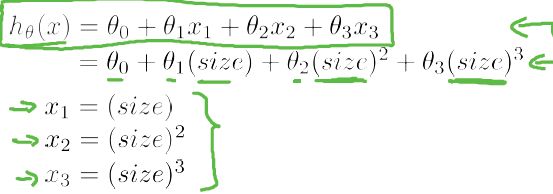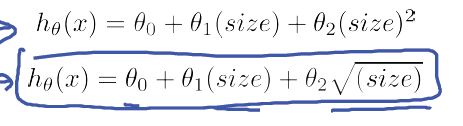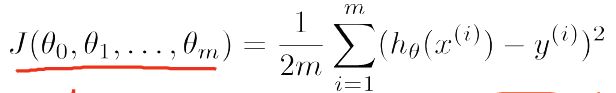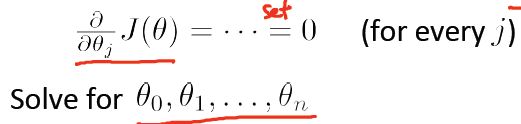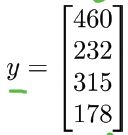章节5
原文链接
另一篇
https://www.coursera.org/learn/machine-learning/home/welcome
多变量线性回归主要包括以下部分:
1) Multiple features(多维特征)
2) Gradient descent for multiple variables(梯度下降在多变量线性回归中的应用)
3) Gradient descent in practice I: Feature Scaling(梯度下降实践1:特征归一化)
4) Gradient descent in practice II: Learning rate(梯度下降实践2:步长的选择)
5) Features and polynomial regression(特征及多项式回归)
6) Normal equation(正规方程-区别于迭代方法的直接解法)
7) Normal equation and non-invertibility (optional)(正规方程在矩阵不可逆情况下的解决方法)
1) Multiple features(多维特征)
第一课中我们谈到的是单变量的情况,单个特征的训练样本,单个特征的表达式,总结起来如下图所示:
对于多维特征或多个变量而言:以房价预测为例,特征除了“房屋大小外”,还可以增加“房间数、楼层数、房龄”等特征,如下所示:
定义:
n = 特征数目
x(i)= 第i个训练样本的所有输入特征,可以认为是一组特征向量
x(i)j= 第i个训练样本第j个特征的值,可以认为是特征向量中的第j个值
对于Hypothesis,不再是单个变量线性回归时的公式:hθ(x)=θ0+θ1x。
为了方便,记x0 = 1,则多变量线性回归可以记为:hθ(x)=θTx,其中θ和x都是向量。
2) Gradient descent for multiple variables(梯度下降在多变量线性回归中的应用)
梯度下降算法如下:
对J(θ)求导,分别对应的单变量和多变量梯度下降算法如下:
下图表示当特征数目为1,也就是n=1时。
当特征数目大于1也就是n>1时,梯度下降算法如下:
3) Gradient descent in practice I: Feature Scaling(梯度下降实践1:特征归一化)
核心思想:确保特征在相似的尺度里。
包含两种方式:
a. 简单的归一化
b. Mean Normalization(均值归一化):
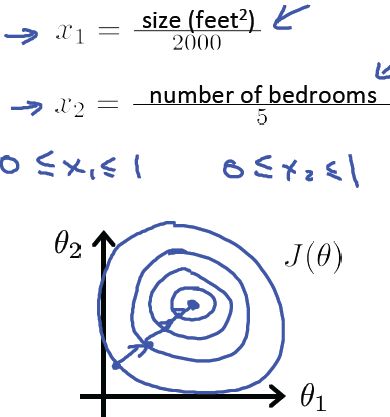
例如房价问题:
特征1:房屋的大小(0-2000);特征2:房间数目(1-5);
a. 简单的归一化
除以每组特征的最大值
目标:使每一个特征值都近似的落在−1≤xi≤1的范围内。
举例:因为是近似落在这个范围内,所以只要接近的范围基本上都可以接受,例如:
0<=x1<=3, -2<=x2<=0.5, -3 to 3, -1/3 to 1/3 都ok;
但是:-100 to 100, -0.0001 to 0.0001不Ok。
b. Mean Normalization(均值归一化):
用xi–μi替换xi使特征的均值近似为0(但是不对x0=1处理),均值归一化的公式是:xi=(xi–μi)/Si
其中μi是特征的平均值,Si可以是特征的取值范围(最大值-最小值),也可以是标准差(standard deviation).
对于房价问题中的两个特征,均值归一化的过程如下:
4) Gradient descent in practice II: Learning rate(梯度下降实践2:步长的选择)
对于梯度下降算法:
需要注意两点:
-“调试”:如何确保梯度下降算法正确的执行;
-如何选择正确的步长(learning rate):α;
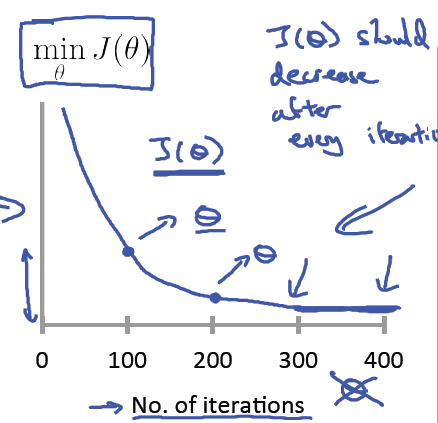
第二点很重要,它也是确保梯度下降收敛的关键点。要确保梯度下降算法正确运行,需要保证J(θ)在每一步迭代中都减小,如果某一步减少的值少于某个很小的值ϵ, 则其收敛。例如:
如果梯度下降算法不能正常运行,考虑使用更小的步长α,这里需要注意两点:
1)对于足够小的α,J(θ)能保证在每一步都减小;
2)但是如果α太小,梯度下降算法收敛的会很慢;
总结:
1)如果α太小,就会收敛很慢;
2)如果α太大,就不能保证每一次迭代J(θ)都减小,也就不能保证J(θ)收敛;
如何选择α-经验的方法:
…, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1…
约3倍于前一个数。
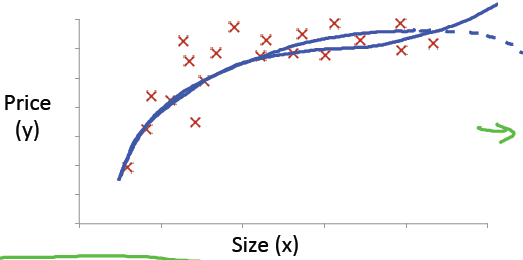
5) Features and polynomial regression(特征及多项式回归)
例子-房价预测问题:
特征x1表示frontage(正面的宽度),特征x2表示depth(深度)
同时x1,x2也可以用一个特征表示:面积 Area = frontage * depth
即hθ(x)=θ0+θ1x, x表示面积。
多项式回归:
很多时候,线性回归不能很好的拟合给定的样本点,例如:
所以我们选择多项式回归:
对于特征的选择,除了n次方外,也可以开根号,事实上也是1/2次方:
6) Normal equation(正规方程-区别于迭代方法的直接解法)
相对于梯度下降方法,Normal Equation是用分析的方法直接解决θ.
正规方程的背景:
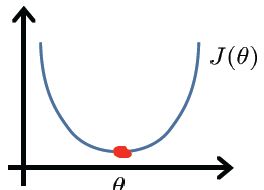
在微积分里,对于1维的情况,如果θ属于R:
J(θ)=aθ2+bθ+c
求其最小值的方法是令:
ddθJ(θ)=…=0
然后得到θ.
同理,在多变量线性回归中,对于θ∈Rn+1,Cost Function是:
求取θ的思路仍然是:
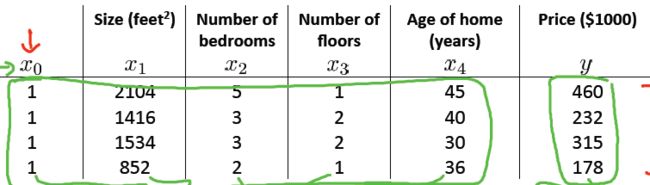
对于有4组特征(m=4)的房价预测问题:
其中X 是m * (n+1)矩阵:
y是m维向量:
则Normal equation的公式为:
θ=(XTX)−1XTy
注:这里直接给出了正规方程的公式,没有给出为什么是这样的,如果想知道原因,建议看看MIT线性代数第4章4.3节“最小二乘法”的相关内容,这里面最关键的一个点是:
“The partial derivatives of||Ax–b||2are zero whenATAx=ATb.
举例可见官方的PPT,此处略;
Octave公式非常简洁:pinv(X’ * X) * X’ * y
对于m个样本,n个特征的问题,以下是梯度下降和正规方程的优缺点:
梯度下降:
需要选择合适的learning rateα;
需要很多轮迭代;
但是即使n很大的时候效果也很好;
Normal Equation:
不需要选择α;
不需要迭代,一次搞定;
但是需要计算(XTX)−1,其时间复杂度是O(n3)
如果n很大,就非常慢
7) Normal equation and non-invertibility (optional)(正规方程在矩阵不可逆情况下的解决方法)
对于Normal Equation,如果XTX不可逆怎么办?
1) 去掉冗余的特征(线性相关):
例如以平方英尺为单位的面积x1, 和以平方米为单位的面积x2,其是线性相关的:
x1=(3.28)2x2
2) 过多的特征,例如m <= n:
删掉一些特征,或者使用regularization–之后的课程会专门介绍。