差分方程这名字大家可能不太熟悉,其实差分方程指的是下面这种:
其实就是我们数学中数列的递推公式,在以前学数学的时候,往往要通过递推公式来求通项公式才能快速地得到某一项的值,现在借助编程的话,仅仅有递推公式就足够生成一个数组了。
所以利用差分方程建模的关键在于如何得到第n组数据与第n+1组数据之间的关系。
实例1:培养皿中酵母菌数量的增长模型
生物工程专业的同学们可能接触过这样的试验,也画过这样的曲线。下面我们给不知道的同学们科普一下:
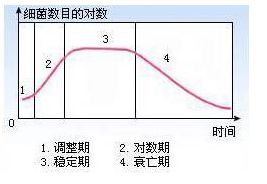
这个模型当然比之前的弹簧伸长模型要复杂一点。不知道大家还记不记得高中生物书上有一副这样的图:
如图所示我们用培养基培养细菌时,其数量变化通常会经历这四个时期。
而酵母菌因为生长周期长,我们经常能在小木虫或者丁香园上看见有人问:为何我的酵母菌培养了四五天还没有出现衰亡期啊??
在这个模型里面我们只针对前三个时期建一个大致的模型:调整期、对数期、稳定期。
数据分析
多说无益,我们先看数据:
| 时间 | 酵母菌数量 | 变化(Pn+1 - Pn) |
|---|---|---|
| 0 | 9.6 | 8.7 |
| 1 | 18.3 | 10.7 |
| 2 | 29 | 18.2 |
| 3 | 47.2 | 23.9 |
| 4 | 71.1 | 48 |
| 5 | 119.1 | 55.5 |
| 6 | 174.6 | 82.7 |
| 7 | 257.3 | 93.4 |
| 8 | 350.7 | 90.3 |
| 9 | 441.0 | 72.3 |
| 10 | 513.3 | 46.4 |
| 11 | 559.7 | 35.1 |
| 12 | 594.8 | 34.6 |
| 13 | 629.4 | 11.4 |
| 14 | 640.8 | 10.3 |
| 15 | 651.1 | 4.8 |
| 16 | 655.9 | 3.7 |
| 17 | 659.6 | 2.2 |
| 18 | 661.8 | --- |
根据以上数据我们可以很轻松的用Python画出酵母菌数量与时间和ΔP之间的关系的图形(详情请看上期推荐的matplotlib的简单教程)
import matplotlib.pyplot as plt
time = [i for i in range(0,19)]
number = [9.6,18.3,29,47.2,71.1,119.1,174.6,257.3,\
350.7,441.0,513.3,559.7,594.8,629.4,640.8,\
651.1,655.9,659.6,661.8]
plt.title('Relationship between time and number')#创建标题
plt.xlabel('time')#X轴标签
plt.ylabel('number')#Y轴标签
plt.plot(time,number)#画图
plt.show()#显示
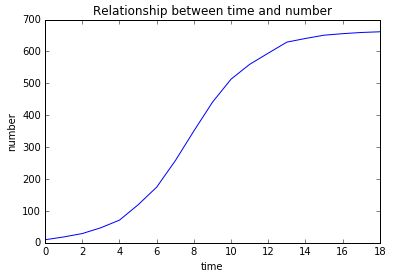
画出来的图是这样的(这个图是自己画的,第一期的是书本上的图)
尝试建模
这个图形看起来是不是很奇怪,这个模型的变化规律是什么呢?该如何建立这个模型呢,我们接下来分析一下:
1.强行拟合
对于这种模型我们当然也可以像上一期一样直接用numpy拟合,这个图形嘛,有点点像三次函数,我们可以试着用三次函数拟合一下试试,方法跟上期一样。
import numpy as np
import matplotlib.pyplot as plt
time = [i for i in range(0,19)]
number = [9.6,18.3,29,47.2,71.1,119.1,174.6,257.3,\
350.7,441.0,513.3,559.7,594.8,629.4,640.8,\
651.1,655.9,659.6,661.8]
f = np.polyfit(time,number,3)
y = np.polyval(f,time)#根据拟合之后的函数来求函数值
plt.plot(time,y,color = 'b')#根据函数值画图并设定颜色
plt.title('Relationship between time and number')
plt.xlabel('time')
plt.ylabel('number')
plt.plot(time,number,color = 'r')
plt.show()
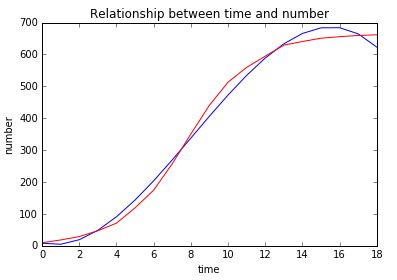
图形是这样的:
其中红色的原数据,蓝色是拟合之后的函数图像。
这种方法简单粗暴,在数据非常充足的时候是适用的,而在这个实例中我们要得到的是酵母菌数量随着时间变化的规律,主要拟合的话很难保证18h以后还能保持很好的拟合度。
这样拟合有个问题就是18小时之后的种群速度是会继续缓慢增长(抛物线形)还是逼近一个极限值(双曲线型)呢?
2.结合理论知识分析
数学建模即将实际问题转换为数学问题,这势必要了解实际问题的内部机理。
下面我们来对这个模型中的原理来分析一下,酵母菌培养是个很常见的实验,不了解的可以上网查查资料。
酵母菌数量增长有一个这样的规律:当某些资源只能支撑某个最大限度的种群数量,而不能支持种群数量的无限增长,当接近这个最大值时,种群数量的增长速度就会慢下来。
这个模型较为成熟的建立方式是通过差分方程来建立,我们来分析一下:
- 首先以两个观测点的值差Δp来表征增长速度。
- Δp与目前的种群数量有关,数量越大,增长速度越快。
- Δp还与剩余的未分配的资源量有关,资源越多,增长速度越快。
- 然后以极限总群数量与现有种群数量的差值来表征剩余资源量。
这样是不是模型是不是已经呼之欲出了(由表中猜测极限值是665,是多少都不重要)。
Δp = pn+1 - pn = k(665-pn)pn
公式中加了一个系数k,主要求出k值,这个模型就算完成了。
如何使用Python求系数k呢??
上面的式子中Δp和(665-pn)pn是不是成线性关系,我们只要根据数据求出二者的值,然后按上一期教程拟合一下,得到斜率就是我们所需要的k值了。
import numpy as np
pn = [9.6,18.3,29,47.2,71.1,119.1,174.6,\
257.3,350.7,441.0,513.3,559.7,594.8,629.4,\
640.8,651.1,655.9,659.6]
deltap = [8.7,10.7,18.2,23.9,48,55.5,\
82.7,93.4,90.3,72.3,46.4,35.1,\
34.6,11.4,10.3,4.8,3.7,2.2]
pn = np.array(pn)
factor = pn*(665-pn)
f = np.polyfit(factor,deltap,1)
print(f)
输出结果是这样的,前一个是系数,后一个是截距。
0.00081448 -0.30791574
至此,酵母菌这个模型就讲解完毕了,方程是:
Δp = pn+1 - pn = 0.00081448(665-pn)pn
拟合后的图形就不用画了吧,按前面讲的方法自己画一画,很简单的。
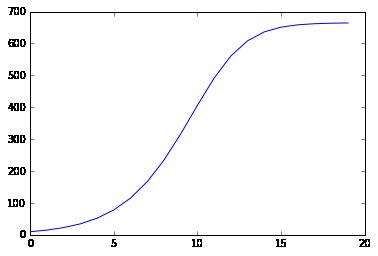
@乡土老农 问到这个图像怎么画,代码是这样的:
import matplotlib.pyplot as plt
p0 = 9.6
p_list = []
for i in range(20):
p_list.append(p0)
p0 = 0.00081448*(665-p0)*p0+p0
plt.plot(p_list)
plt.show()
有兴趣转行机器学习的朋友可以加群: