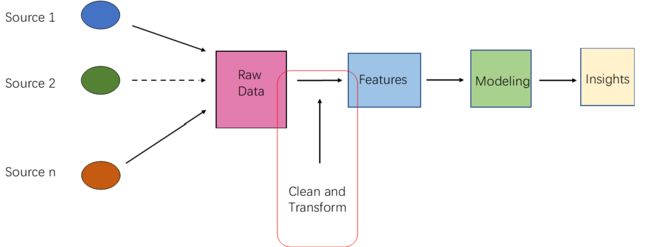
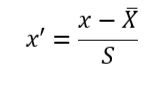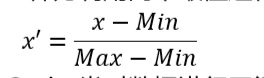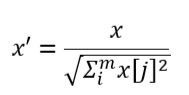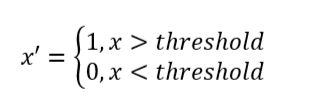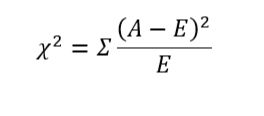1.特征工程是什么?
特征工程就是通过X,创造新的X'。顾名思义,其本质是一项工程活动,目的是最大限度地从原始数据中提取特征以供算法和模型使用。
一个非常简单的例子,现在出一非常简答的二分类问题题,请你使用逻辑回归,设计一个身材分类器。输入数据X:身高和体重 ,标签为Y:身材等级(胖,不胖)。显然,不能单纯的根据体重来判断一个人胖不胖,姚明很重,他胖吗?显然不是。针对这个问题,一个非常经典的特征工程是,BMI指数,BMI=体重/(身高^2)。这样,通过BMI指数,就能非常显然地帮助我们,刻画一个人身材如何。甚至,你可以抛弃原始的体重和身高数据。
2.特征工程过程
2.1 数据采集/清洗/采样
2.1.1 数据采集
2.1.2 数据清洗——清洗异常样本
数据清洗是很重要的一步,机器学习算法大多数时候就是一个加工机器,至于最后的产品如何,取决于原材料的好坏。数据清洗就是要去除异常样本。
那么如何判定异常样本呢?
1)简单属性判定:一个人身高3米+的人;一个人一个月买了10w的发卡
2)组合或统计属性判定:号称在米国却IP一直都是大陆的新闻阅读用户;你要判定一个人是否会买篮球鞋,样本中女性用户85%?
3)采用异常点检测算法:
偏差检测:聚类、最近邻等。用聚类方式划分数据为不同的簇,计算簇内每个点对于簇中心的相对距离(相对距离= 点到簇中心的距离/这个簇所有点到簇中心距离的中位数),可视化后,检测出相对距离较大的点。
基于统计的异常点检测:例如极差,四分位数间距,均差,标准差等
基于距离的异常点检测:与大多数点之间距离大于某个阈值的点视为异常点
基于密度的异常点检测:考察当前点周围密度,可以发现局部异常点
2.1.3 数据采样
采集、清洗过数据以后,正负样本是不均衡的,要进行数据采样。采样的方法有随机采样和分层抽样。但是随机采样会有隐患,因为可能某次随机采样得到的数据很不均匀,更多的是根据特征采用分层抽样。
正负样本不平衡处理办法:
正样本>> 负样本,且量都挺大 => downsampling
正样本>> 负样本,量不大 => 1)采集更多的数据
2)oversampling(比如图像识别中的镜像和旋转)
3)修改损失函数/loss function (设置样本权重)
损失函数用来评价模型的预测值和真实值不一样的程度,损失函数越好,通常模型的性能越好。
如在疾病筛查中,通常来讲正例比较少,负例比较多,有病的占少数而绝大部分人是健康的,这种数量不均衡的数据可能会让分类器倾向于将所有的示例都分为健康人,因为这样整体的准确率可能就能达到90%以上,为此,可以用调整loss权重的方式来缓解样本数量不均衡的问题,通过给病人的损失项乘了一个较大的系数,使得一旦占少数的病人被错分为健康人的时候,代价就非常的大。同样的给正常人的损失项乘了一个较小的系数,使其诊断错误时对网络的影响较小。这也符合实际情况,即使健康人在筛查时被通知可能患病,只要再进一步检查就可以。但是如果在筛查的时候将病人误分为健康人,那么付出的就可能是生命的代价了。
2.2 数据预处理
通过以上过程,我们能得到未经处理的特征,这时的特征可能有以下问题:
不属于同一量纲:即特征的规格不一样,不能够放在一起比较。无量纲化可以解决这一问题。
信息冗余:对于某些定量特征,其包含的有效信息为区间划分,例如学习成绩,假若只关心“及格”或不“及格”,那么需要将定量的考分,转换成“1”和“0”表示及格和未及格。二值化可以解决这一问题。
定性特征不能直接使用:某些机器学习算法和模型只能接受定量特征的输入,那么需要将定性特征转换为定量特征。最简单的方式是为每一种定性值指定一个定量值,但是这种方式过于灵活,增加了调参的工作。通常使用哑编码的方式将定性特征转换为定量特征:假设有N种定性值,则将这一个特征扩展为N种特征,当原始特征值为第i种定性值时,第i个扩展特征赋值为1,其他扩展特征赋值为0。哑编码的方式相比直接指定的方式,不用增加调参的工作,对于线性模型来说,使用哑编码后的特征可达到非线性的效果。
存在缺失值:缺失值需要补充。
信息利用率低:不同的机器学习算法和模型对数据中信息的利用是不同的,之前提到在线性模型中,使用对定性特征哑编码可以达到非线性的效果。类似地,对定量变量多项式化,或者进行其他的转换,都能达到非线性的效果。
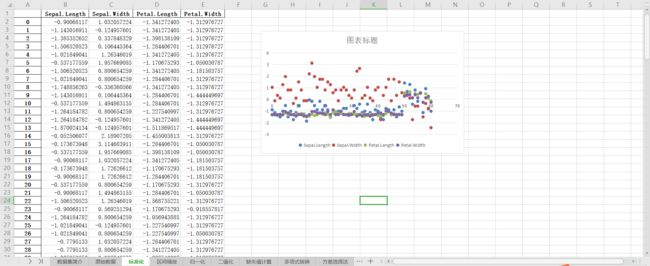
使用sklearn中的preproccessing库来进行数据预处理,可以覆盖以上问题的解决方案。本文使用sklearn中的IRIS(鸢尾花)数据集来对特征处理功能进行说明。以下是原始数据集:
2.2.1 无量纲化
2.2.1.1 标准化
标准化需要计算特征的均值和标准差,公式表达为:
使用preproccessing库的StandardScaler类对数据进行标准化,附输出结果
2.2.1.2 区间缩放法
区间缩放法的思路有多种,常见的一种为利用两个最值进行缩放,公式表达为:
使用preproccessing库的MinMaxScaler类对数据进行区间缩放的代码如下,附输出结果
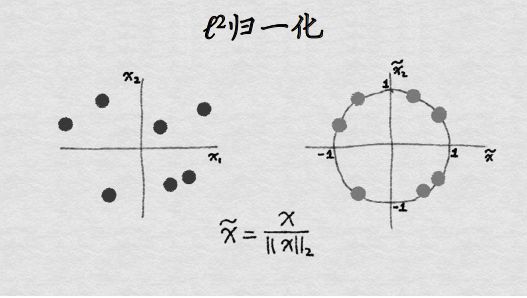
2.2.1.3 归一化
归一化是依照特征矩阵的行处理数据,其目的在于样本向量在点乘运算或其他核函数计算相似性时,拥有统一的标准,也就是说都转化为“单位向量”。规则为L2的归一化公式如下:
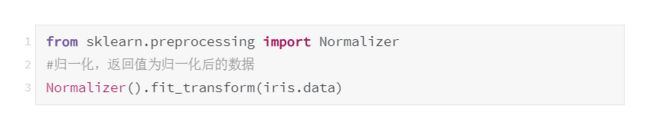
使用preproccessing库的Normalizer类对数据进行归一化的代码如下,附输出结果
2.2.2 对定量特征二值化
定量特征二值化的核心在于设定一个阈值,大于阈值的赋值为1,小于等于阈值的赋值为0,公式表达如下:
使用preproccessing库的Binarizer类对数据进行二值化的代码如下,附输出结果
2.2.3 对定性特征哑编码
由于IRIS数据集的特征皆为定量特征,故使用其目标值进行哑编码(实际上是不需要的)。使用preproccessing库的OneHotEncoder类对数据进行哑编码的代码如下,附输出结果
2.2.4 缺失值计算
由于IRIS数据集没有缺失值,故对数据集新增一个样本,4个特征均赋值为NaN,表示数据缺失。使用preproccessing库的Imputer类对数据进行缺失值计算的代码如下,附输出结果
2.2.5 数据变换
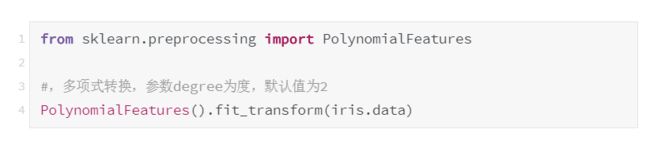
常见的数据变换有基于多项式的、基于指数函数的、基于对数函数的。4个特征,度为2的多项式转换公式如下:
使用preproccessing库的PolynomialFeatures类对数据进行多项式转换的代码如下,附输出结果
基于单变元函数的数据变换可以使用一个统一的方式完成,如使用preproccessing库的FunctionTransformer对数据进行对数函数转换。
2.3 特征选择
当数据预处理完成后,我们需要选择有意义的特征输入机器学习的算法和模型进行训练。通常来说,从两个方面考虑来选择特征:
特征是否发散:如果一个特征不发散,例如方差接近于0,也就是说样本在这个特征上基本上没有差异,这个特征对于样本的区分并没有什么用。
特征与目标的相关性:这点比较显见,与目标相关性高的特征,应当优选选择。除方差法外,本文介绍的其他方法均从相关性考虑。
根据特征选择的形式又可以将特征选择方法分为3种:
Filter:过滤法,按照发散性或者相关性对各个特征进行评分,设定阈值或者待选择阈值的个数,选择特征。
Wrapper:包装法,根据目标函数(通常是预测效果评分),每次选择若干特征,或者排除若干特征。
Embedded:嵌入法,先使用某些机器学习的算法和模型进行训练,得到各个特征的权值系数,根据系数从大到小选择特征。类似于Filter方法,但是是通过训练来确定特征的优劣。
使用sklearn中的feature_selection库来进行特征选择。
2.3.1 Filter
2.3.1.1 方差选择法
使用方差选择法,先要计算各个特征的方差,然后根据阈值,选择方差大于阈值的特征。使用feature_selection库的VarianceThreshold类来选择特征的代码如下,附输出结果
2.3.1.2 相关系数法
使用相关系数法,先要计算各个特征对目标值的相关系数以及相关系数的P值。用feature_selection库的SelectKBest类结合相关系数来选择特征的代码如下,附输出结果
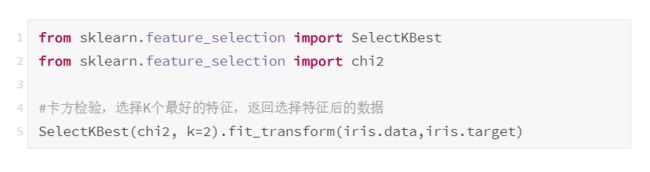
2.3.1.3 卡方检验
经典的卡方检验是检验定性自变量对定性因变量的相关性。假设自变量有N种取值,因变量有M种取值,考虑自变量等于i且因变量等于j的样本频数的观察值与期望的差距,构建统计量:
这个统计量的含义简而言之就是自变量对因变量的相关性。用feature_selection库的SelectKBest类结合卡方检验来选择特征的代码如下,附输出结果
2.3.1.4 互信息法
经典的互信息也是评价定性自变量对定性因变量的相关性的,互信息计算公式如下:
为了处理定量数据,最大信息系数法被提出,使用feature_selection库的SelectKBest类结合最大信息系数法来选择特征的代码如下,附输出结果
2.3.2 Wrapper
2.3.2.1 递归消除特征
递归消除特征法使用一个基模型来进行多轮训练,每轮训练后,消除若干权值系数的特征,再基于新的特征集进行下一轮训练。使用feature_selection库的RFE类来选择特征的代码如下,附输出结果
2.3.3 Embedded
2.3.3.1 基于惩罚项的特征选择法
使用带惩罚项的基模型,除了筛选出特征外,同时也进行了降维。使用feature_selection库的SelectFromModel类结合带L1惩罚项的逻辑回归模型,来选择特征的代码如下,附输出结果
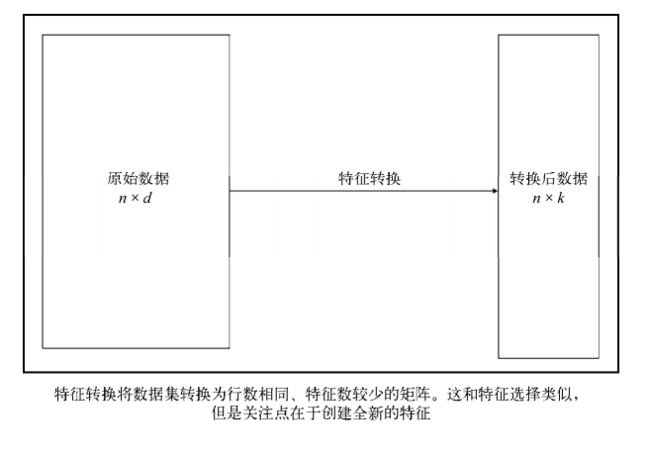
2.4 降维
当特征选择完成后,可以直接训练模型了,但是可能由于特征矩阵过大,导致计算量大,训练时间长的问题,因此降低特征矩阵维度也是必不可少的。常见的降维方法除了以上提到的基于L1惩罚项的模型以外,另外还有主成分分析法(PCA)和线性判别分析(LDA),线性判别分析本身也是一个分类模型。PCA和LDA有很多的相似点,其本质是要将原始的样本映射到维度更低的样本空间中,但是PCA和LDA的映射目标不一样:PCA是为了让映射后的样本具有最大的发散性;而LDA是为了让映射后的样本有最好的分类性能。所以说PCA是一种无监督的降维方法,而LDA是一种有监督的降维方法。
2.4.1 主成分分析法(PCA)
主成分分析(PCA,principal components analysis)是将有多个相关特征的数据集投影到相关特征较少的坐标系上。这些新的、不相关的特征(之前称为超级列)叫主成分。主成分能替代原始特征空间的坐标系,需要的特征少、捕捉的变化多。
主成分会产生新的特征,最大化数据的方差。这样,每个特征都会解释数据的形状。主成分按可以解释的方差来排序,第一个主成分最能解释数据的方差,第二个其次。
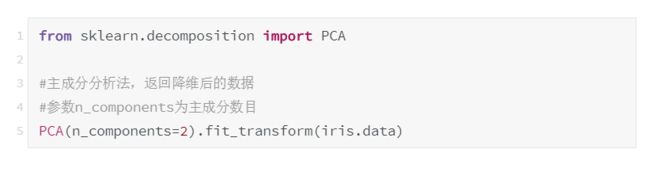
使用decomposition库的PCA类选择特征的代码如下,附输出结果
2.4.2 线性判别分析法(LDA)
LDA的全称是Linear Discriminant Analysis(线性判别0分析),是一种有监督学习算法。
LDA的原理是,将带上标签的数据(点),通过投影的方法,投影到维度更低的空间中,使得投影后的点,会形成按类别区分,一簇一簇的情况,相同类别的点,将会在投影后的空间中更接近。用一句话概括就是:“投影后类内方差最小,类间方差最大”
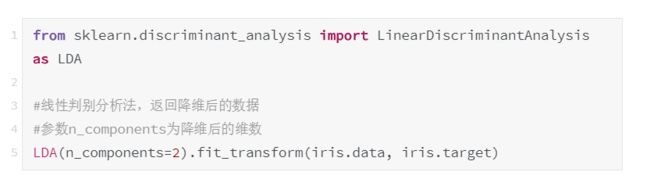
使用lda库的LDA类选择特征的代码如下,附输出结果