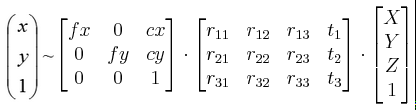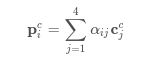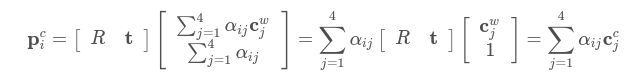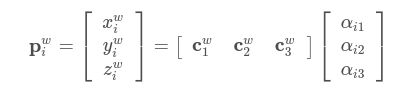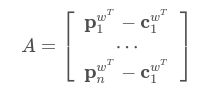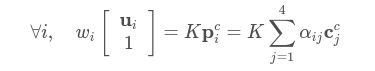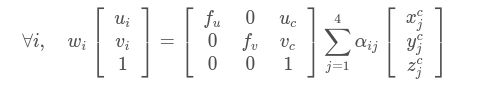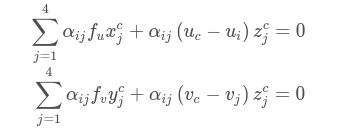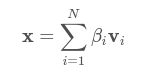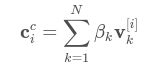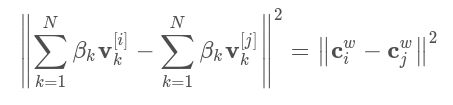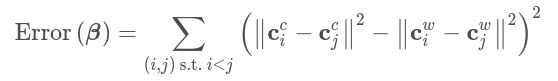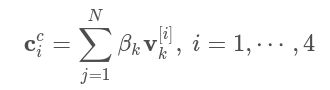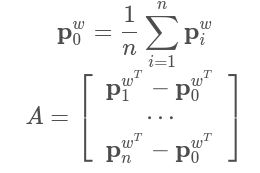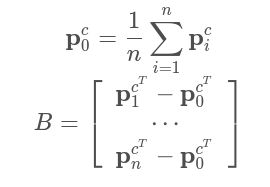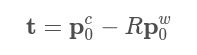本博客内容来源于网络以及其他书籍,结合自己学习的心得进行重编辑,因为看了很多文章不便一一标注引用,如图片文字等侵权,请告知删除。
学习笔记目录----->传送门 <-----
PNP问题简介
PNP问题的描述以及定义是相对简单的,他的目的就是求解3D-2D点对运动的方法。简单来说,就是在已知n个三维空间点坐标(相对于某个指定的坐标系A)及其二维投影位置的情况下,如何估计相机的位姿(即相机在坐标系A下的姿态)。举个例子,我们在一幅图像中,知道其中至少四个图像中确定的点在3D空间下的相对坐标位置,我们就可以估计出相机相对于这些点的姿态,或者说估计出这些3D点在相机坐标系下姿态。(上述说的姿态或者位姿,包括位置以及方向,即一个6自由度的状态)
PNP问题的可解性
从上面的问题简介中,我们可以了解到整个问题比较清晰,那么该怎么求解呢?虽然前面定义说明了在已知4对点对的情况下,是可以求出问题的解,但是在了解怎么求解前,我们应该先了解这个问题是不是真的有解?这将有助于我们理解下面的PNP问题的求解方法。
在分析PNP问题的可解性之前,应该需要知道小孔相机的参数模型,后续会在我的其他文章中给出。
1. 当PNP中N=1时,即只知道一对3D-2D点对的情况下:
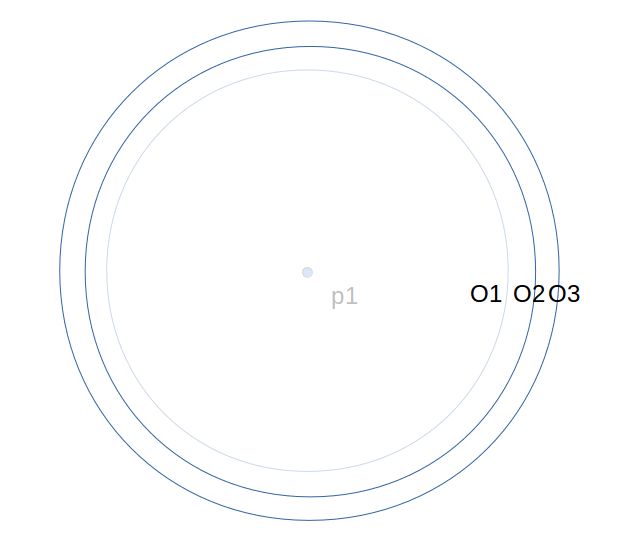
当只有一个特征点P1,我们假设它就在图像的正中央,那么显然向量OcP1就是相机坐标系中的Z轴,此事相机永远是面对P1,于是相机可能的位置就是在以P1为球心的球面上,再一个就是球的半径也无法确定,于是有无数个解。
如上图(2D示意图)的示例,Oc有可能在O1球上的任何一点,或者O2或O3球上的任何一点。
2. 当PNP中N=2时,即只知道两对3D-2D点对的情况下:
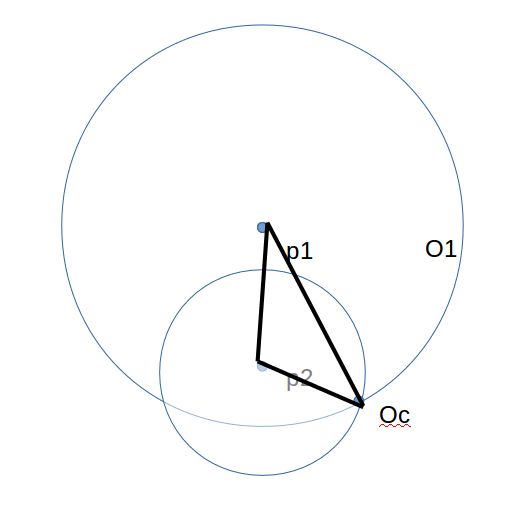
现在多了一个约束条件,显然OcP1P2形成一个三角形,由于P1、P2两点位置确定,三角形的边P1P2确定,再加上向量OcP1,OcP2,根据小孔模型,从Oc点射线特征点的方向角也能确定,于是能够计算出OcP1的长度=r1,OcP2的长度=r2。于是这种情况下得到两个球:以P1为球心,半径为r1的球A;以P2为球心,半径为r2的球B。显然,相机位于球A,球B的相交处,应该是一个圆圈,依旧是无数个解。
3. 当PNP中N=3时,即只知道三对3D-2D点对的情况下:
与上述相似,这次又多了一个以P3为球心的球C,相机这次位于ABC三个球面的相交处,终于不再是无数个解了,但是这次应该会有4个解,其中一个就是我们需要的真解了。
4. 当PNP中N>3时,即知道三对以上3D-2D点对的情况下:
N=3时求出4组解,对于一般的方程组再加一组数据就可以解决问题,事实上也几乎如此。这里还有其他一些特殊情况,这些特殊情况就比较复杂了,暂不详解。我们就可以认定,N>3后,能够求出正解了。但当直接使用4个点时,由于精度误差,并不能直接接触精确解,而是先用3个点计算出4组解获得四个旋转矩阵、平移矩阵。根据公式:
将第四个点的世界坐标代入公式,获得其在图像中的四个投影(一个解对应一个投影),取出其中投影误差最小的那个解,就是我们所需要的正解。
至此,我们就能确定在我们有至少4个点时,就PNP问题就可以结算出一个相对正确的解。
PNP问题求解方法
PNP 的问题是一致的,不同的就是在已知3D-2D的点对的情况下,怎么求出相机的位姿或者说点对在相机坐标系下的姿态。常见的PNP问题的求解方法,有以下几种:
- 直接线性变换DLT
- EPnP
- SDP
- P3P
- UPnP
- 非线性优化方法等……
下面我们来一一详细的解释其中几种方法求解的思路和过程,其中EPNP详解,其他方法简要介绍思路。
PNP 问题EPNP解法详解
有关EPNP的解释,主要是从文章深入EPnP算法学习而来,下面文字主要来自这篇博客,并进行重新排版。(就是感觉CSDN上广告太多了,导致排版不清晰)
算法的大概思路如下:
利用已知的3d点,通过PCA选择4个控制点,建立新的局部坐标系,从而将3d坐标用新的控制点表示出来。然后,利用相机投影模型和2d点,转换到相机坐标系中,再在相机坐标系中建立和世界坐标系同样关系(每个点在相机坐标系和世界坐标系下控制点处的坐标一致)的4个控制点,求解出相机坐标系下的四个控制点的坐标,进而利用ICP求解pose。(先有个初步印象,具体一些概念,我们接下来看公式慢慢理解)。
控制点和重心坐标系
本文中分别用上标w和c表示在世界坐标系和摄像头坐标系中的坐标,那么,3D参考点在世界坐标系中的坐标为pwi, i=1,⋯,n,在摄像头参考坐标系中的坐标为pci, i=1,⋯,n。4个控制点在世界坐标系中的坐标为cwj, j=1,⋯,4,在摄像头参考坐标系中的坐标为ccj, j=1,⋯,4。需要指出,在本文中,pwi,pci,cwj,ccj均非齐次坐标。(Markdown怎么写公式呢????)
EPnP算法将参考点的坐标表示为控制点坐标的加权和:
其中αij是齐次barycentric坐标。一旦虚拟控制点确定后,且满足4个控制点不共面的前提,aij,j=1,⋯,4是唯一确定的。在摄像头坐标系中,存在同样的加权和关系:推导如下:
在上述推导过程中,用到了EPnP对权重αij 加和为1的约束条件,如果没有这个条件则不成立。
那么问题来了:在一般的情形下,为什么需要4个控制点?要知道pwi 是非齐次的3D坐标,pwi∈ℝ3 ,为什么3个控制点就不可以呢?
这样我们就可以得出精确解。本质上就是:3D参考点的齐次坐标是控制点齐次坐标的线性组合。从而我们可以得出重心坐标系的计算方法:
控制点的选择
原则上,只要控制点满足矩阵 C 可逆就可以,但是论文中给出了一个具体的控制点确定方法。3D参考点集为pwi{i=1,⋯,n},选择3D参考点的重心为第一个控制点: 进而得到矩阵: 记ATA(T表示转置)的特征值为λc,i,i=1,2,3,对应的特征向量为vc,i,i=1,2,3 那么剩余的三个控制点可以按照下面的公式来确定:求解控制点在摄像机坐标下的坐标
设K 是摄像头的内参矩阵,可以通过标定获得{ui} i=1....n 是参考点{pi} i=1....n 的2D投影,那么 我们将而且把K 写成焦距fu,fv和光心(uc,vc) 的形式,展开ccj的坐标,的如下式子 从上式可以得到两个线性方程: 把所有n 个点串联起来,我们可以得到一个线性方程组:Mx=0 上式中,vi 是M 的N个零特征值对应的N特征向量。对于第i个控制点:上式中,v[i]k 是特征向量vk 的第i个3×1 sub-vector。我们可以计算MTM 的特征向量得到vi ,但还需要求出{βi} i=1,⋯,N。
这是一个关于{βk} k=1,⋯,N的二次方程,这个方程的特点是没有关于{βk} k=1,⋯,N的一次项。如果将这些二次项βiβj变量替换为βij,那么该方程是{βij } i,j=1,⋯,N的线性方程了。对于4个控制点,可以得到C24 =6个这样的方程。
如果不挖掘任何附加条件,N NN取不同值的时候,新的线性未知数的个数分别为:
- N=1 , 线性未知数的个数为1;
- N=2 ,线性未知数的个数为3;
- N=3 ,线性未知数的个数为6;
- N=4 ,线性未知数的个数为10;
N=4 的时候,未知数的个数多于方程的个数了。注意到βabβcd=βaβbβcβd=βa′b′βc′d′ ,其中{a′,b′,c′,d′}是{a,b,c,d}的一个排列,我们可以减少未知数的个数。举例,如果我们求出了β11,β12,β13,那么我们可以得到β23=β12β13/β11 。这样,即使对于N=4,我们也可以求解出{βij} i,j=1,⋯,N了。
最优化
优化的目标函数就很明确了:一个简单的非线性最优化问题
计算摄像头的位姿
- 计算控制点在摄像头参考坐标下的坐标:
- 计算3D参考点在摄像头参考坐标系下的坐标:
- 计算{pwi} i=1,⋯,n的重心pw0和矩阵A:
- 计算{pci} i=1,⋯,n的重心pc0和矩阵B:
- 计算H:
- 计算位姿中的旋转R:
如果∣R∣<0,那么R(2,:)=−R(2,:)
- 计算位姿中的平移t:
至此,EPNP 算法描述完毕,感谢Jesse 的总结
PNP 问题 P3P解法详解
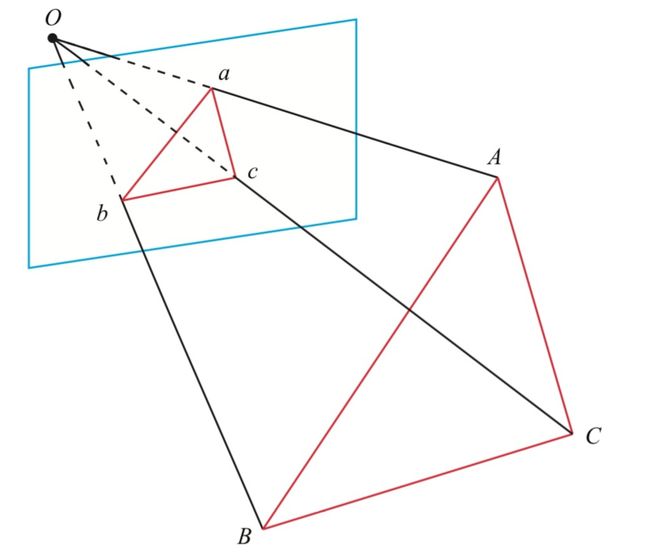
P3P只需要使用3对匹配点。 ABC为三个世界坐标中的点,abc为ABC投影在图像上的点。已知ABC的世界坐标系中的坐标,abc的相机坐标系坐标。O为相机中心,三角形Oac和OAC,Oab和OAB,Obc和OBC两两相似。根据余弦定理有可以看出式子中有3个未知数,所以可以解除对应的3个点的解,然后就变成3D-3D的问题了,使用ICP就可以获得最后的相机的姿态了。
OpenCV中SolvePNP使用效果[代码]
#include
#include
void find_rt(cv::Mat iamge ,cv::Mat matrix ,cv::Mat dist_coeffs ,cv::Mat& rvec_mat,cv::Mat& tvec_mat ){
zz::CalibrationMonocular cm; //封装的一个标定类
std::vector image_points;
cm.find_circle(iamge,image_points,cv::Size(4,11),1); //找到图像中的特征点
std::vector image_points_in3d;
cm.init_cicle_opencv_3dpoints(cv::Size(4,11),image_points_in3d,1,1); // 生成图像中的特征点对应的3D空间中的点,以第一个点为坐标原点
cv::solvePnP(image_points_in3d,image_points,matrix,dist_coeffs,rvec_mat,tvec_mat); //调用opencv的solvePnP求解,默认是迭代法求解
}
int main(int argc, char *argv[])
{
cv::Mat image;
image = cv::imread(argv[1]);
cv::Mat intrinsic = cv::Mat(3,3,CV_64FC1,cv::Scalar::all(0));
cv::Mat distortion = cv::Mat(1,5,CV_64FC1,cv::Scalar::all(0));
intrinsic.at(0,0) = 2469.453065156600600;
intrinsic.at(1,1) = 2470.233140630011300;
intrinsic.at(0,2) = 1991.786856389101300;
intrinsic.at(1,2) = 1500.165893152338400;
intrinsic.at(2,2) = 1;
distortion.at(0,0) = 0.031219512203754 ;
distortion.at(0,1) = -0.063477515747468 ;
distortion.at(0,2) = 0.000016372054794 ;
distortion.at(0,3) = -0.000635253902664 ;
distortion.at(0,4) = 0.000000000000000;
cv::Mat l_rvec_mat,l_tvec_mat;
cv::Mat cover_left_image;
cover_left_image = image.clone();
cv::rectangle(cover_left_image,cv::Point(0,0),cv::Point(2000,3000),cv::Scalar(0,0,255),-1,8,0);
find_rt(cover_left_image,intrinsic,distortion,l_rvec_mat,l_tvec_mat);
std::cout<<"rotate vertor:"< 结果
标定板坐标原点相对于相机坐标系的旋转向量 [0.01777733651588947, 0.01795601519257841, 0.01169115601267934]
标定板坐标原点相对于相机坐标系的旋转向量[0.0213250098434544, -0.06994240284869389, 0.2992679424216718]
和我当时拍摄的效果应该差不多。
重要的事情说三遍:
如果您看到我的文章对您有所帮助,那就点个赞呗 ( * ^ __ ^ * )
如果您看到我的文章对您有所帮助,那就点个赞呗( * ^ __ ^ * )
如果您看到我的文章对您有所帮助,那就点个赞呗( * ^ __ ^ * )
传统2D计算机视觉学习笔记目录传送门
传统3D计算机视觉学习笔记目录传送门
任何人或团体、机构全部转载或者部分转载、摘录,请保留本博客链接或标注来源。博客地址:开飞机的乔巴
作者简介:开飞机的乔巴(WeChat:zhangzheng-thu),现主要从事机器人抓取视觉系统以及三维重建等3D视觉相关方面,另外对slam以及深度学习技术也颇感兴趣,欢迎加我微信或留言交流相关工作。