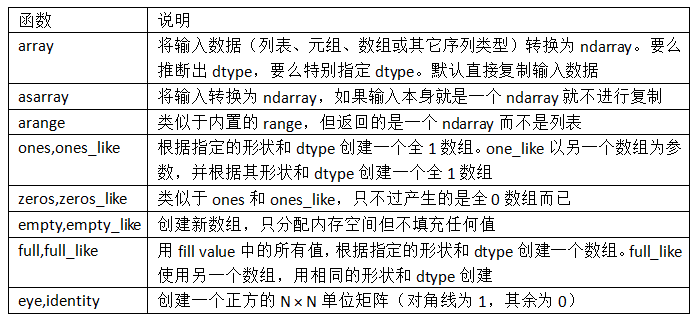
NumPy是Python数值计算最重要的基础包,提供大多数的科学计算方法。其本身并没有多么高级的数据分析功能,但是理解NumPy数组以及面向数学的计算将有助于高效使用Pandas等工具。
NumPy的主要优点如下:
1.ndarry,一个具有矢量运算和复杂广播能力的快速且节省空间的多维数组。
2.可以对整组数据进行快速运算而无需编写循环。
3.具有用于读写磁盘数据的工具,以及用于操作内存映射文件的工具。
4.有线性代数、随机数生成以及傅里叶变换等功能。
5.用于集成由C、C++、Fortran等语言编写的代码的API。
NumPy的ndarray:一种多维数组对象
NumPy最重要的一个特点就是其N维数组对象(即ndarray),该对象是一个快速而灵活的大数据集容器。
In [1]: import numpy as np
In [2]: data = np.random.randn(2, 3)
In [3]: print(data)
[[ 0.08580635 0.92551568 -0.35612221],
[-0.17496393 0.89460353 0.67737304]]
In [4]: print(data*10)
[[ 0.85806352 9.25515676 -3.56122214],
[-1.74963933 8.94603528 6.77373042]]
ndarray的所有元素必须是相同类型的,每个数组都有一个shape(一个表示各维度大小的元组)和dtype(一个用于说明数组数据类型的对象):
In [7]: print(data.shape)
(2, 3)
In [8]: print(data.dtype)
float64
创建ndarray
创建ndarray对象最简单的方法就是使用numpy.array函数
In [24]: data1 = [1, 2, 3, 4]
In [25]: arr1 = np.array(data1)
In [26]: print(arr1)
[1 2 3 4]
In [27]: print(type(arr1))
嵌套序列将会被转换成一个多为数组,可以用ndim属性查看ndarray对象的维数
In [32]: data2 = [ [1, 2, 3, 4], [5, 6, 7, 8] ]
In [33]: arr2 = np.array(data2)
In [34]: print(arr2)
[[1 2 3 4]
[5 6 7 8]]
In [35]: print(arr2.ndim)
2
除numpy.array之外,还有一些函数也可以用来新建数组。比如zeros和ones分别可以创建指定长度或形状的全0或全1数组。empty还可以创建一个没有任何元素的数组,要用这些方法创建多维数组,需要传入一个表示形状的元组即可。还可以用numpy.arange函数生成元素递增的数组,用linspace生成等间隔值的数组。
In [36]: print(np.zeros(10))
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
In [37]: print(np.ones((2,3)))
[[ 1. 1. 1.]
[ 1. 1. 1.]]
In [38]: print(np.arange(10))
[0 1 2 3 4 5 6 7 8 9]
In [39]: np.linspace(2,3,5) # 前两个参数指定起止范围,第三个参数指定产生几个数
Out[39]: array([ 2. , 2.25, 2.5 , 2.75, 3. ]) # 生成与目标数组结构一致的全0数组
In [40]: np.zeros_like(np.arange(12).reshape(2,2,3))
Out[40]:
array([[[0, 0, 0],
[0, 0, 0]],
[[0, 0, 0],
[0, 0, 0]]])
还有一些参照其他对象创建相同结构的函数,如图片中所示:
ndarray的数据类型
dtype是一个特殊的对象,它含有ndarray将一块内存解释为特定数据类型所需的信息,可以在用numpy.array函数初始化对象时作为第二个参数来指定生成对象内部的元素类型。虽然平时用不到,但是当我们在操作大数据集时就需要严格设计和指定存储类型了。
如果想要对一个已经存在的对象做元素类型的调整,则可以借助astype方法。不过需要注意的是如果把浮点数强转成整形数会丢失小数部分。该方法也可以将字符串中的值转化成整形或浮点型数据。
In [46]: numeric_strings = np.array(['1.25', '-9.6', '42'], dtype=np.string_)
In [47]: print(numeric_strings.astype(np.float64))
[ 1.25 -9.6 42. ]
NumPy数组的运算
对nparray对象所做的常规数值运算和逻辑运算都会作用到每一个元素当中
In [48]: arr = np.array([ [1, 2, 3], [4, 5, 6] ])
In [49]: print(arr > 3)
[[False False False]
[ True True True]]
In [50]: print(arr**2)
[[ 1 4 9]
[16 25 36]]
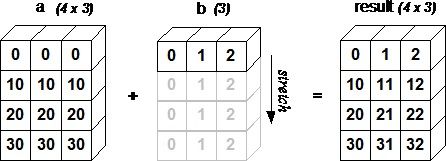
数组的广播
如果两个数组的维数不同,则元素到元素的操作是不可能的。但是在NumPy中仍然可以对形状不相似的数组进行操作,因为它拥有广播功能。广播遵循的规则如下:
1.所有用于计算的输入数组都向其中元素个数最多的那一维看齐,元素个数不足的部分通过在前面补1对齐。
2.输出数组中每一维的长度是输入数组中该维对应的最大长度。
3.如果某个输入数组的某个维和输出数组的对应维长度相同或者其长度为1时,这个数组能够用来计算,否则出错。
4.当输入数组的某个维的长度为1时,沿着此维运算时都用此维上的第一组值。
In [51]: a = np.array([ [0, 0, 0], [10, 10, 10], [20, 20, 20] ])
In [52]: b = np.array([1, 2, 3])
In [53]: print(a.shape)
(3, 3)
In [54]: print(b.shape)
(3,)
In [55]: print(a+b)
[[ 1 2 3]
[11 12 13]
[21 22 23]]
In [56]: print((a+b).shape)
(3, 3)
注意,主动对齐的数组会在缺失维上进行元素复制补齐,达到与输出数组相同的结构。如果与其他维的维数相同但长度不同,则不能完成广播。
In [82]: print(a)
[[ 0 0 0]
[10 10 10]
[20 20 20]]
In [83]: print(d)
[1 2]
In [84]: print(a + d)
---------------------------------------------------------------------------
ValueError
基本的索引和切片
NumPy数组的索引和切片的用法和Python中数组的操作绝大部分一致,不同的地方在于NumPy数组对切片后的子集进行的赋值操作可以利用广播,而且切片的结果是原数组的子集映射。如果想得到ndarray对象切片的副本而不是映射,就要使用数组的copy方法。
In [96]: arr = np.arange(10)
In [97]: arr[5:8] = 11
In [98]: print(arr)
[ 0 1 2 3 4 11 11 11 8 9]
In [99]: arr_slice = arr[5:8]
In [100]: arr_slice[1] = 22
In [101]: print(arr)
[ 0 1 2 3 4 11 22 11 8 9]
In [102]: arr_slice1 = arr[5:8].copy()
In [103]: arr_slice1[1] = 33
In [104]: print(arr)
[ 0 1 2 3 4 11 22 11 8 9]
在索引的使用上,ndarray对多维数组的取值方法做了简化。索引不光可以取元素值,还可以取维度上的数组。同样的也可以使用索引+切片的方式来取低维度的数组。
In [108]: arr = np.array([ [ [1,2], [3, 4] ], [ [5,6], [7, 8] ] ])
In [109]: print(arr)
[[[1 2]
[3 4]]
[[5 6]
[7 8]]]
In [110]: print(arr[0,0])
[1 2]
In [111]: print(arr[0, :1, 0:1])
[[1]]
nparray数组可以像其他单元素对象一样进行逻辑运算,numpy会拿数组中的每一个元素依次进行逻辑运算,并返回一个相同结构但内容用逻辑判断结果(True和False)填充的数组。这个数组同样可以用在数组索引取值当中,会将数组中True元素的位置当做下标来取值。
In [132]: a = np.array([2,3,4,5,6,7,8])
In [133]: a[a>=6]
Out[133]: array([6, 7, 8])
~操作符可以用来反转条件
In [134]: a[~(a>=6)]
Out[134]: array([2, 3, 4, 5])
ndarray数组下标中还可以使用逻辑运算符&(和)、|(或),这里使用Python的and和or关键字无效
In [140]: arr = np.array([1,2,3,4,5])
In [141]: arr1 = np.array([11,22,33,44,55])
In [142]: arr1[(arr == 1) | (arr == 4)]
Out[142]: array([11, 44])
我们可以利用ndarray数组的巧妙的特性来灵活操作数组中的元素,在下标中使用逻辑运算的方法通常会使用到批量修改元素值当中
In [147]: arr
Out[147]: array([1, 2, 3, 4, 5])
In [148]: arr[arr>3] = 0
In [149]: arr
Out[149]: array([1, 2, 3, 0, 0])
花式索引
ndarray数组索引的强大的功能导致了操作数组元素的方式变得十分灵活。我们可以利用下标分隔取值的特性对数组元素排序(负数索引表示从尾部开始取)
In [188]: arr = np.empty((8, 3), dtype='int32')
In [189]: print(arr)
[[0 0 0]
[0 0 0]
[0 0 0]
[0 0 0]
[0 0 0]
[0 0 0]
[0 0 0]
[0 0 0]]
In [190]: for i in range(8):
...: arr[i] = i
...:
In [191]: print(arr)
[[0 0 0]
[1 1 1]
[2 2 2]
[3 3 3]
[4 4 4]
[5 5 5]
[6 6 6]
[7 7 7]]
In [192]: print(arr[[4,3,2,1]])
[[4 4 4]
[3 3 3]
[2 2 2]
[1 1 1]]
In [201]: print(arr[[-1,-2,-3]])
Out[201]:
([[7, 7, 7],
[6, 6, 6],
[5, 5, 5]])
一次传入多个索引数组会有点特别,它返回的是一个一位数组,其中的元素为各个索引元组对应位置取值的结果。其实无论数组是多少维,这种花式索引的结果总是一维的,而且花式索引跟切片不一样,它总是将数据复制到新数组中。
In [202]: arr = np.arange(32).reshape(8,4)
In [203]: print(arr)
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]
[12 13 14 15]
[16 17 18 19]
[20 21 22 23]
[24 25 26 27]
[28 29 30 31]]
In [204]: arr[[1,5,7,2], [0,3,1,2]] # 选取的元素为(1,0)、(5,3)、(7,1)、(2,2)
Out[204]: array([ 4, 23, 29, 10])
数组转置和轴对换
数组的转置是对数学中矩阵转置的实现,是通过adarray数组的.T方法实现的。对于多维数组,T方法转置的结果是之前维度的逆排列(如234格式的数组转置结果是432)。但是transpose方法可以自定义调整维度的顺序,同样的效果还可以使用swapaxes进行轴位置的对换,这两种方法使用的参数都是轴编号,轴按照维度从0开始编号。
In [213]: arr = np.arange(24).reshape(2,3,4)
In [214]: arr.shape
Out[214]: (2, 3, 4)
In [215]: arr.T.shape
Out[215]: (4, 3, 2)
In [216]: arr.transpose((2,0,1)).shape
Out[216]: (4, 2, 3)
In [217]: arr.swapaxes(0,1).shape
Out[217]: (3, 2, 4)
在进行矩阵计算时,常用的方法还有计算矩阵内积的函数dot
In [226]: arr = np.arange(8).reshape(2,4)
In [227]: print(arr.dot(arr.T))
[[ 14 38]
[ 38 126]]
通用函数
通用函数ufunc是一种对ndarray中的数据执行元素级运算的函数。许多ufunc都是简单函数的元素级变体,如sqrt(开平方根)和 exp(求指数):
In [236]: arr = np.arange(10)
In [237]: print(np.exp(arr))
[ 1.00000000e+00 2.71828183e+00 7.38905610e+00 2.00855369e+01
5.45981500e+01 1.48413159e+02 4.03428793e+02 1.09663316e+03
2.98095799e+03 8.10308393e+03]
In [238]: print(np.sqrt(arr))
[ 0. 1. 1.41421356 1.73205081 2. 2.23606798
2.44948974 2.64575131 2.82842712 3. ]
还有一些接收两个数组的ufunc
In [244]: arr = np.random.randn(5)
In [245]: print(arr)
[-0.17874188 0.05965728 -0.59996665 -0.84939912 2.09192082]
In [246]: arr1 = np.random.randn(5)
In [247]: print(arr1)
[ 0.14917549 -1.26410821 1.61575082 0.89258044 -0.92101683]
In [248]: np.maximum(arr, arr1)
Out[248]: array([ 0.14917549, 0.05965728, 1.61575082, 0.89258044, 2.09192082])
In [250]: np.add(arr, arr1)
Out[249]: array([-0.02956639, -1.20445093, 1.01578416, 0.04318131, 1.17090399])
虽然并不常见,但有些ufunc可以返回多个数组,例如modf可以分离浮点数的整数和小数部分并返回存有两种值的数组。
In [252]: remainder, whole_part = np.modf(np.random.randn(5)*10)
In [253]: print(remainder, whole_part)
[ 0.26698189 -0.42003514 0.38117795 -0.48131222 0.95970072]
[ 5. -1. 1. -17. 4.]
利用数组进行数据处理
NumPy数组是你可以将许多种数据处理人物表述为简洁的数组表达式而不用使用循环,这种方法通常被称为矢量化。
假如我们要在一组值上计算函数 √(x2+y2) ,np.meshgrid函数只能接收两个一维数组,并且产生两个二维矩阵,产生方法如下
In [269]: arr = np.arange(-2,2)
In [270]: arr1 = np.arange(0,3)
In [271]: print(arr)
[-2 -1 0 1]
In [272]: print(arr1)
[0 1 2]
In [275]: xs, ys = np.meshgrid(arr, arr1)
In [276]: print(xs)
[[-2 -1 0 1]
[-2 -1 0 1]
[-2 -1 0 1]]
In [277]: print(ys)
[[0 0 0 0]
[1 1 1 1]
[2 2 2 2]]
借助这两个数组就可以很容易的计算 √(x2+y2) 的值了
In [279]: print(np.sqrt(xs**2 + ys**2))
[[ 2. 1. 0. 1. ]
[ 2.23606798 1.41421356 1. 1.41421356]
[ 2.82842712 2.23606798 2. 2.23606798]]
将条件逻辑表述为数组运算
numpy.where函数是三元表达式 x if condition else y 的矢量化版本。假如我们有一个布尔数组和连个值数组,要求根据布尔数组的元素作为条件对两个数值数组依次取值。如果根据Python的写法会对三个数组进行比遍历,而且对于多维数组的处理也颇为麻烦。where函数就可以很好的处理这种情况
In [31]: xarr = np.arange(10)
In [32]: yarr = np.arange(100, 110)
In [33]: cond = np.random.randn(10) > 0
In [34]: print(cond)
[False True False True False False False True True False]
In [35]: result = np.where(cond, xarr, yarr)
In [36]: print(result)
[100 1 102 3 104 105 106 7 8 109]
numpy.where的第二个和第三个参数不必是数组,他们都可以是标量值。在数据分析中,where通常用来根据一个数组而产生一个新的数组。以下是一个将大于0的数替换成1,其余数替换成0的操作
In [37]: arr = np.random.randn(4, 4)
In [38]: print(arr)
[[ 4.17378748e-04 4.53577065e-01 -4.31927376e-01 4.74446118e-01]
[ 3.17704567e-01 1.88555575e-01 -3.62754038e-01 8.39329474e-01]
[ -8.11177153e-01 2.54863827e-01 1.71372714e+00 -5.73967761e-01]
[ 1.03179921e-02 -1.62201948e+00 -1.19052776e+00 -8.33251994e-01]]
In [39]: print(np.where(arr>0, 1, 0))
[[1 1 0 1]
[1 1 0 1]
[0 1 1 0]
[1 0 0 0]]
数学和统计方法
在进行数学和统计方面的运算时,可以通过数组的一些数学函数对整个数组或某个轴向的数据进行统计计算。sum、mean以及标准差std等聚合计算即可以当做数组的实例方法调用,也可以当做顶级NumPy函数使用。mean(平均值函数)和sum(求和函数)这类函数可以接收一个axis选项参数,用于计算该轴向上的统计值,最终结果是一个少一维的数组
In [65]: arr = np.arange(24).reshape(2,3,4)
In [66]: print(arr)
[[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
[[12 13 14 15]
[16 17 18 19]
[20 21 22 23]]]
In [67]: print(arr.mean())
11.5
In [68]: print(arr.mean(axis=1))
[[ 4. 5. 6. 7.]
[ 16. 17. 18. 19.]]
In [69]: print(arr.sum(axis=1))
[[12 15 18 21]
[48 51 54 57]]
其他如comsum(累加)和cumprod(累乘)之类的方法产生的是一个由中间结果组成的数组
In [70]: arr = np.arange(10)
In [71]: print(arr.cumsum())
[ 0 1 3 6 10 15 21 28 36 45]
In [72]: arr = np.arange(12).reshape(3,4)
In [73]: print(arr.cumsum(axis=1))
[[ 0 1 3 6]
[ 4 9 15 22]
[ 8 17 27 38]]
上面这些方法中,布尔值会被强制转换成1和0。另外还有两个函数all(是否全为True值)和any(是否存在True值)对处理布尔数组很实用。
In [75]: bools = np.where(np.random.randn(10)>0, 1, 0)
In [76]: print(bools.any())
True
In [77]: print(bools.all())
False
另外还有求上三角矩阵元素坐标的函数 triu_indices_from等(持续补充)
In [38]: data = np.random.rand(4,4)
In [39]: np.triu_indices_from(np.zeros_like(data))
Out[39]:
(array([0, 0, 0, 0, 1, 1, 1, 2, 2, 3], dtype=int64),
array([0, 1, 2, 3, 1, 2, 3, 2, 3, 3], dtype=int64))
In [40]: data[np.triu_indices_from(np.zeros_like(data))] = 0
In [41]: data
Out[41]:
array([[ 0. , 0. , 0. , 0. ],
[ 0.35160052, 0. , 0. , 0. ],
[ 0.70959398, 0.29337074, 0. , 0. ],
[ 0.6316058 , 0.77302342, 0.23235628, 0. ]])
排序
NumPy中提供了各种排序相关功能,这些排序函数实现不同的排序算法,每个排序算法的特征在于执行速度、最坏情况性能、所需工作控件和算法的稳定性。下标为三种排序算法的比较
numpy.sort(a, axis, kind, order)函数返回输入数组的排序副本,它的参数kind可以指定上面三种排序方式(默认是'quicksort'),order如果包含数组字段,则是要排序的字段。
In [94]: a = np.random.randint(-15, 15, 24).reshape(2,3,4)
In [95]: print(a)
[[[ 2 2 2 13]
[ 12 7 14 -12]
[ 6 -1 4 -11]]
[[ 8 11 -13 -5]
[ 4 -13 12 -5]
[-10 -7 0 12]]]
In [96]: print(np.sort(a, axis=1))
[[[ 2 -1 2 -12]
[ 6 2 4 -11]
[ 12 7 14 13]]
[[-10 -13 -13 -5]
[ 4 -7 0 -5]
[ 8 11 12 12]]]
In [97]: dt = np.dtype([('name', 'S10'),('age', int)]) # ‘S10’为固定用法
In [98]: a = np.array([("raju",21),("anil",25),("ravi", 17), ("amar",27)], dtype = dt)
In [99]: print(a)
[(b'raju', 21) (b'anil', 25) (b'ravi', 17) (b'amar', 27)]
numpy.argsort函数对输入数组沿给定轴执行间接排序,并使用指定排序类型返回数据排序后的索引顺序。
In [103]: arr = np.array([3,1,2])
In [104]: print(arr.argsort())
[1 2 0]
In [105]: print(arr)
[3 1 2]
与numpy.argsort类似,numpy.lexsort函数可以利用后一个数组的键来对前一个数组进行排序。
In [113]: a=[1,5,1,4,3,4,4]
In [114]: b=[9,4,0,4,0,2,1]
In [115]: print(np.lexsort((a,b)))
[2 4 6 5 3 1 0]
In [116]: print(np.lexsort((b, a)))
[2 0 4 6 5 3 1]
唯一化以及其它的集合逻辑
NumPy提供了一些针对一维ndarray的集合基本运算,比较常用的unique函数可以对一位数组进行值去重,并对结果进行排序
In [122]: names = np.array(['Bob', 'Will', 'Joe', 'Bob', 'Will', 'Joe', 'Joe'])
In [123]: print(np.unique(names))
['Bob' 'Joe' 'Will']
另一个函数numpy.in1d用于测试一个数组元素在另一个数组中的存在情况
In [124]: values = np.array([6, 0, 0, 3, 2, 5, 6])
In [125]: print(np.in1d(values, [2, 3, 6]))
[ True False False True True False True]
用于数组的文件IO
numpy.save和numpy.load是读写磁盘数组数据的两个主要函数。默认情况下,数组是以未压缩的原始二进制格式保存在扩展名为 .npy 的文件中,如果文件路径末尾没有扩展名 .npy 则在创建时会自动加上
In [129]: arr = np.arange(10)
In [130]: np.save('E:\some_array', arr)
In [131]: file_array = np.load('E:\some_array.npz')
In [132]: print(file_array)
[0 1 2 3 4 5 6 7 8 9]
numpy.savez可以同时保存多项数据,保存的时候要给数据指定键名,取数据时需要用键名取。想压缩数据还可以使用numpy.savez_compressed代替numpy.savez。
In [160]: np.savez('E:\some_array.npz', a=arr, b=[4,3,2,1])
In [161]: file_array = np.load('E:\some_array.npz')
In [162]: file_array.files
Out[162]: ['a', 'b']
In [163]: print(file_array['b'])
[4 3 2 1]
线性代数
@符号可以进行矩阵的乘法运算,类似于numpy.dot函数,不过其职能用于操作ndarray对象
In [165]: a = np.array([[1,2,3], [4,5,6]])
In [166]: b = np.array([[1,1,1,1],[2,2,2,2],[3,3,3,3]])
In [167]: print(a @ b)
[[14 14 14 14]
[32 32 32 32]]
此外,numpy.linalg中有一组标准的矩阵分解运算以及诸如求逆和行列式之类的东西。它们跟MATLAB使用的是相同的行业标准线性代数库。
伪随机数生成
numpy.random模块对Python内置的random进行了补充,增加了一些用于高效生成多种概率分布的样本值的函数。例如可以使用normal函数生成标准的正态分布数组
In [177]: samples = np.random.normal(size=(4,4))
In [178]: print(samples)
[[-1.62410575 -0.29267354 0.54842487 0.53761778]
[-0.61073399 -0.57042705 0.30861203 2.02920307]
[-1.18348343 -1.99581203 -2.21354806 0.68337904]
[-0.14544606 -0.31720171 1.69943308 -0.30445943]]
而Python内置的random模块只能一次生成一个样本值,面对大量的随机数需求场景时numpy.random比Python的生成速度快非常多。我们说这些都是伪随机数是因为它们都是通过算法基于随机数生成器种子,在确定性的条件下生成的,你可以使用NumPy的np.random.seed更改随机数生成种子。numpy.random的数据生成函数使用了全局的随机种子,要避免全局状态可以使用numpy.random.RandomState创建一个与其他隔离的随机数生成器。
In [179]: np.random.seed(1234)
In [180]: rng = np.random.RandomState(1234)
In [181]: print(rng.randn(10))
[ 0.47143516 -1.19097569 1.43270697 -0.3126519 -0.72058873 0.88716294
0.85958841 -0.6365235 0.01569637 -2.24268495]