前言
我们都见识了不少关于递归与尾递归的各种长篇概论,本文将通过对下面几个问题的直观体验,来帮助加深对递归的理解。
本文内容目录:
- 什么是调用栈?
- 什么是递归函数?
- 递归的调用栈是怎样?
- 尾递归的调用栈是怎样?
- 为什么说尾递归的实现在本质上是跟循环等价?
-
什么是调用栈?
栈 是一种常见的数据结构,具有后进先出(LIFO)的特点。
调用栈 则是计算机内部对函数调用所分配内存时的一种栈结构。
-
什么是递归函数?
递归函数 简单的讲,就是函数在内部调用自己。
在编写递归函数的时候,我们要注意组成它的两个条件,分别是:基线条件 和 递归条件 (也叫回归条件)。
递归函数其实是利用了分而治之的思想(Divide and Conquer D&C),下面用一个简单的递归函数来说明。
假设我们现在需要一个递增函数increasing(n),其实现为:
def increasing(n = 0):
print('n = %d' % n)
increasing(n + 1)
我们很容易发现,这样的代码会永不休止的执行,最后会造成栈溢出,简单的说就是内存满了。因为根本没人告诉它什么时候该停下来,所以它不断的重复执行,造成无限循环。
假设递增的值到100的时候就不再执行,则其实现为:
def increasing(n = 0):
print('n = %d' % n)
if n == 100: // --> 基线条件
return
else: // --> 递归条件
increasing(n + 1)
从上面可以看出,递归条件指的是函数在内部继续调用自己,基线条件指的是函数不再调用自己的情况。
所谓 Divide and Conquer,分别对应的则是递归条件和基线条件。
-
递归的调用栈是怎样?
下面我们通过计算一个数的阶乘的函数进行解释。它将会有三个不同版本,分别是递归求阶乘,尾递归求阶乘,for循环求阶乘。
因为这里要研究递归的调用栈情况,所以我们先来看看递归求阶乘的实现:
print('##### 递归求阶乘 #####')
def fact(n):
if n == 1:
return 1
else:
return n * fact(n - 1)
print('result = %s' % fact(4))
为了更好的解释说明,我将上面的代码略作改动:
print('##### 递归求阶乘 #####')
def fact(n):
if n == 1:
result = 1
return result
else:
print('current: n = %d, result = %d * fact(%d - 1)' % (n, n, n))
result = fact(n - 1)
return n * result
改动理由:
- 调用栈中的函数都保留计算结果变量 result,要特别注意的是调用栈中的各个函数内部的变量对函数彼此而言是互相隔离无法访问的。
- 在递归条件中打印活跃期的情况。
所谓活跃期,指的是计算机当前所操作的函数执行期。
运行结果为:
##### 递归求阶乘 #####
current: n = 4, result = 4 * fact(4 - 1)
current: n = 3, result = 3 * fact(3 - 1)
current: n = 2, result = 2 * fact(2 - 1)
result = 24
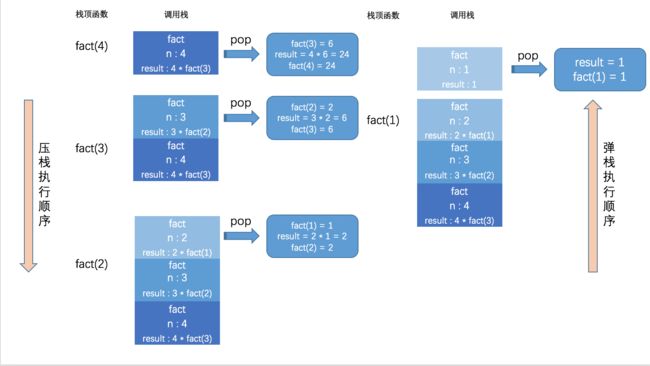
其调用栈情况:
正常情况下,栈顶函数执行完毕后将弹出。但我们却看到递归函数的调用不断的向调用栈压入执行函数,那么问题来了,为什么调用栈前面的函数"执行完毕"后不自动弹出呢?
答案是 栈顶函数其实并未执行完成,因为栈顶函数的变量result的值尚未确定,它还需要 下一个递归函数返回的值(上下文) 来计算,所以一直处于非活跃期状态被保留在调用栈中。
上面的答案还需完善一下,因为当某个栈顶函数,例如fact(1),在执行到基线条件时,result的值已经确定下来,而无需等待下一个递归函数的上下文,所以该栈顶函数真正执行完毕,并弹出调用栈。又因为下一个栈顶函数可以拿到已弹栈的函数返回的上下文,因而当弹栈函数交待完成后,也相继弹出调用栈。
-
尾递归的调用栈是怎样?
我们先来看看尾递归求阶乘的实现:
print('##### 尾递归求阶乘 #####')
def fact_tail(n):
return tail_fact_count(n)
def tail_fact_count(n, result = 1):
if n == 1:
return result
else:
print('current: n = %d, result = %d' % (n, result))
print('next: n = %d, result = %d' % (n - 1, result * n))
print('----------------')
return tail_fact_count(n - 1, n * result)
print('result = %s' % fact_tail(4))
同样的,我们将上述代码略作改动:
print('##### 尾递归求阶乘 #####')
def fact_tail(n):
result = tail_fact_count(n)
return result
def tail_fact_count(n, result = 1):
if n == 1:
return result
else:
print('current: n = %d, result = %d' % (n, result))
print('next: n = %d, result = %d' % (n - 1, result * n))
print('----------------')
result = n * result
n = n - 1
return tail_fact_count(n, result)
print('result = %s' % fact_tail(4))
运行结果为:
##### 尾递归求阶乘 #####
current: n = 4, result = 1
next: n = 3, result = 4
----------------
current: n = 3, result = 4
next: n = 2, result = 12
----------------
current: n = 2, result = 12
next: n = 1, result = 24
----------------
result = 24
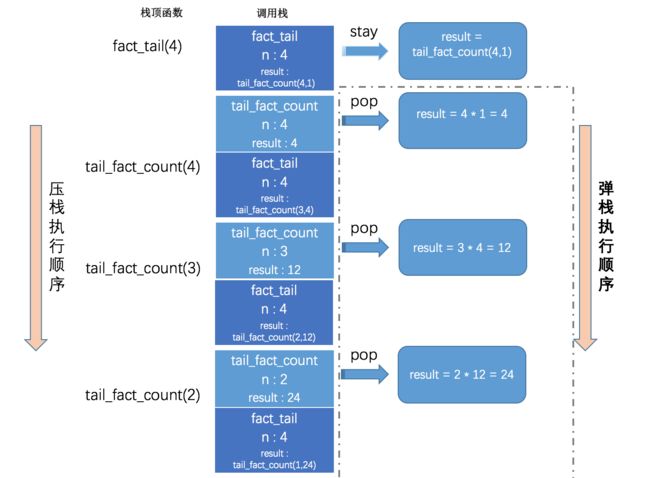
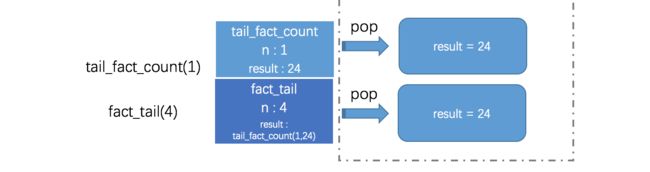
我们再来看看它的调用栈情况:
仔细对比前面递归函数的调用栈情况,我们可以看出递归与尾递归调用栈的两个明显不同点:
- 尾递归的调用栈明显比递归的调用栈清爽很多。
- 尾递归弹栈顺序是由上至下执行;而递归弹栈顺序是由下至上执行的。(这里的弹栈顺序指的不是物理顺序)
我们再来看看前面递归函数的实现。在递归实现中,result的值因为需要 下一个递归函数返回的值 来计算才能确定,所以栈顶函数(设A)一直在调用栈中停留等待下一个栈顶函数(设B)的返回值,一旦下一个栈顶函数(B)返回了确切的result值,那么当B交待完成之后就会弹出,所谓交待即是因为上一个栈顶函数A需要下一个栈顶函数即B的返回值,当A拿到了B的值就是交待完成了。以此类推,递归的弹栈顺序则如图所示由下往上弹出。
那么尾递归究竟做了什么猫腻?
尾递归其实在result的值上做了猫腻。在尾递归的实现中,result的值在当前栈顶函数中已经确定下来了,并经计算后交待给下一个栈顶函数。所以当栈顶函数完成了它的使命(把result值传递给下一个执行函数),它就会愉快的在调用栈上弹出。
归纳来讲:
- 递归函数需要将整个函数作为上下文来完成 目的。
- 尾递归则把 目的 在当前函数中完成,并交待给下一个函数。
在本例子中的 目的 指的是确定result值。
-
为什么说尾递归的实现在本质上是跟循环等价?
按照惯例,先上代码。但是为了更好的理解与尾递归的联系,最好还是花个十几秒思考一下如何实现for循环求阶乘吧~
为了减少篇幅,直接贴上略作修改的代码:
print('##### for循环求阶乘 #####')
def fact_for(n):
if n == 1:
return 1
else:
result = 1
for i in range(n, 0, -1):
print('current: n = %d, result = %d' % (i, result))
result = for_fact_count(i, result)
return result
def for_fact_count(n, result = 1):
return n * result
print('result = %s' % fact_for(4))
运行结果为:
##### for循环求阶乘 #####
current: n = 4, result = 1
current: n = 3, result = 4
current: n = 2, result = 12
current: n = 1, result = 24
result = 24
当我们思考如何使用for循环去实现求阶乘的过程中,我们会想到用一个变量去存储计算的值。在上述代码中指的就是 result (= 1)。
为了便于理解for循环与尾递归,我设计了这么一个函数 for_fact_count(n, result = 1),它接收 当前result值并经计算后刷新result值。
在不影响for循环的实现我已经将其与尾递归的实现做了相似的转化(连名字的都好相似啦),所以请开始你的表演,把for循环求阶乘的调用栈画出来吧~
结语:
- 虽说本文使用了Python进行编码解释,但是目前大多数编程语言都没有针对尾递归做优化,Python解释器也没有,所以即便使用了尾递归进行求阶乘,在运行过程中还是会造成栈溢出。而Xcode在debug环境下不会对尾递归做优化,需将其设为release。
- 小生才疏浅陋,文中难免有错漏之处,请多多指教,感谢您的阅读。