预测分析 第二章（中）

2.4　评估线性回归模型

再次利用lm()函数，用线性回归模型来拟合数据。我们的两套数据集会用到上述数据框里剩下的所有输入特征。R提供了一种编写公式的简写方式，它可以把某个数据框里的所有列作为特征，除了被选为输出的列之外。这是利用一个句号符来完成的，如下列代码片段所示：

machine_model1 <- lm(PRP ~ ., data = machine_train)
cars_model1 <- lm(Price ~ ., data = cars_train)

训练集浏览

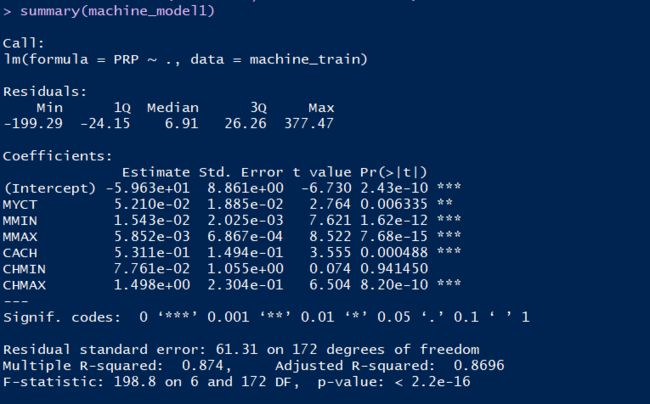
一旦我们准备好了所有的数据，训练一个线性回归模型就是一行代码的事情，但是如果要研究这个模型以便判定其效果，后面就会有重要的工作。幸运的是，我们可以利用summary()函数立刻获得某些关于这个模型的重要信息。该函数对于CPU数据集的输出如下所示：

summary(machine_model1)

machine训练集回归模型信息

在重复了一次之前对lm()函数本身的调用之后，summary()函数给出的信息形成了三个独立的部分。第一部分是模型残差（residual）的摘要，它是模型对训练它的数据中的观测数据产生的误差。第二部分是一个表格，包含了模型各系数的预测值及其显著性检验的结果。最后几行则显示了该模型的一些总体性能衡量指标。如果在二手车数据集上重复同样的过程，我们会在该模型的摘要里注意到如下的一行：
Coefficients: (1 not defined because of singularities)

cars数据训练集的线性回归模型信息

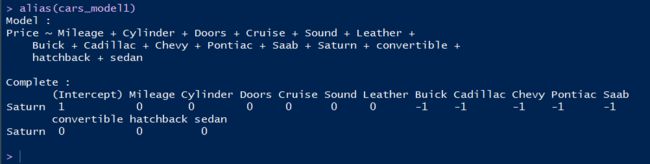
产生这个结果的原因是由于潜在的依赖关系，导致我们还有1个特征对输出的作用无法和其他特征分清楚。这种现象被称为 混叠（aliasing）。alias()命令会显示我们需要从模型中去除的特征：

alias(cars_model1)

显示去除 Saturn特征

正如我们所见，有问题的特征就是Saturn特征，所以我们会去除这个特征并重新训练模型。要从一个线性回归模型去除某个特征，可以把它加到公式中的句点之后，并在它之前加上一个减号：

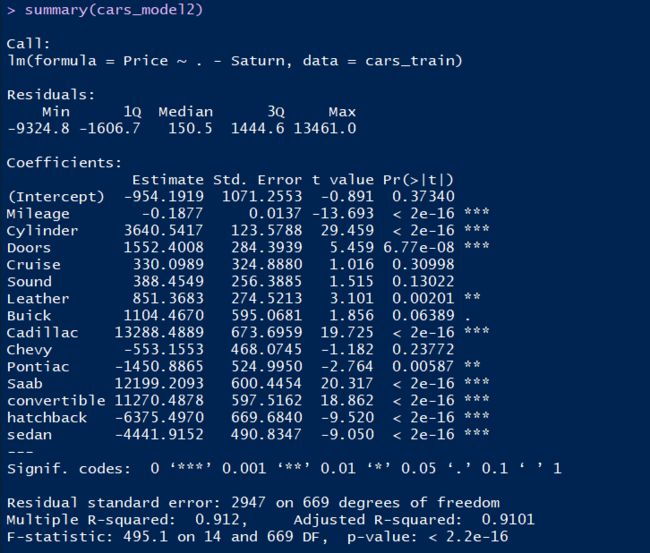
cars_model2 <- lm(Price ~ . - Saturn, data = cars_train)
summary(cars_model2)

cars训练集修正后的回归模型

2.4.1　残差分析

残差就是模型对特定观测数据产生的误差。换言之，它是输出的实际值和预测值之间的差异：

原著中此处公式有误， 为。这里已进行改正，

在构建一个良好的回归模型时，对残差的分析是非常重要的，因为它能体现这个模型的很多方面，从不能成立的假设和拟合的质量到其他问题（比如离群值）。要理解残差摘要里的衡量指标，可以想象把残差从小到大排序。除了在这个序列里两个极端位置上的最小值和最大值之外，这个摘要还会显示第一个和第三个四分位数（quartile），它们分别是这个序列中处于四分之一和四分之三位置的值。中位数（median）则是序列正中位置的值。四分位间距（interquartile range）是序列处于第一和第三个四分位数之间的部分，根据定义可知，它包含了一半数据。首先来看一下CPU模型里的残差摘要，其中有趣的一点是，第一个和第三个四分位数的值与最小和最大值相比是很小的。这是存在一些具有很大残差误差的点的首要迹象。在理想情况下，残差应该具有0中位数和较小的四分位数值。可以通过关注lm()函数所产生模型具有的residuals属性，来重现summary()函数产生的残差摘要：

summary(cars_model2$residuals)
mean(cars_train$Price)

残差分析

注意，在前面关于二手车模型的示例中，我们需要把残差的值和输出变量的平均值进行比较，以获得残差是否过大的印象。这样，前面的结果显示在训练数据中二手车的平均售价为$21k，预测结果的 50% 基本是在正确值的±$1.6k范围内，这个情况看起来是相当合理的。显然，CPU模型的残差的绝对值都小得多，这是因为该模型的输出变量（即发布的CPU相对性能）比二手车模型里的Price变量值要小得多。

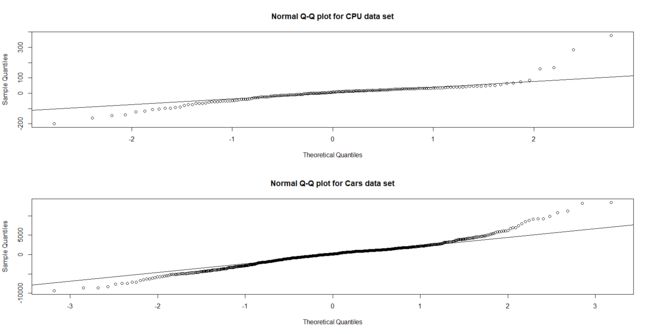
在线性回归里，我们假设模型里不能化简的误差是以正态分布的形式随机分布的。一种称为分位图（Quantile-Quantile plot，Q-Q plot）的诊断图有助于从视觉上评判该假设的符合程度。这种图背后的关键思想是，我们可以通过比较它们分位数（quantile）的值来比较两种分布。一个分布的分位数基本上是一个随机变量的距离均等的区间，这样的每个区间具有相同的概率。例如，四分位数把一个分布划分为4个概率相等的部分。如果两个分布相同，那么分位图就应该是直线y＝x的图形。要检查残差是否符合正态分布，可以用它们的分布和一个正态分布进行比较，查看得到的图形和y＝x的接近程度。

有很多其他的方法可以检查模型残差是否是正态分布。有一个很好的工具是R语言的nortest包，它实现了很多知名的正态性检验方法，包括Anderson-Darling检验和Lilliefors检验。此外，stats包包含了shapiro.test()函数，可以用于进行Shapiro-Wilk正态性检验。

下列代码会对两个数据集创建分位图：

par(mfrow = c(2, 1))
machine_residuals <- machine_model1$residuals
qqnorm(machine_residuals, main = 'Normal Q-Q plot for CPU data set')
qqline(machine_residuals)
cars_residuals <- cars_model2$residuals
qqnorm(cars_residuals, main = 'Normal Q-Q plot for Cars data set')
qqline(cars_residuals)

两个数据集的分位图如下所示：

理论分位图

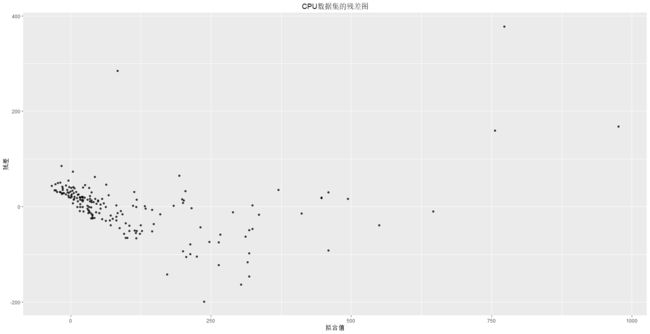
两个模型的残差看起来和理论上的正态分布分位数相当贴近，虽然拟合程度并非完美，但是这对于大部分实际环境数据来说是典型的情况。第二种对线性回归非常有用的诊断图被称为 残差图（residual plot）。它是反映训练数据中观测数据的残差和对应拟合值之间关系的一种图表。换言之，它是配对

的一个图。残差图有两个重要属性是我们特别感兴趣的。首先，我们希望通过检查残差是否在不同的拟合值范围中保持大小一致，来确认有关常数方差的假设是成立的。其次，我们必须检验在残差中不存在某种模式。但是，如果我们观察到了某种模式，它就有可能是一个迹象，表明对应的模型对于涉及的特征是非线性的，或者在模型里有缺失的特征没有被纳入。实际上，一种发现新特征的有用方法就是寻找和模型残差相关的新特征。

CPU数据集的残差图

cars数据集的残差图

mcplt <- data.frame(fitVal = machine_model1$fitted.values, Res = machine_model1$residuals)
carplt <- data.frame(fitVal = cars_model2$fitted.values, Res = cars_model2$residuals)
ggplot(mcplt, aes(x = fitVal, y = Res))+
  geom_point(shape = 19, alpha = 0.7)+
  labs(x = '拟合值', y = '残差')+
  ggtitle('CPU数据集的残差图')+
  theme(plot.title = element_text(hjust = 0.5))

ggplot(carplt, aes(x = fitVal, y = Res))+
  geom_point(shape = 19, alpha = 0.7)+
  labs(x = '拟合值', y = '残差')+
  ggtitle('cars数据集的残差图')+
  theme(plot.title = element_text(hjust = 0.5))

remove(mcplt, carplt)

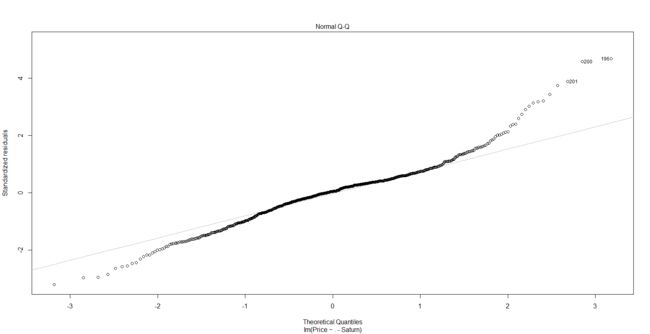
这两张图在图的左侧部分都显示了细微的残差递减模式。稍微更令人担心的是，对于两个输出变量的较大值，残差的方差（the variance of the residual）看起来有点大，这有可能表明误差并不是同方差的（homoscedastic）。这个问题在第二个有关二手车信息的图中更为显著。在前面的两个残差图中，我们也标记了某些较大的残差（绝对值大小）。我们很快还会看到可能有一些潜在的离群值。另一种获得残差图的方法是对lm()函数本身产生的模型调用plot()函数。这样会创建4个诊断图，包括残差图和分位图。

image.png	image.png
image.png	image.png

2.4.2　线性回归的显著性检验

在检查了残差的摘要之后，我们应该关注的下一个东西是模型所产生的系数表。在这里，每个估算出来的系数都配套了额外的一组数值，在最后还有一组星号或点。首先，这样一连串的数值看起来可能有点混乱，但是把所有这些信息包括进来是有充分理由的。当对某些数据收集测量值并指定一组特征来构建一个线性回归模型时经常会遇到的情况是，里面有一个或多个特征和我们要预测的输出实际上并不相关。当然，这是我们在之前收集数据的时候并没有在意的问题。理想情况下，我们会希望这个模型不但找到和输出变量确实存在依赖关系的那些特征所对应的最佳系数值，而且能告诉我们哪些特征是不需要的。

判定模型是否需要某个特征的一种可参考的方法是训练两个模型而不是一个。第二个模型会包含第一个模型的所有特征，再去掉需要确认其显著性的那个特征。然后就可以通过它们残差的分布情况来检验两个模型是否有差别。实际上这就是R语言会对我们在每个模型里指定的所有特征进行的处理。对于每个系数，都会针对它对应的特征和输出变量无关的无效假设（null hypothesis）构建一个置信区间（confidence interval）。具体而言，对于每个系数，我们都会考虑一个包括除了该系数对应的特征之外的所有其他特征的线性模型。然后，我们会检验把这个特征加入模型是否能显著改变残差误差的分布，这种改变会是该特征和输出存在线性关系的证据，如果成立，则该系数就应该是一个非0值。R语言的lm()函数会自动为我们进行这些检验。

在统计学里，置信区间会把一个点估计（point estimate）和该估计的精度合并在一起。具体做法是指定一个区间，在某种程度的可信度下，可以期望要估计的参数的实际值会处于该区间内。某个参数的95%置信区间实际上告诉我们的是，如果要从同一个实验收集 100 个数据样本，并在每个样本里为这个估计的参数构建一个95%的置信区间，那么这些数据样本里有 95 个会满足目标参数的实际值，处于它所对应的置信区间内。对于同样程度的可信度，为方差较大的点估计（例如对只有很少的数据点作出估计的情况）构建的置信区间，和对较小方差作出的估计相比，往往会定义出范围更大的区间。

我们来看看CPU模型的摘要输出的一个快照，它显示了CPU模型中截距和 MYCT 特征的系数：

image.png

我们目前关注的是MYCT特征，它所在行里的第一个数值是其系数的估算值，这个值大约是0.05 (5.210 x 10^(-2))。标准误（standard error）是这个估算值的标准差（standard deviation），它等于下一个数值给出的0.01885。我们可以通过对在0和该系数估算值之间的标准误个数进行计数，判定该系数是否实际为0（代表该特征与输出线性无关）的置信度。为此，我们可以用系数估算值除以标准误，这就是t值（t-value）的定义，也就是该行里的第三个值：

q <- 5.210e-02 / 1.885e-02
> q
[1] 2.763926

这样，我们的MYCT系数值和0值之间几乎隔开了3个标准误的数值，这个指标很好地表明该系数不太可能为0。t值越大，就越能说明我们应该给模型中的这个特征赋予非0的系数值。我们可以把这个绝对数值转变为一个概率，它可以告诉我们该系数的真实值为0的可能性。这个概率是从学生t分布（Student抯 t-distribution）得到的，被称为p值（p-value）。对于MYCT特征，这个概率是0.006335，是很小的。可以利用pt()函数得到这个值：

pt(q, df = 172, lower.tail = F) * 2
> pt(q, df = 172, lower.tail = F) * 2
[1] 0.006333496

pt()函数是t分布的分布函数，而t分布是对称的。为了理解p值以上面这种方式进行计算的原因，要注意我们感兴趣的是t值的绝对值比我们计算的值更大的概率。要得到这个结果，我们首先要获得该t分布上尾或右尾（the upper / right tail）部分的概率，然后将其乘以2，这样就把下尾（the lower tail）部分也包含进来了。运用基本的分布函数在R语言里是一项非常重要的技能，如果前面这个示例看起来难度太大，我们在关于R语言的在线教程里还有一些示例可供参考。t分布是以自由度作为参数的。

自由度的数量实际上是在计算某个统计量（例如某个系数的估计值）时能够自由变化的变量数。在线性回归主题下，它就相当于训练数据中观测数据的个数减去模型中参数的个数（即回归系数的个数）。对于我们的CPU模型，这个数字就是179－7＝172。对于具有更多数据点的二手车模型，这个数字是664。自由度这个名字来源于它和独立维度（或者说，作为某个系统的输入的信息片段）的数量之间的关系，从而反映系统能够（在不违反任何对于输入的约束条件的条件下）自由配置的程度。

作为一般的经验规则，我们会希望p值小于0.05，这相当于我们希望系数不为0值的估计具有95%的置信区间。每个系数旁边的星号数量给我们提供了一种关于置信度水平的快速视觉辅助，其中一颗星对应95%的经验规则，而两颗星代表了99%的置信区间。因此，在模型摘要里，每个不带任何星号的系数对应的就是一个按照经验规则我们没有把握将其纳入模型的特征。在CPU模型里，CHMIN特征是唯一可疑的特征，而其他特征的p值都非常小。二手车模型的情况就不同了。这里，有4个特征都是可疑的，截距也是如此。

在线性回归模型主题下正确理解p值的含义是很重要的。首先，我们不能也不应该对p值进行互相比较来评判哪个特征是最重要的。其次，较高的p值并不一定代表某个特征和输出之间不存在线性关系；它只表明在所有其他模型特征存在时，这个特征对于输出变量不能提供任何新的信息。最后，我们必须永远记住，95%的经验规则并非绝对真理，它只是在特征（以及对应的系数）的数量不是特别大的时候确实有用。在95%的置信度下，如果在模型里有1000个特征，可以预期得到错误系数的结果是50个。因此，线性回归系数的显著性检验对于高维问题并不是那么有用。

最后一个显著性检验值实际上出现在lm()输出摘要的最下部，并且是在最后一行。这一行给我们提供了F统计量（F statistic），其命名来源于检查两个（理想状况下是正态的）分布的方差之间是否存在统计显著性（statistical significance）的F检验（F test）。这个示例中的F统计量尝试评价某个所有系数都为0的模型中的残差方差（the variance of the residuals）是否和我们训练的模型的残差方差有显著性的差异。

换言之，F检验会告诉我们训练的模型是否能解释输出中的某些方差，如果能，我们就知道至少有一个系数必须为非0值。虽然这个检验对于我们有很多系数的情况不是那么有用，但它还是能检验系数的整体显著性，而不会遇到t检验对于单个系数的那种问题。摘要部分对此显示了一个非常小的p值，所以我们知道我们的系数里至少有一个是非0值。我们可以调用anova()函数重现运行过的F检验，该函数代表方差分析（analysis of variance）。该检验会用只有截距而没有特征的方式建立的空模型（null model）和训练模型进行比较。我们要用CPU数据集对这个函数进行如下演示：

machine_model_null <- lm(PRP ~ 1, data = machine_train)
anova(machine_model_null, machine_model1)

image.png

注意，空模型的公式是PRP～1，其中的1代表截距。

2.4.3　线性回归的性能衡量指标

在摘要里，最后的细节是和该模型作为一个整体的性能以及该线性模型和数据的拟合程度相关的。要理解我们如何评估线性回归的拟合，必须首先指出的是，线性回归模型的训练准则是使均方差（MSE）在训练数据上最小化。换言之，把一个线性模型拟合到一组数据点相当于找到一条直线，它的斜率和位置要让它与这些点的距离的平方的总和（或平均值）最小。因为我们把某个数据点和它在该直线上的预测值之间的误差称为残差，我们可以定义残差平方和（Residual Sum of Square，RSS）为所有残差的平方之和：

换言之，RSS就是误差平方和（Sum of Squared Error，SSE），因此我们可以通过下面的简单公式把它和我们已经熟悉的均方差（MSE）联系起来：

除了某些历史原因之外，RSS之所以成为值得注意的重要衡量指标，是因为它和另一个被称为RSE的重要衡量指标相关，我们后续会讨论到RSE。为此，我们需要先对训练线性回归模型的过程有个直观的了解。如果用人工数据多次进行简单线性回归实验，每次改变随机种子（random seed）以获得不同的随机样本，就会得到一组很可能非常接近实际总体回归线的回归线，正如进行单次实验所看到的那样。这表明了一个事实，即线性模型总体而言是具有低方差的特点的。当然，尝试近似的未知函数也有可能是非线性的，如果是这样，那么即使总体回归线也不太可能对于非线性函数的数据产生良好的拟合。这是因为线性假设是非常严格的，因此，线性回归是一种带有较高偏误的方法。

我们要定义一个叫作残差标准差（Residual Standard Error，RSE）的衡量指标，它会估计我们的模型和目标函数之间的标准差。这就是说，它会大致地衡量模型和总体回归线之间的平均距离。它是以输出变量的单位衡量的，并且是一个绝对值。因此，它需要和y的值进行比较，以便判定它对于特定样本是高还是低。带有k个输入特征的模型的一般RSE可以按如下公式计算：

对于简单线性回归，其特征数k＝1：

可以利用前面的公式对两个模型计算RSE值，结果如下所示：

n_machine <- nrow(machine_train)
k_machine <- length(machine_model1$coefficients) - 1
sqrt(sum(machine_model1$residuals ^ 2 / (n_machine - k_machine - 1)))
n_cars <- nrow(cars_train)
k_cars <- length(cars_model2$coefficients) - 1
sqrt(sum(cars_model2$residuals ^ 2 / (n_cars - k_cars - 1)))

image.png

要解释这两个模型的RSE值，就需要把它们和输出变量的均值进行比较：

image.png

注意，在CPU模型中，其取值为61.3的RSE值和二手车模型大约为2947的RSE值相比是相当小的。但是，就它们和对应输出变量的均值的近似程度而言，我们可以看到反而是二手车模型的RSE表现了更优的拟合。

现在，虽然RSE作为一个绝对数值在和输出变量的均值进行比较方面是有用的，但是我们经常需要一个相对数值用来在不同的训练场景下进行比较。为此，在评估线性回归模型的拟合情况时，我们也经常观察统计量（ statistic）。在摘要信息里，它是用“multiple R-squared”来指示的。在提供它的计算公式之前，我们首先要讲解总平方和（Total Sum of Square，TSS）的概念。总平方和是和输出变量里的总方差成比例的，它的设计思路是，在进行回归之前，用它来衡量输出变量内在的变异性大小。TSS的计算公式是：

统计量背后的思想是，如果一个线性回归模型是对实际总体模型比较接近的拟合，它就应该能完整地获得输出中的所有方差。实际上，我们经常把统计量当做一个相对数值，用它来指明某个回归模型解释了输出变量的方差中多大的比例。当运用回归模型得到了输出变量的一个估计值时，可以看到，观测数据中的误差被称为残差，而RSS实际上是与预测值和输出函数真实值之间留下的差异成比例的。因此，可以把统计量（即线性回归模型所解释的输出y中方差的数量）定义为起始方差（TSS）和终结方差（RSS）之间的差值相对于这个起始方差（TSS）的比例。用公式表示，这个计算就是：

从这个公式我们可以看到，的范围在0和1之间。接近1的值表明良好的拟合，因为它意味着大部分输出变量里的方差已经被回归模型所解释。另一方面，一个较小的值表明模型里的误差中还有显著的方差，说明模型拟合得不够好。让我们来看看，对于这两个模型，
统计量是如何手工计算出来的：

compute_rsquared <- function(x, y){
  rss <- sum((x - y) ^ 2)
  tss <- sum((y - mean(y))^2)
  return(1 - (rss / tss))
}
compute_rsquared(machine_model1$fitted.values, machine_train$PRP)
compute_rsquared(cars_model2$fitted.values, cars_train$Price)

image.png

我们用到了lm()函数训练的模型的fitted.values属性，它是模型对于训练数据作出的预测。计算出的两个值都相当大，其中二手车模型又一次显示出了略微更好一些的拟合。现在我们看到了评价线性回归模型的两个重要衡量指标，即RSE和

统计量。现在，我们要考虑两个变量之间的线性关系是否还有一种更总体性的衡量指标，也可以运用到示例中。从统计学角度，我们可以想起相关系数的概念，它正好是描述这个问题的。
两个随机变量X和Y之间的相关系数（correlation）可以由下面的公式得出：

其实，在简单回归的情况下，输出变量和输入特征之间相关系数的平方就是统计量，这个结果进一步增强了后者作为一种有用的衡量指标的重要性。

2.4.4　比较不同的回归模型

当需要对用同一组输入特征训练的两个不同回归模型之间进行比较时，统计量就会非常有用。不过，我们还经常需要对输入特征数量并不相等的两个模型进行比较。例如，在特征选择的过程中，我们会需要知道把某个特征纳入模型是否是个好的思路。统计量的一个局限性是它对具有更多输入参数的模型往往会产生更大的值。

调整后的（adjusted ）试图纠正一个问题，即统计量对具有更多输入特征的模型总是会产生更大的值，因而容易受到过拟合的影响。调整后的总体上比本身更小，这是我们可以通过检查模型摘要里的值来检验的。调整后的的计算公式如下所示：

其中n和k的定义和在统计量里是一样的。现在，让我们在R语言里实现这个函数，并对我们的两个模型计算调整后的：

  n <- length(y)
  r2 <- compute_rsquared(x, y)
  return(1 - (1 - r2) * (n -1) / (n - k -1))
}
compute_adjusted_rsquared(machine_model1$fitted.values, machine_train$PRP, k_machine)
compute_adjusted_rsquared(cars_model2$fitted.values, cars_train$Price, k_cars)

image.png

另外还有几个常用的性能衡量指标也可以用来比较带有不同数量特征的模型。赤池信息准则（Akaike Information Criterion，AIC）使用了一种信息论方法，通过平衡模型的复杂性和精确度来评估模型的相对质量。在我们按方差最小化方法训练的线性回归模型上，它和另一个著名统计量—马洛斯Cp（Mallow抯 Cp）是成比例的，所以这两个性能衡量指标是可以互换使用的。第三个衡量指标是贝叶斯信息准则（Bayesian Information Criterion，BIC）。它和前两个衡量指标相比，对带有更多变量的模型往往会产生更不利的结果。

2.4.5　在测试集上的性能

到目前为止，我们在训练数据上观察了模型的性能。这对于判定一个线性模型能否很好地拟合数据有重要意义，但不会让我们对它处理未知数据的预测精确度有清晰的认识。为此，我们要转到测试数据集。要利用模型进行预测，可以调用predict()函数。这是R语言里的一个通用函数，有很多包扩展了它。对于用lm()训练过的模型，我们只需要提供模型和带有我们需要进行预测的观测数据的数据框即可：

machine_model1_predictions <- predict(machine_model1, machine_test)
cars_model2_predictions <- predict(cars_model2, cars_test)

下一步，要定义我们自己的函数，用来计算均方差（MSE）：

compute_mse <- function(predictions, actual){
  mean((predictions - actual)^2)
}
compute_mse(machine_model1$fitted.values, machine_train$PRP)
compute_mse(machine_model1_predictions, machine_test$PRP)
compute_mse(cars_model2$fitted.values, cars_train$Price)
compute_mse(cars_model2_predictions, cars_test$Price)

image.png

对于每个模型，我们已经调用了compute_mse()函数来返回训练和测试的均方差。在这个示例中，碰巧两个测试均方差的值都比训练均方差的值更小。测试均方差是略微大于还是略微小于训练均方差并不是特别重要的问题。重要的问题是测试均方差并没有显著大于训练均方差，因为测试均方差显著大于训练均方差就表明我们的模型对数据是存在过拟合的。注意，尤其是对于CPU模型，在原始数据集里的观测数据数量很少，这就导致测试集也是很小的。因此，就上述模型对于未知数据的预测性能而言，我们会在估计的精确度方面持保留态度，因为利用一个小的测试集作出的预测会具有更大的方差。