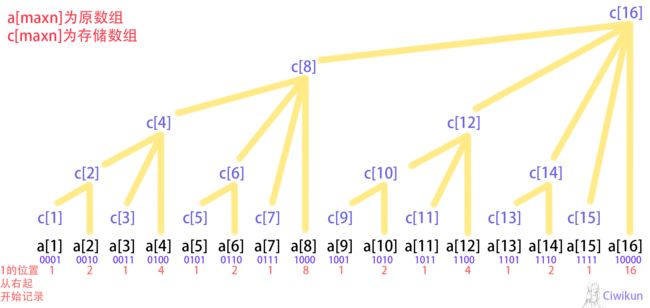
树状数组适用范围:给定区间,求最值,求和,区间单点修改。
与RMQ不同的是,RMQ一般只用作区间求最值。但在最值方面RMQ更加便捷。
从图上可以看出要找到c[i]的父节点只要用i+x(x为i转化为二进制从右起第一个出现1的位置)就可以了
寻找x可以通过lowbit函数,即通过计算机补码的巧用,x=i&(-i)
int lowbit(int x)
{
return x&(-x);
}
而每一个父节点存储的数据都是下面所有子节点的全部信息。对子节点修改就必定会对其所有的父节点进行更新,父节点c[i]下标的查找如下:
void update(int i, int x)
{
while(i<=n)
{
c[i]+=x;
i+=lowbit(i);//更新父节点
}
}
对于查找1~i的和、最大值、最小值可以表示为:
int sum(int i)
{
int res=0;
while(i>0)
{
res+=c[i];
i-=lowbit(i);
}
return res;
}
典型例题(模版):
HDU - 1166
对一个区域的数列进行查找、修改
#include
#include
using namespace std;
int c[50005];
int n;
int lowbit(int x)
{
return x&(-x);
}
void update(int i, int x)
{
while(i<=n)
{
c[i]+=x;
i+=lowbit(i);//更新父节点
}
}
int sum(int i)
{
int res=0;
while(i>0)
{
res+=c[i];
i-=lowbit(i);
}
return res;
}
int main()
{
int T, cnt;
scanf("%d", &T);
for(cnt=1; cnt<=T; cnt++)
{
int i, temp;
char op[10];
memset(c,0,sizeof(c));
scanf("%d", &n);
for(i=1 ;i<=n; i++)
{
scanf("%d", &temp);
update(i, temp);
}
printf("Case %d:\n", cnt);
while(~scanf("%s", op))
{
int l, r, k;
if(!strcmp(op,"End")) break;
if(!strcmp(op,"Query"))
{
scanf("%d%d", &l, &r);
printf("%d\n", sum(r)-sum(l-1));
}
if(!strcmp(op,"Add"))
{
scanf("%d%d", &k, &temp);
update(k, temp);
}
if(!strcmp(op,"Sub"))
{
scanf("%d%d", &k, &temp);
update(k, -temp);
}
}
}
return 0;
}
例题:POJ - 3928
题目大意:在数列X中找到a、b、c
满足a
#include
#include
using namespace std;
#define ll long long int
const int maxn = 1e5+7;
const int max_num = 1e5;
int a[maxn];
ll c[maxn];
int pos_west[maxn], pos_east[maxn], neg_west[maxn], neg_east[maxn];
int lowbit(int x)
{
return x&(-x);
}
void update(int i, int p)
{
while(i<=max_num)
{
c[i]+=p;
i+=lowbit(i);
}
}
ll getsum(int i)
{
int res=0;
while(i>0)
{
res+=c[i];
i-=lowbit(i);
}
return res;
}
void init()
{
memset(a,0,sizeof(a));
memset(c,0,sizeof(c));
memset(pos_west,0,sizeof(pos_west));
memset(pos_east,0,sizeof(pos_east));
memset(neg_west,0,sizeof(neg_west));
memset(neg_east,0,sizeof(neg_east));
}
int main()
{
int T;
scanf("%d", &T);
while(T--)
{
int i, n;
ll sum=0;
scanf("%d", &n);
init();
for(i=1; i<=n; i++)
{
scanf("%d", &a[i]);
update(a[i],1);
pos_west[i]=getsum(a[i]-1);
pos_east[i]=getsum(max_num)-getsum(a[i]);
}
memset(c,0,sizeof(c));
for(i=n; i>0; i--)
{
update(a[i],1);
neg_west[i]=getsum(a[i]-1);
neg_east[i]=getsum(max_num)-getsum(a[i]);
}
for(i=1; i<=n; i++)
{
sum+=pos_west[i]*neg_east[i]+neg_west[i]*pos_east[i];
}
printf("%I64d\n", sum);
}
return 0;
}
注:此方法还可以用来求取逆序数!!!
例题:HDU - 1556
给定区间,每次在这个区间加1,求每个点一共加了多少次1
思路:前缀和思想,如图
#include
#include
using namespace std;
int c[100005];
int n;
int lowbit(int x)
{
return x&(-x);
}
void update(int i, int p)
{
while(i<=n)
{
c[i]+=p;
i+=lowbit(i);
}
}
int getsum(int i)
{
int res=0;
while(i>0)
{
res+=c[i];
i-=lowbit(i);
}
return res;
}
int main()
{
while(~scanf("%d", &n)&&n)
{
int a, b;
memset(c,0,sizeof(c));
for(int i=1; i<=n; i++)
{
scanf("%d%d", &a, &b);
update(a, 1);
update(b+1, -1);
}
for(int i=1; i<=n; i++)
{
if(i!=1) printf(" ");
printf("%d", getsum(i));
}
printf("\n");
}
return 0;
}