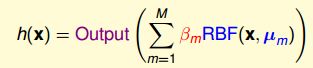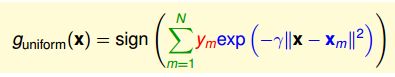RBF Network
前面的一篇SVM中,最后的分割函数:
Gaussian函数还有另外一个叫法——径向基函数,这是因为这个base function的结果只和计算这个x和中心点xn的距离有关,与其他的无关。
从其他方面来看SVM,先构造一个函数:
g(x) = y_nexp(-γ|x - x_n|^2) 指数求出来的其实就是x点和中心点的相似度,相似度越高,那么=晚y这个方向投票的票数就会越多。不同的g(x)有不同的权重,他们的线性组合就成了SVM,g(x)函数称为是radial function。所以Gaussian SVM就是把一些radial function联合起来做linear aggregation。
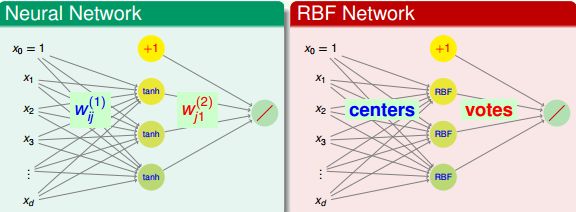
RBF Network就是SVM的延伸,目的就是找到所有radial hypotheses的linear aggregation,得到更好的网络模型。
可以看到这两种网络其实很类似,Neural Network的隐藏层是权值和数据做內积非线性转换再uniform的组合得到最后的输出,而对于RBF Network隐藏层是求高斯距离在做aggregation的方法。比较大的不同点就在于hidden层的不同了。
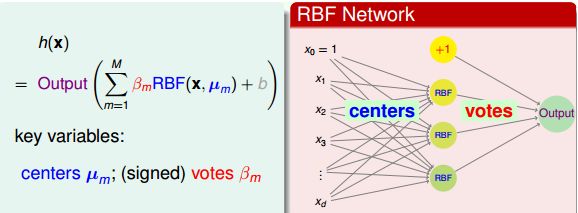
β就是每一个radial function的权值,μ就是中心点,m为中心点的个数,主要的,对比一下之前的SVM,β就是αy,μ就是支持向量。由于是一个分类问题,所以最后的output function就是sign函数了。
之前讲过,一个核函数不是随便乱选的,要满足两个条件:对称,半正定。对于SVM里面的核函数,其实ius把当前的数据提升到某一个很高很高的维度,然后做切片把数据分出来,polynomial function也是一样的,只不过是有限维度的。 而RBF其实就是在当前的空间做相似度处理,而那些kernel其实就是转换到z空间来计算核函数以表征两个向量的相似度。所以RBF和kernel都是衡量相似度的方式。虽然SVM和RBF Network都很相似,甚至可以说最后的决策函数基本一致的,但是他们的学习过程是很不一样的,一个是直接x空间,一个是转换到z空间。
衡量相似性并不止一种RBF方法,余弦相似度这些也可以衡量向量之间的相似度。
回过头来思考一下SVM,其实支持向量机就是先通过凸优化的一些方法找到有投票权利的点,之后给出相应的权值,最后决策就是这些有投票权利的点进行决策;对于其他线性模型,其实主要的不同就是他们每一个点都有投票的权利,这就导致很远的点都会干扰到边界。而RBF Network事实上做的事情和SVM有点像,因为RBF函数是指数增长,如果这个点很远的话会非常小,近乎就是0了,所以也起到了弱化远的点投票权,强化近的点投票权的能力。
RBF Network Learning
RBF Network的决策函数:
μ就是中心点,中心点是自己选择的。有一种选择中心点的方法,就是所有的点都作为中心点,那么每一个样本对于预测都会有影响,β就是影响的程度。如果影响的程度都是一样的,那么就是1了,β = 1*y,最后相乘做uniform aggregation之后sign得到结果。这种我们称为full RBF Network。
这个时候,full RBF Network就可以表示为:
这是一个指数函数,距离越远,那么衰减的就越快,x与中心点的距离越近那么就越大,距离越远就越小。也就是说,如果我们的样本点是N个,那么起了关键作用的一般就是最近的那个点而已,当然,不一定是最近的一个点,可以是最近的K个点,用这k个点来代替N个点,当前的点周围最近的k个点哪个类别最多,那么这个当前这个点就是属于哪个类别的。这种算法就叫K近邻算法。
k nearest neighbor通常比nearest neighbor model效果更好,计算量上也比full RBF Network要简单一些。值得一提的是,k nearest neighbor与full RBF Network都是比较“偷懒”的方法。因为它们在训练模型的时候比较简单,没有太多的运算,但是在测试的时候却要花费更多的力气,甚至可以说是几乎没有运算在里面,只需要做一些简单的数据处理即可,找出最相近的中心点,计算相对复杂一些。
如果是做回归问题,我们就只需要去掉output:
很明显,这样就是一个线性回归的问题了,每一个RBF 其实可以看做就是一个矩阵比如第一个元素x1,那么经过RBF的转换之后:
z_1 = [RBF(x_1,x_1), RBF(x_1, x_2), RBF(x_1,x_3),RBF(x_1,x_3)...RBF(x_1,x_N)]
那么Z就是z的按列排序了,按照线性回归的解公式:
β = (Z^TZ)^{-1}Z^Ty
上述矩阵Z是一个方阵,大小是N,有多少个中心点那么就有多少个N。如果每一个x都是不一样的,那么这个矩阵就是可以逆的矩阵了,毕竟x是训练数据,一样的就没有意义了。
化简一下:
β = Z^{-1}y
我们以x1为例子,那么解就是:
这个结果对于我们来说非常奇怪,如果这样的话那么对于所有的x都有:
g_{RBF}(x_n) = y_n所有Ein = 0,这样对于机器学习来说并不是一个好事情,因为这样很大概率会出现过拟合。当然,某些情况下还是很有用的,比如函数拟合或者是做autoencode。
为了避免过拟合,使用ridge regression的方法:
L2范式正则化。Z矩阵是由一系列Gaussian函数组成,每个Gaussian函数计算的是两个样本之间的distance similarity。这里的Z与之前我们介绍的Gaussian SVM中的kernel K是一致的。当时使用ridge regression得到的解:
比较一下kernel ridgeregression与regularized full RBF Network的β解,形式上相似但不完全相同。这是因为regularization不一样,在kernel ridgeregression中,是对无限多维的特征转换做regularization,而在regularized full RBF Network中,是对有限维(N维度)的特征转换做regularization。因此,两者的公式解有细微差别。
对于解决过拟合,还有另外的一种方法,可以选择K个具有代表性的点来代表这N个点,这样减少了中间点减少了权重的数量,VC维就减少了,可以起到regularization的作用。
原本的问题是求解中心点μ,β权重,现在β可以通过回归求解,那么只需要求μ了。
K Mean Algorithm
选择代表的原因,就是因为这些点有很高的相似性,所以可以使用一个中心点来代表,从所有的点中选择几个有代表性的点。
首先聚类算法是一种非监督的算法,不需要有label。需要确定的一般就是两个变量,分群值Sm,没一个分类可以表示为S1,S2,S3,S4...Sm,另一个就是中心值μm,μ1,μ2,μ3,μ4...μm,每一个分群就对应着中心,要求的就是这个中心。对于这类问题的优化,就可以使用square error function了。优化的步骤也是一样,求导,梯度下降或者梯度为0求最优值解。
刚刚也说过了,既然是衰减的形式,那么只需要取最大的就好了,最大也就意味着这需要求距离最近的即可。所以,表达式里面只有属于这个类别的数据求error。
最后就是求导做优化了:
两个变量组合的优化问题,通常的方法就是对这两个变量分别求。仔细观察一下这两个变量,可以发现,只要确定了μ,就可以确定S;或者只要确定了S,求个平均也可以得到μ。所以假设μ已经是固定的了,那么可以依次迭代x,和哪个μ的距离最小就属于哪个类别。
如果类别S是确定的,那么目标就是找到对应的μ中心点,显然这个,求个导的事,梯度下降就可以解决了。
所以这就成了一个鸡生蛋蛋生鸡的问题,所以一般一开始我们会选择随机的几个点作为中心μ,然后按照上诉步骤优化。
优化有结果吗?
这个优化的过程好像有些不一样,求导等于0应该是直接求出了最优的解,linear regression就是这个道理,但是为什么要一直这样迭代呢?这是因为求出来的这个μ并不是一个全局的μ,只是在当前对于每一个群S的一个最优,但是这个S并不是最优的,之前也说了:这个S和μ是互相牵制的,鸡生蛋蛋生鸡的问题,S可以得到μ,μ也可以得到S。所以整个过程通俗点就是通过μ求局部最优的S,通过S有球局部的最优μ,不断的迭代,慢慢的跑到全局。但是也没有可以跑到局部呢?这个是有可能的,这于初值有关,所以Kmean均值算法也是一个初值敏感的算法。对于局部这个问题,有一种解法就是可以合并最近的几个质心。事实上如果中心比较小,比如3个这样,一般都不会有局部出现,因为\sum_{m=1}^M(x_n - μ_m)^2不会这么的弯曲。
停止是一定的,因为无论是通过S优化μ还是μ优化S都朝Ein = 0为目的,如果Ein增加了是不会继续的,所以最后一定会到达一个平衡点。
The process of the RBF Network
既然中心有其他算法可以帮忙解决了,那么整个算法也就清晰了:
求解优化的过程中,可以使用validation来求解最优的λ和M。
RBF Network and KMeans in action
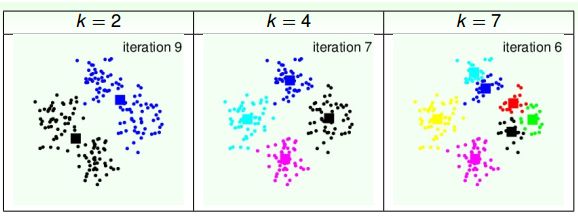
k值的大小和初始位置的不同都会影响聚类的结果。
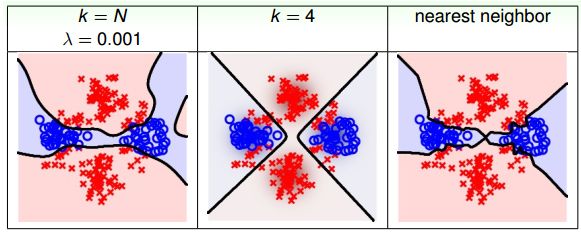
把这些机构k均值使用到RBF里面:
对于正则化也有不同的影响。
coding
KMeans
接下来就是代码实现KMeans算法了。KMeans算法其实很简单,首先随机得到几个中心点,根据中心点预测做聚类算法即可。
def loadDataSet():
'''loading data......'''
data = dataSet.load_iris()
dataset = data.data
target = data.target
PCA = pca.PCA(n_components=2)
dataset = PCA.fit_transform(dataset)
return np.mat(dataset), np.mat(target)
pass
加载数据,iris数据集进行降维操作便于可视化。
def distEclud(vecA, vecB):
'''calculate the distance from vecA to vecB'''
return np.sqrt(np.sum(np.power(vecA - vecB, 2)))
pass
def randCent(dataSet, k):
'''create the center'''
n = np.shape(dataSet)[1]
centroids = np.mat(np.zeros((k, n)))
for j in range(n):
minJ = np.min(dataSet[:, j])
rangeJ = float(max(dataSet[:, j]) - minJ)
centroids[:, j] = minJ + rangeJ * np.random.rand(k, 1)
return centroids
计算距离,随机选择中心点。随机选择中心点这里是先计算了每一个维度的范围,之后在这个范围里面随机选择。
def KMeans(dataSet, k, distMeas = tool.distEclud, createCent = tool.randCent):
'''KMeans Algorithm is running......'''
m = np.shape(dataSet)[0]
clusterAssment = np.mat(np.zeros((m, 2)))
centroids = createCent(dataSet, k)
clusterChanged = True
while clusterChanged:
clusterChanged = False
for i in range(m):
minDist = np.inf
minIndex = -1
for j in range(k):
distJI = distMeas(centroids[j,:], dataSet[i,:])
if distJI < minDist:
minDist = distJI
minIndex = j
if clusterAssment[i, 0] != minIndex:
clusterChanged = True
clusterAssment[i, :] = minIndex, minDist**2
for cent in range(k):
ptsInClust = dataSet[np.nonzero(clusterAssment[:, 0].A == cent)[0]]
centroids[cent, :] = np.mean(ptsInClust, axis=0)
dataFrame = pd.DataFrame(data=np.hstack((dataSet, clusterAssment[:,0])))
return dataFrame, centroids
选择和calculate distance的算法都是动态的方式,便于以后的改进。整个过程也比较简单,离哪个近就属于哪个类别。
RBF Network
①获取中心点
_,center = kMeans.KMeans(np.mat(x_train), k)
刚刚写好的KMeans就是这个作用。
②计算β值
beta = rbf(x_train, center, y_train, gama=gamma, lamda=lamda)
rbf函数的实现:
def rbf(x_train, center, y_train, gama = 0.001, lamda = 0.01):
M = center.shape[0]
N = len(x_train)
Z = np.zeros((M, N))
for i in range(M):
for j in range(N):
Z[i][j] = Gaussian(x_train[j], center[i], gama)
I1 = np.eye(N, k = 0)
beta = np.linalg.inv(np.dot(Z.T, Z) + lamda * I1)
beta = np.dot(beta, Z.T)
y_train = np.mat(y_train)
beta = np.dot(y_train, beta)
return beta
pass
def Gaussian(vecA, vecB, gama):
x_x = np.abs(np.sum(vecA - vecB))
x_x_2 = np.power(x_x, 2)
return np.exp(-1.0 * gama * x_x_2)
pass
首先是计算Z矩阵,就是φ(x)的矩阵。其实就是和上面步骤一模一样的,使用的是线性回归,β = (Z^TZ + λI)^{-1}Z^Ty使用直接就可以算,要是逻辑回归也是一样。
③预测
def predict(beta, x_train, center, gama):
result = []
for x in x_train:
x = np.mat(x)
sum = 0
for i, vecB in enumerate(center):
sum += beta[0,i]*Gaussian(x, vecB, gama)
result.append(sum)
return result
pass
为了方便调用,整合成一个函数:
def RBF(y_test, x_test, y_train, x_train, gamma = 0.001, lamda = 0.01, k = 4):
Again = True
while Again == True:
_,center = kMeans.KMeans(np.mat(x_train), k)
beta = rbf(x_train, center, y_train, gama=gamma, lamda=lamda)
Again = False
for i in range(beta.shape[1]):
if np.isnan(beta[0, i]):
Again = True
result = predict(beta, x_train, center, gamma)
for i in range(len(result)):
if result[i] > 0:
result[i] = 1
else:
result[i] = -1
posibility = 0
for i in range(len(result)):
if result[i] == y_train[i]:
posibility += 1
train_accuracy = posibility/len(result)
result = predict(beta, x_test, center, gamma)
for i in range(len(result)):
if result[i] > 0:
result[i] = 1
else:
result[i] = -1
posibility = 0
for i in range(len(result)):
if result[i] == y_test[i]:
posibility += 1
test_accuracy = posibility/len(result)
return train_accuracy, test_accuracy
可以计算不同gamma,lamda,k的影响。
④获取数据
def load_data():
data = dataset.load_breast_cancer().data
target = dataset.load_breast_cancer().target
for i in range(len(target)):
if target[i] == 0:
target[i] = -1
x_train, x_test, y_train, y_test = train_test_split(data, target, random_state=42, shuffle=True, test_size=0.4)
return x_train, x_test, y_train, y_test
pass
⑤启动函数
if __name__ == '__main__':
x_train, x_test, y_train, y_test = load_data()
gamma = [1,0.1,0.01,0.001,0.0001]
lamda = gamma
train_accuracy = []
test_accutacy = []
c = ['red', 'blue', 'orange', 'green', 'yellow', 'black']
for n, i in enumerate(gamma):
for j in lamda:
train, text = RBF(x_test=x_test, y_test=y_test, x_train=x_train, y_train=y_train, gamma=i, lamda=j)
print('gama : ',i, ' lamda : ', j, ' train_accuracy : ', train, ' text_accuray : ', text)
train_accuracy.append(train)
test_accutacy.append(text)
plt.plot(lamda, train_accuracy, c = c[n], label = 'gamma:'+str(i) + ' (train)')
plt.plot(lamda, test_accutacy, c = c[n], linestyle='--', label = 'gamma:'+str(i) + ' (test)')
plt.xlabel('lambda')
plt.ylabel('accuracy')
plt.legend(loc = 'upper right')
train_accuracy = []
test_accutacy = []
plt.show()
for n, i in enumerate(lamda):
for j in gamma:
train, text = RBF(x_test=x_test, y_test=y_test, x_train=x_train, y_train=y_train, gamma=j, lamda=i)
print('lamda : ',i, ' gama : ', j, ' train_accuracy : ', train, ' text_accuray : ', text)
train_accuracy.append(train)
test_accutacy.append(text)
plt.plot(gamma, train_accuracy, c = c[n], label = 'lamda:'+str(i) + ' (train)')
plt.plot(gamma, test_accutacy, c = c[n], linestyle='--', label = 'lamda:'+str(i) + ' (test)')
plt.xlabel('gamma')
plt.ylabel('accuracy')
plt.legend(loc = 'upper right')
train_accuracy = []
test_accutacy = []
plt.show()
ks = [2,3,4,5,6,7]
train_accuracy = []
test_accutacy = []
for i in range(6):
for n, i in enumerate(ks):
train, text = RBF(x_test=x_test, y_test=y_test, x_train=x_train, y_train=y_train, gamma=0.0001, lamda=0.01, k=i)
print('k == ' + str(i))
train_accuracy.append(train)
test_accutacy.append(text)
plt.plot(ks, train_accuracy, c = c[n], label = 'train')
plt.plot(ks, test_accutacy, c = c[n], linestyle='--', label = 'test')
plt.xlabel('the number of k')
plt.ylabel('accuracy')
plt.legend(loc = 'upper left')
plt.show()
train_accuracy = []
test_accutacy = []
pass
效果的讨论
在运行函数得到结果后进行分析。
①当γ固定了,看看lamda变化对于结果的影响。
其实还是很正常的,随着gamma的减少,准确率慢慢提上去了,虚线的测试数据,直线是准确率。Gaussian函数: g(x) = exp(-γ|x_n - μ|^2)γ越小, 就相当于σ变大,高斯函数的标准差变大那么这个函数就会变的更加平滑,泛化能力会很强。其实就是regularization的过程。
观察上图是可以得到λ对于整体的影响不会太大。基本是平缓的。
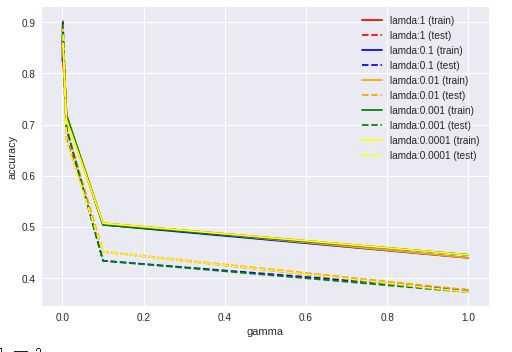
②当λ固定了,看看γ变化对于结果的影响。
γ越小效果越好,但是如果γ非常小,那么λ对于模型的影响几乎是没有影响。
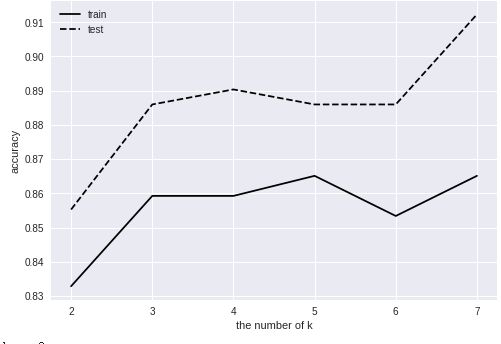
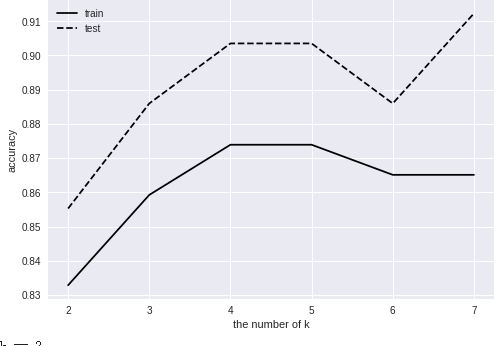
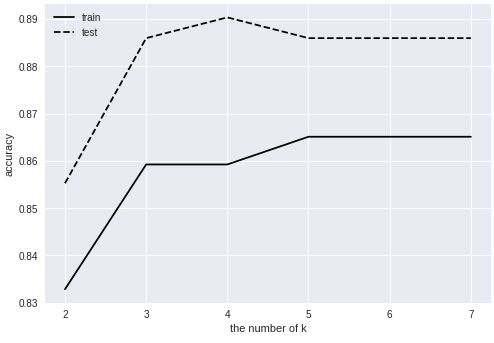
③对于k的数量和准确率的讨论
效果不太稳定,我多做了几次。
效果非常非常不稳定,我之前怀疑是线性回归的解不稳定的缘故,之前学习到病态矩阵,也就是近似奇异矩阵的矩阵,而regularization L2正则化就是为了使得病态矩阵转换成正常矩阵,所以增大了λ,显然并没有什么卵用。虽然整体效果不错。上面的结果就已经是λ增大的结果了。
所以最后还有两个问题没有解决,一个就是λ为什么对于模型的影响很很小,另一个上面没有提到,为什么测试数据的准确率会大于训练数据的准确率?这还打的明显,不知道是不是没有做交叉验证的结果,因为懒。。。。之前看到的解释是:
如果程序很好的实现了模型,那么就是模型不适合你的数据,因为这表明存在如下问题:每次训练,都使得训练之后的模型对测试的 1折效果很好,而对用于训练的9折效果惨淡,也就是模型落入了局部极值点而非全局极值点。这很有可能是模型在具体数据下的失效问题。
但是这个问题已经重复过了很多次,一直在使用test_train_split区分,同时也有shuffle。事实上在γ比较小的时候,测试数据就超过了训练数据的准确率,上面γ的变化可以看到。
最后附上GitHub代码:https://github.com/GreenArrow2017/MachineLearning/tree/master/MachineLearning/RBFNetwork