1. LR原理
逻辑回归是二分类模型,本质是线性分类器(wx+b=0)。但是,它将特征的线性组合作为自变量,然后利用sigmoid函数将其映射到(0,1)上,映射后的值是y=1的概率。
LR由条件概率分布P(Y|X)表示,Y=0,1,则有:
p(y=1|x)=exp(wx+b)/(1+exp(wx+b))
p(y=0|x)=1/(1+exp(wx+b))
所以由对数几率:
log(p)=log(p/(1-p))=wx
由上,我们可以得到输出y=1的对数几率是输入x的线性函数(即为逻辑斯蒂回归模型)
观察到:线性函数的值越接近正无穷,概率值就越接近1;线性函数的值越接近负无穷,概率值越接近0。
逻辑回归就是一种减小预测范围,将预测值限定为[0,1]间的一种回归模型。LR分类范围需要在[0,1]之内,在x=0附近比较敏感,在z>>0或z<<0处,都不敏感。而线性回归LR'在整个实数域内敏感度一致。
2. 模型参数估计
在统计学中,常常使用极大似然估计法来求解,即找到一组参数,使得在这组参数下,我们的数据的似然度(概率)最大。
则有:L(w)= (yi*logp(y=1|xi)+(1-yi)*(1-log(y=1|xi)))
求L(w)最大值,得到w的估计值
在逻辑回归模型中,我们最大化似然函数和最小化对数似然损失函数实际上是等价的。逻辑回归学习中通常采用的方法是梯度下降法 和 牛顿法。
3. 逻辑回归正则化
当模型参数过多时,往往会出现过拟合现象,为了避免过拟合,我们需要在损失函数(经验风险项)中引入正则化项(结构风险最小化的一种实现形式)。
L1范数:是指向量中各个元素绝对值之和,也有个美称叫“稀疏规则算子”(Lasso regularization)。那么,参数稀疏有什么好处呢?
L1可以自动进行特征选择。一般情况下,很多特征x与y没有多大联系。当我们在损失函数中考虑到这些特征时,虽然可以降低训练误差,但是当新的样本出现,这些没有携带多少信息的特征就会干扰预测正确结果y。因此引入了稀疏规则算子进行特征选择,去掉这些没多大信息的特征,即把这些特征的权重置为0。
L2范数:它有两个美称,在回归里面,有人把有它的回归叫“岭回归”(Ridge Regression),有人也叫它“权值衰减”(weight decay)。
L2可以解决过拟合问题。相比于L1将没有信息的特征权重置为0,L2是将那些没有信息的特征权重接近于0,而不等于0。我们知道:模型参数越小,表示模型越简单,就越不容易过拟合。为甚么模型参数越小,模型就越不容易过拟合?可能是因为,参数越小,这个特征对模型预测的影响越小,不会出现偏见情况。
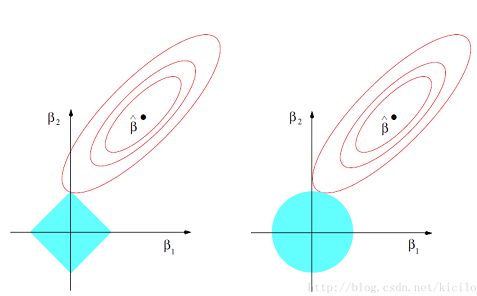
结合下图,左边为L1,右边为L2,圆形为等高线:
上图中实心的黑点是真实的损失函数(不带有正则项的部分),我们叫做原问题的最优解。
红圈就是系数、在原问题下可能的解的范围,蓝色的实心圈是正则项约束的可能的解的范围。如果两个函数要是有共同的解,那么在几何意义下或者说从几何图形上来看,这两个函数的图像所在范围是要有共同交点或者要有交集。由于Lasso Regression或者Ridge Regression的整个Loss Function也就是我们的目标函数是由原问题和正则项两部分构成的,那么如果这个目标函数要有解并且是最小解的话,原问题和正则项就要有一个切点,这个切点就是原问题和正则项都满足各自解所在范围下的共同的解。
当红圈从图中的实心黑点不断往外变化与蓝色实心圈相切的时候,在L1正则情况下,我们第一次解相遇在坐标轴上的点(即有某个特征的权重为0),而L2第一次相遇的点则更趋向于接近坐标轴的点(特征权重接近0),这就是为什么L1可以导致稀疏。
4. 逻辑回归与最大熵模型MaxEnt(softmax)的关系?
LR与MaxEnt都是对数线性模型,LR解决二分类问题,MaxEnt是其扩展模型,解决多分类问题。
逻辑回归跟最大熵模型没有本质区别。逻辑回归是最大熵对应类别为二类时的特殊情况
指数簇分布的最大熵等价于其指数形式的最大似然。
二项式分布的最大熵解等价于二项式指数形式(sigmoid)的最大似然;
多项式分布的最大熵等价于多项式分布指数形式(softmax)的最大似然。
5. 优缺点及适用场景
优:计算代价低,易于理解与实现;防止过拟合和欠拟合。
缺:容易欠拟合,分类精度不太好
适用场景:用于二分类问题, 比如垃圾邮件判断(是/否垃圾邮件),是否患某种疾病(是/否), 广告是否点击等场景。