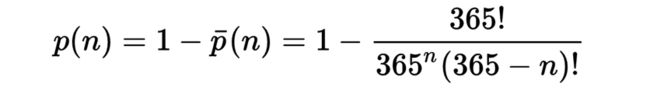生日悖论
相信很多人都有过以下类似的经历:每逢过年,都会有各种各样的同学聚会。就在那个微信和红包还没有盛行的年代,这种聚会的形式大多以聚餐、唱K、喝茶的形式呈现。一般此类活动都由班长召集,因为只有他那里有最原始的同学档案(从生日、血型到家庭住址一应俱全),每次翻阅同学录,他都会有一些意外发现,譬如某人和某人竟然是同年同月同日生的,那种感觉就像哥伦布发现了新大陆一样。
后来终于有一年,某位热心的同学把这些资料输入了excel。通过按出生日期排序,很容易就能识别出在同一天出生的同学,于是在饭桌上就有好事之徒开始乱点鸳鸯谱。最常见的段子便是:“某A和某B,你看你们俩生日都是同一天,这是多么难得的缘分呐,1/365的概率啊,你们俩不处对象可真是太可惜了!”除了当事人一脸懵逼以外,其他同学多是为这位同学的机智而乘机起哄。倒是鲜有人去质疑这位同学脱口而出的1/365的概率是否合理。
不久前我从一本书上读到这样一个有趣的试验,请问:
一个房间内有23个人,任意两人生日同一天的概率有多少?
答案大大出乎常人的意料,甚至可以用反直觉来形容。
你一定很好奇,正确的答案到底是多少呢?是50%。
“不会吧,有那么高么?”我已经听到了你心中的质疑。不急,我们看看这道概率计算题是怎么算的。
对于一个23人的房间,先考虑问题的补集:23人生日两两不同的概率是多少?为此,我们可以让23个人依次进入房间,那么每个人生日都与其他人不同的概率依次是1, 364/365, 363/365, 362/365, 361/365,等等。先进入房间的这些人生日两两不同的概率是很大的,比如说前面5个是1×364/365×363/365×362/365×361/365=97.3%。而对于最后进入房间的几个人情况就完全不同。最后几个人进入房间并且找不到同生日者的概率是… 345/365, 344/365, 343/365。
用阶乘可以写成如下形式:
p(n)表示n个人中至少2人生日相同的概率
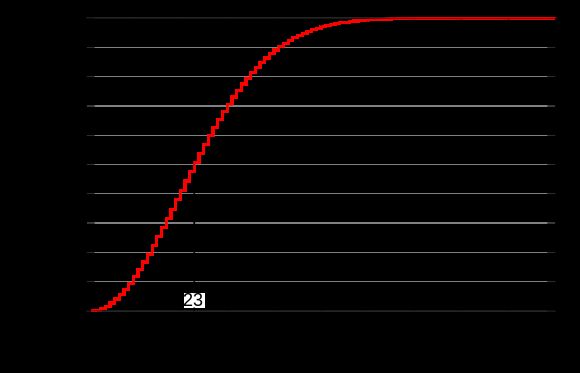
用图表示如下:
这样看来,一个23人的房间里2人生日相同的概率就已经达到50%,那么,一个50-60人的班里面出现同一天生日的同学就不足为奇了。看完这个例子,我想你已经发现了,在生活中一些我们坚信认为正确的判断,未必如你想的那么正确,这里面存在认知偏差,我们缺乏深入思考。
我们的知识在增长, 但它受到自信增长的威胁,它增长了我们的知识, 同时也增加了疑惑、无知和自负。
捷径
我家和父母家很近,每次去我父母那儿蹭饭,都会穿过我家小区的中央花园,从南门出,横穿过一条马路,就是父母家所在的小区。走过小区中央花园会有一个花圃,用不规则大石块铺成的小径引导你来到通往南门主路上,在我看来这是一条捷径。
这条路线我走了不知多少回,但从来没思考过一个问题,我去和回来走的是不是同一条路?
直到有一天中午,我发现花农在我经常走的这条小径两侧补种一些高羊茅(一种冷季型草坪草)。但当我回来再次穿过习以为常的小径时,却没有找到那些新种下的高羊茅。当时也没细想,只是下意识地在心中开始编造一些自认为合理的可能性,“难道花农觉得栽下去不好看又都拔走了?”
第二天,再次徒步来到这条小径,发现那些高羊茅整齐地排列在小径两侧。这回我是彻底迷糊了,要是换作以前,可能会迷信地认为是传说中的“鬼打墙”。为了查个究竟我决定这次不从这条小径穿过花圃,于是我又继续往前走了一段,绕过一个S型的树丛后终于找到了一条看似一模一样的小径,唯一的区别是刚才经过那条小径两侧有高羊茅,而这条没有。这下我才恍然大悟,原来我每次去父母家走的是前面那条小径A,回来走的是这条小径B,他们看起来很像,都是横穿整个花圃,只是中间隔了几棵树,不易被一眼发现而已。
我并没有止步于这个“重大发现”,而是开始恐慌,我在这小区都住了快5年了,为什么直到今天才察觉这个“秘密”呢?明明就在我眼皮底下的事儿,我却被蒙蔽了那么久,那生活中是不是还有很多其他的事情也一样违背我的直觉,只是我并不知道还有多少?以及它们在哪里?还是会像这次这样猛然醒悟?
进而,我又开始思考,为什么我总是习惯于从A进B出呢?而从来没有考虑过往前多走几步也许我就会发现可以B进A出,或者A进A出,B进B出呢?2的平方是4,起码有四种方案可供我选择,如果纯粹从距离远近的角度看待这个问题,它们的距离毕竟是一样的啊!
为了挑战我的直觉,我开始刻意改变路线,每次去时看到第一条小径A准备拐弯的时候,我就把这个念头强压下去。继续往前走几步,从以往回来的那条小径B穿过,回来的时候也刻意走A这条路线。这个过程其实很违背直觉,明明眼前有捷径你不走,非要走那条不易被发现的路。虽然我知道花在两条路线上的时间是一样的,但是我的大脑就是想走那条显而易见的路。
你以为你找到了一条捷径,可那只是通往终点的其中一条路而已,你被大脑欺骗了。
我一直想找到上述问题的答案,终于在Nassim Nicholas Taleb的《The Black Swan》这本书里找到了令人满意的解释。
研究者把我们的推理行为(大致)分为两种思维模式,分别称为“系统1”和“系统2”,或者“经验模式”和“认知模式”。二者的差别是显而易见的。
系统1,经验模式,是不费力的、自动的、快速的、模糊的(我们不知道我们在使用它)、平行的、易出错的。它就是所谓的“直觉”,以很快的速度发挥着作用。系统1是高度情绪化的,它反应迅速。它制造捷径,人们称之为“启发学”,它使我们能够快速地采取行动。毫无疑问,这些捷径是有效的,因为它们快,但有时会导致我们犯严重的错误。
系统2,认知模式,就是我们通常所称的思考。你经常在教室里使用它,因为它是费力的、有条理的、缓慢的、有逻辑的、连续的、渐进的、有自我意识的(你可以觉察推理的推进)。它犯的错比经验模式少,因为你知道结果是如何得来的,你能够返回你的思考步骤,对他们进行适应性修正。
我们的大部分推理错误来自当我们以为自己在使用系统2,而实际上却在使用系统1时。为什么?因为我们的反应是不经过思考和反省的,而系统1的主要特点就是我们对它的使用是无意识的!
人性的很多麻烦在于我们无法充分使用认知模式。
反思
曾经有一位20岁出头的大学生,对我说她有一项技能,我好奇地问是什么技能?她说:“我看人一向很准。”我当时听了就乐了,开玩笑地问:“哦?怎么个准法?”她很自信地说:“反正就是很准,从没看走过眼。”我没有再继续问下去也没有反驳她,只是微微冲她一笑:“你可真厉害,什么时候教教我呗?”
一只老母鸡,被养了三年,它总结出了过去1000天的经验:主人对我真好,每次伸过手来都是喂我好吃的。但第三年过年那一天,即第1001天,一直伸过来喂它的手,却抓住了它的脖子,把它摔死了,它成了春节餐桌上的清炖老母鸡。
一个真实的中国股市版是,2014年7月7日到2015年6月8日,中国股市上证指数从2033点涨到最高5178点,一年内股市连续上涨2.5倍多,当所有人都总结出股市还会继续上涨,会涨到6000点甚至10000点,2007年甚嚣尘上的黄金十年会涨到两万五千点的言论又开始不绝于耳。紧接着,一直黑天鹅出现了,股市开始暴跌,连续多日上演千股跌停。不得已之下,中国证监会不得不启动熔断机制,仅仅两月就跌到2851点,那些根据过去1年股指上涨2倍预期未来会继续大涨的人,如同那只养了1000天却在第1001天成了美餐的鸡,被股市这只原来一直给他们送钱的手一下了拿走了所有过去赚的钱和很多本钱。
人类在对随机事件的认识上容易犯不对称的错误。我们把成功归因于能力,把失败归因于在我们控制之外的事物,比如随机性。
当我们观察过去,然后得出关于未来的规律。根据过去预测未来的问题可能比我们已经讨论的问题还要严重,因为相同的过去的数据既可以证明一个理论,又可以同时证明完全相反的理论。如果你明天还活着,这可能意味着你可能长生不老,或者你更接近死亡。两个结论依赖于完全相同的数据。如果你是一只被喂养了很长时间的火鸡,你可以要么天真地以为喂食 证明你是安全的,或者聪明地知道它证明了你最后成为晚餐的危险。
在一个充满未知的世界,一味地依赖过去的经验和直觉做出判断,并以此来指导我们的行为,真的是件相当可怕的事情。
很多时候,我们冒险通常不是出于自信,而是出于无知和对不确定性的无视!
在一半时间里,我愿意成为一名怀疑主义者,与直觉作抗争;在另一半时间里,我笃信地做着不被别人看好的事情。
在一半的时间里,我讨厌不确定性;在另一半时间里,我热爱意外的好运。
在一半的时间里我选择保守行事;另一半时间里我勇于冒险。只不过我在其他人冒险的地方实行保守主义,在其他人谨慎的地方冒险。