第九章双变量回归与相关

x2yline
r Sys.Date()

知识清单

直线回归
- 相关概念
- 求法
- 统计推断
- 区间估计
直线相关
- 相关概念
- 求法
- 统计推断
- 决定系数
直线回归应用注意事项
秩相关
两回归直线的比较
曲线拟合

1. 直线回归

1.1 基本概念

用途
- 不是前几章的单变量，而是两个变量的关系
- 数值变量或有序分类变量（秩相关）
直线方程及各值含义
- 方程 1
  [
  \hat{y}=a=bX
  ]
- 方程 2
  [
  \mu_{Y|X}=\alpha+\beta X
  ]
  - $\hat{y}$表示X对应Y的总体均数$\mu_{Y|X}$的一个样本估计，称预测值
  - a、b分别为$\alpha$和$\beta$的样本估计，a称为常数项，b称回归系数
  - b的统计意义是当X变化一个单位时Y的平均改变的估计值

1.2 计算方法

1.2.1 理论计算

根据实测值Y与假定回归直线上的估计值$\hat{y}$的纵向距离$Y-\hat{y}$（残差）的平方和最小即最小二乘法可以推出
[
b=\frac{l_{XY}}{l_{XX}}=\frac{\sum{}{}(X-\bar{X})(Y-\bar{Y})}{\sum{}{}(X-\bar{X})^{2})}
]

[
a=\bar{Y}-b\bar{X}
]
式中$l_{XY}$为X与Y的离均差交叉乘积和，简称离均差积和

1.2.2 R语言计算

data9_1 <- haven::read_sav(
  file="E:\\医学统计学（第4版）\\各章例题SPSS数据文件\\例09-01.sav")
colnames(data9_1) <- c("age", "conc")
head(data9_1)

## # A tibble: 6 x 2
##     age  conc
##    
## 1    13  3.54
## 2    11  3.01
## 3     9  3.09
## 4     6  2.48
## 5     8  2.56
## 6    10  3.36

line.model <- lm(conc~age, data=data9_1)
print(line.model)

## 
## Call:
## lm(formula = conc ~ age, data = data9_1)
## 
## Coefficients:
## (Intercept)          age  
##      1.6617       0.1392

line.model_summary <- summary(line.model)

1.3 统计推断

H0：$\beta=0$，即两变量直接无直线关系
H1：$\beta \neq 0$，即两变量之间有线性关系

1.3.1 方差分析

公式

把Y的离均差平方和进行分解，分为回归平方和与残差平方和，其自由度分别为1，n-2。
[
Y-\bar{Y}=Y-\hat{Y}+\hat{Y}-\bar{Y}
]
[
\sum{}{}(Y-\bar{Y})^{{2}=\sum{}{}(\hat{y}-\bar{Y})}{2} + \sum{}{}(Y-\hat{y})^{2}
]
[
SS_{总}=SS_{回}+SS_{残}
]

F值计算公式为（单侧F检验）：

[
F=\frac{SS_{回}/\nu_{回}}{SS_{残}/\nu_{残}},\ \nu_{回}=1,\ \nu_{残}=n-2
]

$SS_{回}$计算公式可以化简为：

[
SS_{回}=bl_{XY}=\frac{l_{XY}^{{2}}{l_{XX}}=b}{2}l_{XX}
]

R语言实现

手动计算

# 残差平方和
ss2 <- sum(line.model$residuals^2)
# 离均差平方和
ss0 <- var(data9_1$conc)*(nrow(data9_1)-1)
# 回归平方和
ss1 <- ss0-ss2
# F统计量
f.statistic <- (ss1/1)/(ss2/(nrow(data9_1)-2))
# p值
p <- pf(f.statistic, lower.tail=FALSE, df1=1, df2=nrow(data9_1)-2)
cat("F statistic is ", f.statistic, "\np value is ", p, sep="")

## F statistic is 20.96842
## p value is 0.003773985

直接调用查看summary.lm对象里的f值并转为p值

f_df1_df2 <- summary(line.model)$fstatistic
p_value <- pf(f_df1_df2[1], df1=f_df1_df2[2], df2=f_df1_df2[3], lower.tail=F)
cat(cat("F statistic is ", f_df1_df2[1], "\np value is ", p_value, sep=""))

## F statistic is 20.96842
## p value is 0.003773985

直接打印sammary.lm对象，最后一行信息即为其F值和对应p值

summary(lm(conc~age, data=data9_1))

## 
## Call:
## lm(formula = conc ~ age, data = data9_1)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.21500 -0.15937 -0.00125  0.09583  0.30667 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)   
## (Intercept)  1.66167    0.29700   5.595  0.00139 **
## age          0.13917    0.03039   4.579  0.00377 **
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.197 on 6 degrees of freedom
## Multiple R-squared:  0.7775, Adjusted R-squared:  0.7404 
## F-statistic: 20.97 on 1 and 6 DF,  p-value: 0.003774

1.3.2 t检验

t值计算公式：
[
t=\frac{b-0}{S_{b}},\ \nu=n-2
]

[
S_{b}=\frac{S_{Y\cdot X}}{\sqrt{l_{XX}}}
]

[
S_{Y\cdot X}=\sqrt{\frac{SS_{残}}{n-2}}
]

$S_{Y\cdot X}$为回归的剩余标准差，化简后有：

[
\sqrt{F}=t
]

R语言实现（双侧t检验）：

lxx <- var(data9_1$age)*(nrow(data9_1)-1)
Sb <- sqrt(sum(line.model$residuals^2)/(nrow(data9_1)-2))/(sqrt(lxx))
t_statistic <- (line.model$coefficients[2]-0)/Sb
cat("t statistic is ", t_statistic, "\np value is ", 
    2*pt(t_statistic, df=nrow(data9_1)-2, lower.tail=FALSE),
    sep="")

## t statistic is 4.579129
## p value is 0.003773985

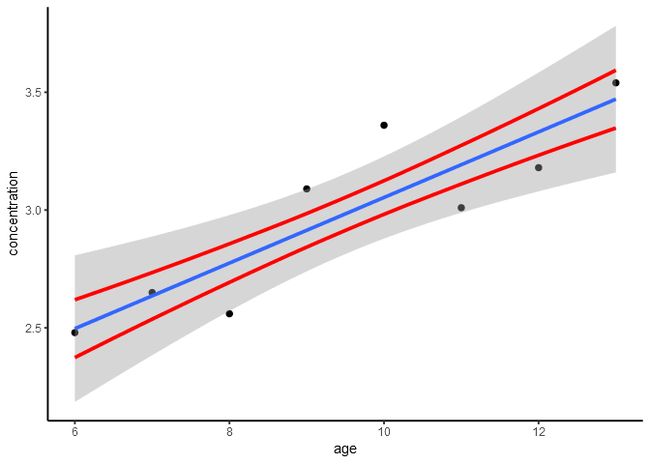
1.3.3 区间估计

总体回归系数$\beta$的可信区间
表示Y0的均数95%的置信区间

结合上述t检验的公式，$\beta$的$1-\alpha$可信区间为：
[
b\pm t_{\alpha/2,\ \nu}\cdot S_{b}
]

总体均数$\mu$的可信区间

$\hat{Y0}$会因样本（拟合的曲线）而异，其抽样误差大小的标准误：

[
S_{\hat{Y_{0}}}=S_{Y\cdot X}\sqrt{\frac{1}{n}+\frac{(X_{0}-\bar{X})^{{2}}{\sum{}{}(X-\bar{X})}{2}}}
]

$\mu_{Y|X0}$的置信区间为：

[
\hat{Y_{0}} \pm t_{\alpha/2,\ \nu}\cdot S_{\hat{Y_{0}}}
]
R语言实现：

lxx <- var(data9_1$age)*(nrow(data9_1)-1)
# 剩余标准差
syx <- sqrt(sum(line.model$residuals^2)/(nrow(data9_1)-2))
Sb <- syx/(sqrt(lxx))
t_statistic <- (line.model$coefficients[2]-0)/Sb

Sy01 <- syx*sqrt(1/nrow(data9_1)+
              (data9_1$age-mean(data9_1$age))^2/
              (var(data9_1$age)*nrow(data9_1)-1))

# geom_smooth自动加上了标准偏差即se=TRUE
library(ggplot2)
p <- ggplot(data9_1, aes(age, conc))+
  xlab("age")+ ylab("concentration")+
  geom_point(size=1.5)+
  geom_smooth(method="lm", se=TRUE)+
  theme_classic()
print(p)

p <- p + geom_smooth(aes(x=age, y=Sy01+
                   age*line.model$coefficients[2]+
                   line.model$coefficients[1]), color="red",
              se=FALSE, method="loess")+
  geom_smooth(aes(x=age, y=-Sy01+
                    age*line.model$coefficients[2]+
                    line.model$coefficients[1]), color="red",
              se=FALSE, method="loess")

print(p)

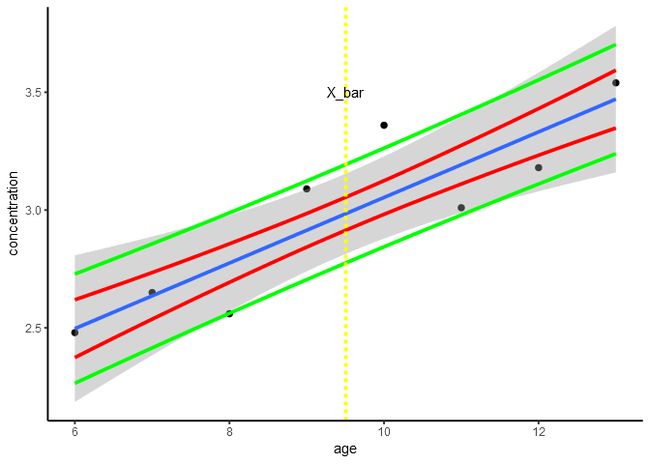
个体Y值的预测区间
表示Y0值的95%置信区间范围
[
S_{Y_{0}}=S_{Y\cdot X}\sqrt{1+\frac{1}{n}+\frac{(X_{0}-\bar{X})^{{2}}{\sum{}{}(X-\bar{X})}{2}}}
]

R语言实现：

lxx <- var(data9_1$age)*(nrow(data9_1)-1)
# 剩余标准差
syx <- sqrt(sum(line.model$residuals^2)/(nrow(data9_1)-2))
Sb <- syx/(sqrt(lxx))
t_statistic <- (line.model$coefficients[2]-0)/Sb

Sy02 <- syx*sqrt(1+1/nrow(data9_1)+
              (data9_1$age-mean(data9_1$age))^2/
              (var(data9_1$age)*nrow(data9_1)-1))

p + geom_smooth(aes(x=age, y=Sy02+
                   age*line.model$coefficients[2]+
                   line.model$coefficients[1]), color="green",
              se=FALSE, method="loess")+
  geom_smooth(aes(x=age, y=-Sy02+
                    age*line.model$coefficients[2]+
                    line.model$coefficients[1]), color="green",
              se=FALSE, method="loess")+
  geom_vline(xintercept=mean(data9_1$age), lwd=1, color="yellow", linetype=2)+
  annotate("text", x=mean(data9_1$age), y=3.5, label="X_bar")+
  guides(color = guide_legend(title = "LEFT", title.position = "left"))

2. 直线相关

2.1 相关概念

又称简单相关，用于双变量正态分布
相关系数（coefficient of correlation）又称Pearson积差相关系数（coefficient of product-moment correlation），符号$r$代表样本相关系数，符号$p$代表总体相关系数。

2.2 计算公式

以符号$r$表示样本相关系数，符号$\rho$表示总体相关系数，$r$是$rho$的估计，与b不同，它没有单位
[
r=\frac{\sum{}{}(X-\bar{X})(Y-\bar{Y})}{\sqrt{\sum{}{}(X-\bar(X))^{{2}}\sqrt{\sum{}{}(Y-\bar{Y})}{2}}}=\frac{l_{XY}}{\sqrt{l_{XY}l_{YY}}}
]

R语言实现：

data9_5 <- haven::read_sav(
  file="E:\\医学统计学（第4版）\\各章例题SPSS数据文件\\例09-05.sav")
colnames(data9_5) <- c("number", "age", "v")
# 公式法
r <- sum((data9_5$age-mean(data9_5$age))*(data9_5$v-mean(data9_5$v)))/
  sqrt(var(data9_5$age)*(nrow(data9_5)-1)*var(data9_5$v)*(nrow(data9_5)-1))
print(r)

## [1] 0.8754315

# 包法
cor(data9_5$age, data9_5$v)

## [1] 0.8754315

2.3 统计推断

2.3.1 t检验

H0：$\rho=0$
[
S_{r}=\sqrt{\frac{1-r^{2}}{n-2}},\ \nu=n-2
]
[
t=\frac{r-0}{S_{r}}
]

R语言实现：

# 方法1：
Sr <- sqrt((1-r^2)/(nrow(data9_5)-2))
t_statistic <- (r-0)/Sr
pt(t_statistic, lower.tail=FALSE, df=nrow(data9_5)-2)*2

## [1] 1.910939e-05

# 方法2：
cor.test(data9_5$v, data9_5$age)

## 
##  Pearson's product-moment correlation
## 
## data:  data9_5$v and data9_5$age
## t = 6.5304, df = 13, p-value = 1.911e-05
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.6584522 0.9580540
## sample estimates:
##       cor 
## 0.8754315

2.3.2 可信区间

由于相关系数的抽样分布在$\rho$不等于0的情况下呈偏态分布，所以不能用t分布直接计算，向进行变量变换，使其服从正态分布在计算可信区间

对r作z反双曲正切函数变换：
[
z=tanh^{-1}r或z=\frac{1}{2}ln\frac{1+r}{1-r}
]
近似计算z的可信区间
[(z-u_{\alpha/2/\sqrt{n-3}},\ z+u_{\alpha/2/\sqrt{n-3}})
]
变换z为r
[
r=tanhz或r=\frac{e^{2z}-1}{e{2z}+1}
]

R语言实现

# 方法1：
z <- atanh(r)
u_0.05_2 <- qnorm(0.975, mean=0, sd=1)
r1 <- tanh(z-u_0.05_2/sqrt(nrow(data9_5)-3))
r2 <- tanh(z+u_0.05_2/sqrt(nrow(data9_5)-3))
cat("CL is ", r1, "~", r2, sep="")

## CL is 0.6584522~0.958054

# 方法2：
cor.test(data9_5$age, data9_5$v, conf.level=0.95, alternative="two.sided")

## 
##  Pearson's product-moment correlation
## 
## data:  data9_5$age and data9_5$v
## t = 6.5304, df = 13, p-value = 1.911e-05
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.6584522 0.9580540
## sample estimates:
##       cor 
## 0.8754315

2.4 决定系数

定义：回归平方和与总平方和之比，计算公式为

[
R^{{2}=\frac{SS_{回}}{SS_{总}}=\frac{l_{XY}}{2}/l_{XX}}{l_{YY}}
]
对于双变量回归分析，$R^{2}$即$r{2}$，处可以概括拟合效果外，还可以作假设检验

[
F=\frac{R^{2}}{(1-R{2})(n-2)}=\frac{SS_{回}}{SS_{残}/\nu_{残}}=\frac{MS_{回}}{MS_{残}}
]

R语言实现：

data9_5 <- haven::read_sav(
  file="E:\\医学统计学（第4版）\\各章例题SPSS数据文件\\例09-05.sav")
colnames(data9_5) <- c("number", "age", "v")
line.model <- lm(v~age, data=data9_5)
r.squared <- summary(line.model)$r.squared
print(r.squared)

## [1] 0.7663803

adj.r.squared <- summary(line.model)$adj.r.squared
print(adj.r.squared)

## [1] 0.7484095

r.squared <- 1-var(line.model$residuals)*(nrow(data9_5)-1)/
  (var(data9_5$v)*(nrow(data9_5)-1))
print(r.squared)

## [1] 0.7663803

f.statistic <- (r.squared)/((1-r.squared)/(nrow(data9_5)-2))
print(f.statistic)

## [1] 42.64598

summary(line.model)$fstatistic

##    value    numdf    dendf 
## 42.64598  1.00000 13.00000

3. 直线回归应用注意事项

根据目的选择变量及统计方法（自变量和因变量，如重测信度评价的相关系数，r应达到0.40以上
进行相关，回归分析前应绘制散点图，离群值
结果解释
- 相关系数或回归系数的绝对值反映密切程度
- p值越小越有理由认为变量间的直线关系存在
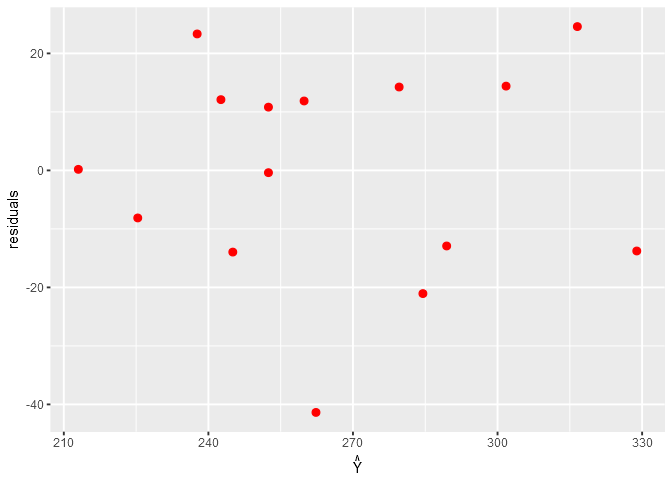
残差图观察是否符合模型假设的条件：自变量与因变量关系为线性，误差服从均数为0的正态分布，且方差相等，各观测独立(残差图横坐标为$\hat{Y}$或者X，纵坐标为残差)
- 正常为在y=0处对称分布，并且左右对称
- 离群值会与群体远离
- 喇叭状（左右不对称）说明方差不齐（须稳定化处理）
- 呈曲线则可能是符合曲线模型
- 呈直线说明残差与时间存在相关
R语言实现残差图

data9_5 <- haven::read_sav(
  file="E:\\医学统计学（第4版）\\各章例题SPSS数据文件\\例09-05.sav")
colnames(data9_5) <- c("number", "age", "v")
line.model <- lm(v~age, data=data9_5)
# +geom_point(aes(age, v), size=1.5)+
#   geom_smooth(aes(age, v), method="lm")+
library(ggplot2)
ggplot(data9_5)+
  geom_point(aes(x=predict(line.model), y=residuals(line.model)), color="red", size=2)+
  ylab("residuals")+xlab(latex2exp::TeX("$\\hat{Y}$"))

残差图没有明显的偏倚趋势（各区域残差的变异程度大致相同），说明残差至少在一定的范围内是恒定的，该线性模型的效果基本还行

4. 秩相关

4.1 适用条件

不服从双变量正态分布，而不宜做积差相关分析（散点图或统计表看出）

总体分布类型未知

原始数据用等级表示

4.2 Spearman秩相关

等级相关系数公式

$d$是指两个变量的秩差，完全正相关则$\sum{}{}d_{i}^{{2}$有最小值为0，完全负相关则$\sum{}{}d_{i}}{2}$有最大值为$\frac{n(n^{{2}-1}{3}$，0相关则则$\sum{}{}d_{i}}{2}=\frac{0+\frac{n(n^{{2}-1}{3}}{2}=\frac{n(n}{2}-1}{6}$，有以下公式

[
r_{s}=1-\frac{6\sum{}{}d^{2}}{n(n{2}-1)}
]

$r_{s}$介于-1与1之间，负数则为负相关，正数则为正相关，0则0相关

统计推断

样本等级相关系数$r_{s}$是总体相关系数$\rho_{s}$的估计值，检验$\rho_{s}$是否不为0可以用查表法，如果n大于50，可以用u检验，其中$u=r_{s}\sqrt{n-1}$，查u界值确定p

相同秩较多的情况下，需要校正，也可以不校正直接进行秩的pearson相关系数的计算

R语言实现

data9_8 <- haven::read_sav(
  file="E:\\医学统计学（第4版）\\各章例题SPSS数据文件\\例09-08.sav")
colnames(data9_8) <- c("number", "X", "Y")
# 默认method为pearson，如果有相同秩，会自动校正
1-sum((rank(data9_8$X)-rank(data9_8$Y))^2)*6/(nrow(data9_8)^3-nrow(data9_8))

## [1] 0.9050568

cor(data9_8$X, data9_8$Y, method="spearman")

## [1] 0.9050568

cor.test(data9_8$X, data9_8$Y, method="spearman")

## 
##  Spearman's rank correlation rho
## 
## data:  data9_8$X and data9_8$Y
## S = 92, p-value < 2.2e-16
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
##       rho 
## 0.9050568

# 模拟有相同秩的情况
a <- c(1, 2, 3.5, 3.5, 5, 6)
b <- c(2, 1, 3, 4, 5.5, 5.5)
1-sum((rank(a)-rank(b))^2)*6/(length(a)^3-length(a))

## [1] 0.9142857

cor(a, b, method="spearman")

## [1] 0.9117647

cor函数还有一个use参数来处理数据缺失的情况（NA)，默认为use="all.obs"，该情况下，如果数据有缺失，则报错，可以修改为use="complete.obs"，把含缺失数据的那一列删除后再运行，或者修改为use="pairwise.complete.obs"，把含缺失数据的那一行删除后再运行

参考：
https://www.statmethods.net/stats/correlations.html

第九章 双变量回归与相关

第九章 双变量回归与相关

知识清单

1. 直线回归

1.1 基本概念

1.2 计算方法

1.2.1 理论计算

1.2.2 R语言计算

1.3 统计推断

1.3.1 方差分析

公式

R语言实现

1.3.2 t检验

1.3.3 区间估计

2. 直线相关

2.1 相关概念

2.2 计算公式

2.3 统计推断

2.3.1 t检验

2.3.2 可信区间

2.4 决定系数

3. 直线回归应用注意事项

4. 秩相关

4.1 适用条件

4.2 Spearman秩相关

等级相关系数公式

统计推断

R语言实现

你可能感兴趣的:(第九章 双变量回归与相关)

第九章双变量回归与相关

第九章双变量回归与相关

你可能感兴趣的:(第九章双变量回归与相关)