CG中的仿射(affine transformation)和法线变换

Note

这是对MIT Foundation of 3D Computer Graphics第3章的翻译，本章讲解了仿射变换的基本概念，变换矩阵的由来以及分解、通用法线变换的推导等内容。本书内容仍在不断的学习中，因此本文内容会不断的改进。若有任何建议，请不吝赐教[email protected]

注：文章中相关内容归原作者所有，翻译内容仅供学习参考。
另：Github项目CGLearning中拥有相关翻译的完整资料、内容整理、课程项目实现。

---

已经完成的章节

• 第一章
• 第二章
• 第三章
• 第四章
• 第五章
• 第六章
• 第七章
• 第八章
• 第九章
• 第十章
• 第十一章
• 第十二章
• 第十三章
• 第十四章
• 第十五章
• 第十六章
• 第十七章
• 第十八章
• 第十九章
• 第二十章
• 第二十一章
• 第二十二章
• 第二十三章
• 附录B-仿射函数基础

---

仿射（并行）（Affine）

3.1 点和帧（Points and Frames）

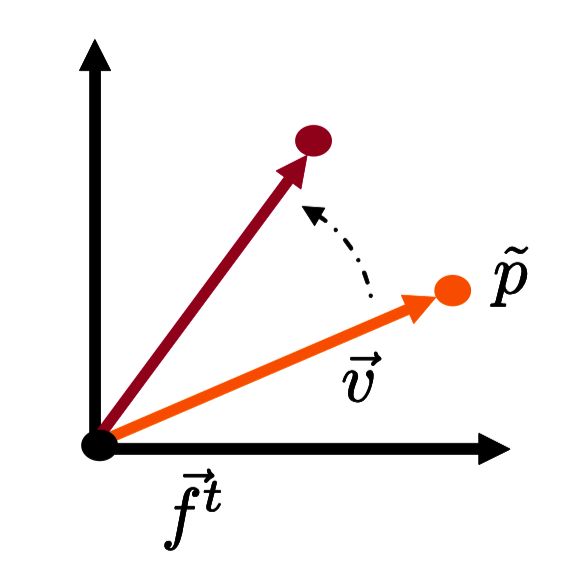
将点和矢量看作是两种不同的概念是有用的。点表示在几何世界中的某种固定位置，而矢量表示世界中两个点之间的运动。我们会使用两种不同的标记区分点和矢量。矢量会有一个箭头在顶部，而点会有波浪线在顶部。

如果我们认为矢量表达两点之间的运动，那么矢量操作（加法和标量乘法）就有明确的意义。如果我们把两个矢量加起来，我们在表达两个运动的串接（concatenation）。如果我们用一个标量乘以矢量，我们就在通过某个因子增加或减少运动。零矢量（zero vector）为一个特别矢量，其代表没有运动。

这些操作对于点不会真正产生任何意义。把两个点加起来应该表示什么含义，比如说，哈佛广场加上剑桥肯德尔广场（这里是两个地点名称）是什么？一个点被一个标量相乘又指得什么？什么是北极点的7倍？是否存在一个零点（zero point）和其它点的行为不一样？

存在一种在两个点之间确实有意义的操作：减法。当我们从另一个点减去一个点，我们应该会得到从第二个点到第一个点路径之间的运动，

反过来说，如果我们从一个点开始，然后移动一个矢量（位移），我们应该会到达另一个点。

对一个点应用线性变换同样有意义。例如我们可以想象一个点围绕某个固定原点的旋转。而且平移点也是有意义的（但是这个概念对于矢量没有任何意义）。要表达平移，我们需要开发仿射变换（或并行变换 affine transformation）的概念。要完成这个任务，我们借助矩阵。这些矩阵不仅对于处理本章的仿射（并行）变换很方便，而且对于描述（随后在第十章会看到的）相机投射变换也是很有帮助。

3.1.1 帧（Frames）

在仿射空间（affine space）中，我们描述任何点首先从某个原点开始，然后给其加上一个矢量的线性组合。这些矢量使用坐标和一个矢量基（basis of vectors）来表示。

此处被定义为。

而下面这行表达

被称为一个仿射帧（affine space）；它就像一个基（basis），但是由3个矢量和一个点组成。

为了借助一个帧指定一个点，我们使用拥有4个条目（entries）的4部件坐标矢量（coordinate 4-vector），其中最后一个条目总为1。要借助一个帧表达一个矢量，我们使用一个让0作为第4坐标的坐标矢量（也就是说，它只是基矢量之和）。当我们建模针孔相机的行为时，要表达几何形状（还有矩阵），4部件坐标矢量的使用都会很便利。

3.2 仿射变换和矩阵（Affine transformations and Four by Four Matrices）

相似于线性变换的情形，我们想要通过在一个4部件坐标矢量和一个帧之间放置一个合适的矩阵的形式，来定义出仿射变换的概念。

让我们将仿射矩阵定义为一个如下形式的矩阵

然后我们对一个点应用仿射变换如下

或者简写为

我们可以验证上面表达的第二行描述了一个有效的点，因为乘法

给出了我们一个带有1作为第4条目的4部件坐标矢量。另一方面，我们也能够看到乘法

此处被定义为，给出了一个由3个矢量和一个原点组成的有效帧。

同时也要注意到，如果矩阵的最后一行不是这种形式，变换就通常给出一个无效的结果。

类似于线性变换的情形，我们可以针对一个帧应用仿射变换（affine transformation）为

或者简写为

3.3 对点应用线性变换（Applying Linear Transformations to Points）

假如我们有一个表达线性变换的矩阵。我们可以将其嵌入矩阵的左上方角落，并且借助这个更大的矩阵对一个点（或者帧）应用变换。

这个变换在上拥有相同效果，就如之前其所参与的线性变换。如果我们把点当作从原点偏移矢量，我们就明白这个变换和应用线性变换到偏移矢量上具有相同效果。因而，以例子来说，如果矩阵为旋转矩阵，这个变换将围绕原点旋转这个点（参考图示）。正如下面我们将在第4章中看到的，当对一个点应用一个线性变换，帧的原点位置扮演了一个重要的角色。

我们借助下列缩写用于描述一个矩阵，其只是应用了一个线性变换。

此处是一个矩阵，是一个矩阵，右上角的0代表由0组成的矩阵，右下角的1是一个标量(scalar)。

Figure3.1.png

Figure 3.1: 对一个点应用线性变换。可以通过应用线性变换到始于原点的偏移矢量上来完成。

3.4 平移（Translations）

可以对点应用平移变换是很有用的。这种变换不是线性的（参考课后练习6)。仿射变换的主要新威力就是在线性变换之上表达平移的能力。实际上，如果我们应用变换

我们看到变换在坐标上的效果为

针对平移，我们使用简写

此处为 一个矩阵，为一个同一矩阵（identity matrix），右上角的为一个表达平移的矩阵，左下角的0表示一个由0组成的矩阵，右下角的1为一个变量。

注意如果在第4坐标中为0，如此就表达了一个矢量而不是一个点，从而不会被平移所影响。

3.5 汇总（Putting Them Together）

任何仿射矩阵（affine matrix）都可以被分解为线性部分和平移部分。

或者简写为

注意因为矩阵乘法不是可互换顺序的，乘法中的顺序很关键。一个仿射矩阵（affine matrix）也可以借助一个不同的平移矩阵被分解为（线性部分是不会发生变化的），但是我们不会使用这种形式。

如果，的线性部分，是一个旋转，我们把这种形式记作

在这种情形中，我们称矩阵为刚体矩阵(rigid body matrix)，它所对应的变化，刚体变换（rigid body transform），简称。刚体变换保留了矢量之间的点积（dot product），基的手（螺旋）性（handedness），还有点之间的距离。

3.6 法线（Normals）

在计算机图形学中，我们经常借助表面法线确定一个表面点如何被着色。所以当表面点经历由矩阵表示的仿射变换时，我们需要懂得表面法线是如何变换的。

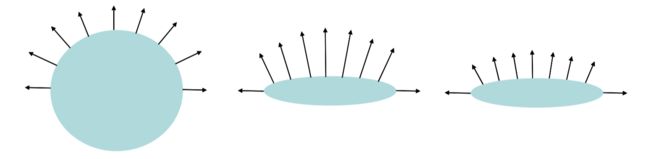
你可能猜测我们只要用矩阵乘以法线的坐标就可以了。例如，如果我们旋转几何形状，法线会以完全相同的方式旋转。但是事实上使用矩阵不总是正确的。例如在图示中，我们顺着轴挤压一个球体。在这种情形中，实际的法线变换会顺着轴拉伸而不是挤压。在这里我们要推导出可以应用在所有情形中的正确变换。

Figure3.2.png

Figure 3.2: 左侧：蓝色的形状拥有以黑色表示的法线。中间：现在在轴方向上被缩小同时（未标准化的）法线在轴方向被拉伸。右侧：法线被重新标准化从而给出被挤压形状的正确的单位法线。

让我们定义位于点上平滑表面的法线为一个矢量，这个矢量正交于那个点表面的切线平面。切线平面是矢量平面，这个矢量平面通过临近的（距离无限小地）表面点之间的减法来定义，所以，针对法线和两个非常接近的点和，我们有如下表达。

在某种固定的正交标准化坐标系中，这可以被表达为

在这个公式中我们在前面的插槽中使用是因为它被0乘，从而和结果不相关。

假设存在一个由仿射矩阵表示的仿射变换，我们把这个变换应用到所有的点上。什么矢量会和任意的切线矢量保持正交状态？让我们重写方程式(3.4)为

如果我们定义为被变换点的坐标，同时让，那么我们就得到如下表达

并且我们看到是被变换的几何体法线的坐标（要依靠伸缩变换来获得标准态）。

注意因为我们不关注值，因而我们不需要关注的第四列。同时，因为A是一个仿射矩阵（affine matrix），所以也是，进而剩下三列的第四行全部是0，从而可以安全地被忽略。因而，参考简写方式

我们可以得到这种关系

此时调换整个表达式，我们就获得最终表达式

此处是矩阵的反转加调换（等价于调换加反转）。注意如果为一个旋转矩阵，且这个矩阵是正交标准化的，那么它的反转加调换事实上仍然是。在这种情形中法线的坐标表现的就像点的坐标一样。然而对于其它线性变换，法线的表现就不相同了。（参考图示。）同时也要注意到A的平移部分对法线没有影响。