下面正题开始。
一般性的,都能想到 dummy head 的技巧以及Java中LinkedList(底层是双向(循环)链表)。
Leetcode 返回一个头结点对象,就算返回整个链表了,而我们自己实现一般会 new 一个链表对象实例,然后调用该实例的各类方法来操作整个链表。
1|0单链表
1|1基本认识
之前写的动态数组并非真正动态,因为其内部封装的是一个容量不可变的静态数组。
而这里的链表则是真正的动态数据结构(不需要处理固定容量问题,即增删效率高,但由于不知道实际地址/索引,所以也丧失了随机访能力)。
辅助其他数据结构:二分搜索树,AVL/红黑树,它们基于链表实现。
基本构成: 节点 + 指针。
class Node {
E e;
Node next;
}
最后一个节点一般指向 null
为了方便或者统一操作,一般会有 Node head,头结点。
头结点的存在一般是为了在头部操作 (就像动态数组的新元素索引始终是 size 位置)
一般直接用头结点指向首个节点(第一个节点即 head,但它不存储元素) dummy head
之所以用 dummy head 的原因,其实是为了操作简便。(不用也可以,但实现上的写法就...)
打个比方,你要删除/增加某个节点时,一般情况而言,一定要知道删除节点的前一个节点(在头部则没有必要);一般都是通过循环遍历往后先找到特定节点,但是如果没有 dummy head,那么就要区分是在头结点还是中间节点操作(在脑海中想一下就知道了)。
有了 dummy head,头结点前面也有节点了,所以整个操作行为是统一的,一致的,不需要再做情况区分。
(下面有案例)
1|2实现框架
先把实现的框架列一下,大致如下:
package linkedlist;
public class LinkedList {
//定义一个内部类,作为节点类
private class Node {
public E e;
public Node next; //便于 LinkedList 访问
public Node(E e, Node next) {
this.e = e;
this.next = next;
}
public Node(E e){
this(e, null);
}
public Node(){
this(null, null);
}
@Override
public String toString() {
return e.toString();
}
}
//操作链表的辅助变量
private int size;
private Node head; //头结点
//构造函数
public LinkedList() {
head = null;
size = 0;
}
public int getSize() {
return size;
}
public boolean isEmpty() {
return size == 0;
}
}
然后再来实现其中的增删改查,此时先不设置虚拟头节点。
1|3添加操作
这里实现的头部添加 (后续再扩展其他添加):
public void addFirst(E e) {
/*
Node node = new Node(e);
node.next = head;
head = node;
*/
//简写
head = new Node(e, head);
//维护链表长度
size++;
}
在某个位置插入元素:
情况1: 链表中间的节点,先找到相应位置前一个节点,然后创建新节点,插入
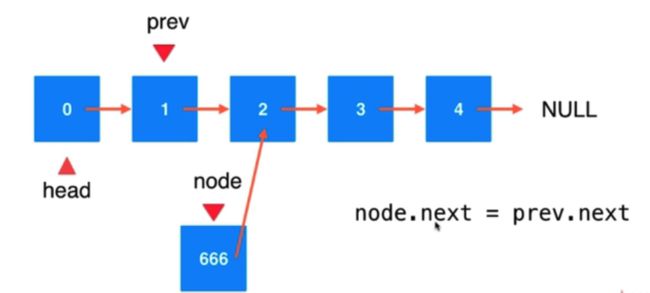
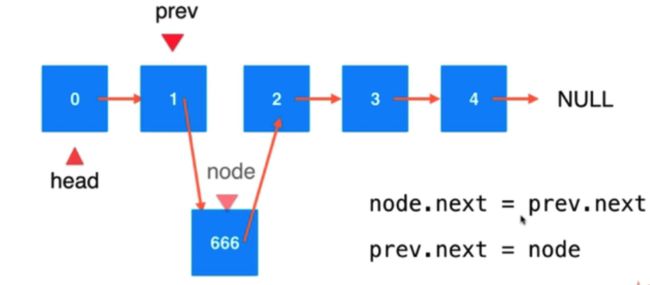
情况2: 如果是第一个节点,那么是不存在前一个节点的。直接用 addFirst 的方式
//指定的 index 位置添加元素 (先要找到 index 前一个位置)
// index 从 0 ~ size-1
public void add(int index, E e) {
// 索引有问题
if (index < 0 || index > size) { //当 index == size 时,表示在末尾添加
throw new IllegalArgumentException("Add Failed, Illegal index");
}
if (index == 0) {
addFirst(e);
} else {
Node prev = head;
//找到指定位置前一个节点
for (int i = 0; i < index - 1; i++) {
prev = prev.next;
}
//创建一个新节点
/*Node node = new Node(e);
node.next = prev.next;
prev.next = node;*/
//简写
prev = new Node(e, prev.next);
size++;
}
}
(可以看到上面确实是区分不同的情况了的)
此时在末尾添加元素,即 index = size 的位置添加,直接调用 addLast 即可:
//在末尾添加元素
public void addLast(E e){
add(size, e);
}
1|4头结点优化
不着急往后探索,这里先把头节点优化一下,即加入 dummy head,统一整个操作流程。
上面的操作 add ,由于链表头结点 head 并没有前面一个节点,所以插入的时候确实要特殊一些。(如果第一个节点之前有节点,那么整个操作就统一了)
优化方法,在头结点前面添加一个 虚拟节点,即不存储任意元素的节点。
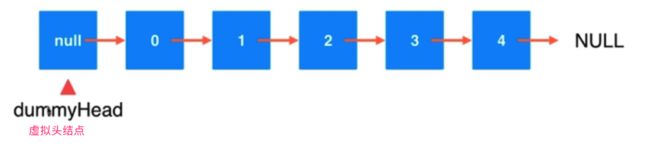
内部机制,用户(client) 不知道虚拟节点的存在。(只是为了方便逻辑操作)。
相关修改:
构造函数需要修改,初始化 LinkedList 的时候就要创建一个节点
public LinkedList1() {
dummyHead = new Node(null, null);
size = 0;
}
添加元素可以统一用 add,然后让 addFirst 和 addLast 调用 add 方法即可。
//指定的 index 位置添加元素 (先要找到 index 前一个位置)
// index 从 0 ~ size-1
public void add(int index, E e) {
// 索引有问题
if (index < 0 || index > size) { //当 index == size 时,表示在末尾添加
throw new IllegalArgumentException("Add Failed, Illegal index");
}
//因为在实际 index 取值范围内,总能找到相关节点的前一个节点
Node prev = dummyHead;
//找 index 之前的节点
for(int i = 0; i < index; i++){
prev = prev.next;
}
prev = new Node(e, prev.next);
size++;
}
//头部插入
public void addFirst(E e) {
add(0, e);
}
//在末尾添加元素
public void addLast(E e){
add(size, e);
}
虚拟头结点的引入,方便了其他许多链表的操作(只要涉及类似的遍历查找)。
1|5获取操作
//获取某元素
public E get(int index) {
//先检查索引的合法性
if(index<0 || index > size-1) {
throw new IllegalArgumentException("Get Failed, Illegal index");
}
// 和前面找 index 节点前一个节点不同(那里是从第一个节点前面的虚拟节点开始)
// 这里就要找 index 节点,索引从 dummyHead.next 开始,即真正的第一个节点开始
Node ret = dummyHead.next;
for(int i =0; i < index; i++) {
ret = ret.next;
}
return ret.e;
}
获取第一个元素,最后一个:
//获取第一个
public E getFirst() {
return get(0);
}
//获取最后一个
public E getLast() {
return get(size -1);
}
1|6修改元素
把 index 位置的元素修改为 E。
(找到节点,然后替换里面的元素 e)
public void set(int index, E e) {
//先检查索引的合法性
if (index < 0 || index > size - 1) {
throw new IllegalArgumentException("Get Failed, Illegal index");
}
//找到节点,然后替换里面的元素
Node curr = dummyHead.next;
for (int i = 0; i < index; i++) {
curr = curr.next;
}
curr.e = e;
}
1|7查找元素
一直遍历到元素末尾,然后寻找尾巴。
//查找元素
public boolean contains(E e) {
Boolean ret = false;
//在 size 范围内遍历查找
Node curr = dummyHead.next;
/*for(int i=0; i
if(curr.e.equals(e)){
ret = true;
break;
}
curr = curr.next;
}*/
//其实可以用 while 循环 (多判断一次 size 位置)
while(curr != null) {
//当前节点是有效节点
if(curr.e.equals(e)){
ret = true;
break;
}
curr = curr.next;
}
return ret;
}
1|8遍历打印
多种循环的写法:
//打印方法
@Override
public String toString() {
StringBuilder res = new StringBuilder();
//从头遍历到尾巴
/*Node curr = dummyHead.next;
while(curr != null) {
res.append(curr + "->");
curr = curr.next;
}*/
//简写
for(Node curr = dummyHead.next; curr != null; curr = curr.next) {
res.append(curr + "->");
}
res.append("null");
return res.toString();
}
简单测试一下:
//测试元素
public static void main(String[] args) {
LinkedList1 linkedlist = new LinkedList1<>();
//放入元素 0, 1, 2, 3, 4
for(int i =0; i < 5; i++) {
linkedlist.addFirst(i); //O(1)
System.out.println(linkedlist);
}
System.out.println(linkedlist);
//尝试插入一个元素
linkedlist.add(1, 100); // 4, 100, 2, 3, 1, 0, null
System.out.println(linkedlist);
}
打印结果:
0->null
1->0->null
2->1->0->null
3->2->1->0->null
4->3->2->1->0->null
4->3->2->1->0->null
4->100->3->2->1->0->null
1|9删除元素
还是要 先找到前一个节点 。(也就是说还是借助虚拟头结点)
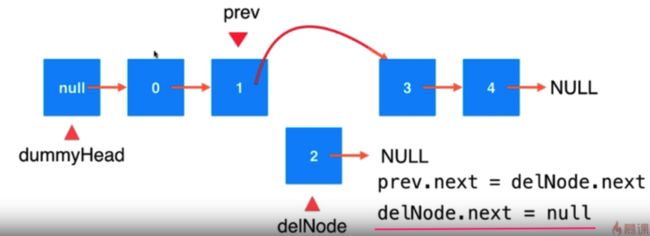
简单一句话,然 delNode 和原来的链表脱离。(delNode 置空非必须)
编码实现:
//删除元素
public E remove(int index){
if (index < 0 || index > size - 1) {
throw new IllegalArgumentException("Delete Failed, Illegal index");
}
//找到相关节点的前一个节点
Node curr = dummyHead;
for(int i = 0; i < index; i++) {
curr = curr.next;
}
Node delNode = curr.next;
//删除
curr.next = delNode.next;
delNode.next = null;
//必须维护 size
size--;
return delNode.e;
}
//删除第一个节点
public E removeFirst() {
return remove(0);
}
//删除最后一个节点
public E removeLast() {
return remove(size-1);
}
//删除指定元素
public void removeElem(E e) {
//从 dummyHead 开始找,找到就删除,否则就不删除
Node curr = dummyHead;
boolean found = false;
while (curr.next != null) {
if (curr.next.e.equals(e)) {
found = true;
//删除操作
Node delNode = curr.next;
curr.next = delNode.next;
delNode.next = null;
size--;
break;
}
curr = curr.next;
}
if (!found) {
throw new RuntimeException("要删除的元素不存在");
}
}
测试一下:
//测试元素
public static void main(String[] args) {
LinkedList1 linkedlist = new LinkedList1<>();
//放入元素 0, 1, 2, 3, 4
for(int i =0; i < 5; i++) {
linkedlist.addFirst(i); //O(1)
System.out.println(linkedlist);
}
System.out.println(linkedlist);
//尝试插入一个元素
linkedlist.add(1, 100); // 4, 100, 2, 3, 1, 0, null
System.out.println(linkedlist);
//尝试删除 index = 1 位置的 100
linkedlist.remove(1);
System.out.println(linkedlist); //4->3->2->1->0->null
//删除最后一个元素 0
linkedlist.removeLast();
System.out.println(linkedlist); //4->3->2->1->null
//删除第一个元素
linkedlist.removeFirst();
System.out.println(linkedlist); //3->2->1->null
//删除指定元素
linkedlist.removeElem(3);
linkedlist.removeElem(1);
//linkedlist.removeElem(null);
System.out.println(linkedlist);
}
1|10时间复杂度
链表虽然不移动元素,但是涉及到从前往后找到(检查)相应的位置/元素。
添加操作:
addFirst(), O(1) 因为采用的是头插法
addLast(), O(n) 涉及循环遍历到尾部,然后插入
add(), O(n) 其实是 O(n/2) 即 O(n)
删除操作:
同上。
修改操作: O(n)。
查找操作:
get(), contains(), find() 一律 O(n),因为并不支持随机访问呀。
2|0单链表应用
2|1链栈
上面也说了,如果只在链表头增删时,它的整体复杂度是 O(1),这不正好用于栈么?
简单记忆一下,同侧操作
栈的底层实现是链表,而不是动态数组了
package stack;
import linkedlist.LinkedList1; //这是有 dummy head优化的链表实现
public class LinkedListStack implements Stack{
//链栈内部实际采用链表存储
private LinkedList1 list;
public LinkedListStack(){
list = new LinkedList1<>();
}
@Override
public boolean isEmpty() {
return list.isEmpty();
}
@Override
public int getSize() {
return list.getSize();
}
@Override
public E pop() {
return list.removeFirst();
}
@Override
public E peek() {
return list.getFirst();
}
@Override
public void push(E e) {
list.addFirst(e);
}
@Override
public String toString() {
StringBuilder res = new StringBuilder();
res.append("Stack: top [");
res.append(list);
res.append("]");
return res.toString();
}
public static void main(String[] args) {
LinkedListStack stack = new LinkedListStack<>();
//放入元素 0, 1, 2, 3, 4
for(int i =0; i < 5; i++) {
stack.push(i); //O(1)
System.out.println(stack);
}
System.out.println(stack);
System.out.println(stack.peek());
//弹出一个元素
stack.pop();
System.out.println(stack);
}
}
测试结果:
Stack: top [0->null]
Stack: top [1->0->null]
Stack: top [2->1->0->null]
Stack: top [3->2->1->0->null]
Stack: top [4->3->2->1->0->null]
Stack: top [4->3->2->1->0->null]
4
Stack: top [3->2->1->0->null]
和数组实现的栈的不同,数组是在尾巴上插入,可能涉及动态扩容,均摊复杂度是 O(1),而链栈始终就是O(1)。
但是 linkedlist 的 new 操作时非常耗时的 (特别是大量对象创建)
真实运行结果是不确定的 (ArrayStack VS LinkedListStack),因为数量级一致
2|2链队列
因为队列涉及头和尾的操作,所以如果用链表,那一般要添加一个尾指针。
因为 head 和 tail 都是指针,所以入队和出队相当于改变指向那么简单,但谁做头谁做尾巴?(相当于 head, tail 指针往哪个方向移动)
如果要删除 tail 元素并不容易(无法做到O(1)),因为删除元素要知道 tail 前面一个元素。但是 tail 增加,则可以直接添加。(head不用管, 它的增删都比较容易)
所以结论显而易见:
tail 用作队尾 (即用于增加元素, tail 指针右移)
head 用作队首 (删除元素,出队)
此时还需要 dummy head 么,分析上面的 tail, head,显然不需要操作统一了,所以不需要哑结点。
这里就不复用 LinkedList 了,而是专门再在内部实现链式存储。(Node 内部类还是需要的)
特别注意:
链表为空的情况
只有一个元素的情况,此时即便是出队,也要 head = tail = null;
//内部采用链式存储的队列
public class LinkedQueue implements Queue {
//定义一个内部类,作为节点类
private class Node {
public E e;
public Node next; //便于 LinkedList 访问
public Node(E e, Node next) {
this.e = e;
this.next = next;
}
public Node(E e) {
this(e, null);
}
public Node() {
this(null, null);
}
@Override
public String toString() {
return e.toString();
}
}
private Node head, tail;
private int size;
//构造器
public LinkedQueue() {
head = tail = null;
size = 0;
}
@Override
public boolean isEmpty() {
return size == 0;
}
@Override
public int getSize() {
return size;
}
@Override
public E dequeue() {
//出队操作,在队首
//没有元素肯定就不能出队
if (isEmpty()) {
//或者 head = null
throw new IllegalArgumentException("Cannot dequeue from an empty queue");
}
//正常出队,提取 head
Node retNode = head; //tail,考虑只有一个元素的队列
head = retNode.next;
retNode.next = null;//游离对象
//仅在只有一个元素的队列,需要维护 tail
if (head == null) {
tail = null;
}
size--;
return retNode.e;
}
@Override
public E getFront() {
if (isEmpty()) {
//或者 head = null
throw new IllegalArgumentException("Cannot dequeue from an empty queue");
}
return head.e; // 返回队首即可
}
@Override
public void enqueue(E e) {
//入队操作,在尾部操作
if (tail == null) { //说明此时队列是空的,即 tail 和 head 都为空
tail = new Node(e);
head = tail;
} else {
tail.next = new Node(e);
tail = tail.next;
}
size++;
}
@Override
public String toString() {
StringBuilder res = new StringBuilder();
res.append("Queue: front[ ");
for(Node curr = head; curr != null; curr = curr.next){
res.append(curr.e + "->");
}
res.append("null ] tail");
return res.toString();
}
public static void main(String[] args) {
LinkedQueue queue = new LinkedQueue<>();
//存储 11 个元素看看
for(int i=0; i<11; i++){
queue.enqueue(i);
System.out.println(queue); // 在 10 个元素满的时候回扩容
}
//出队试试
System.out.println("------出队");
queue.dequeue();
System.out.println(queue);
郑州人流医院哪家好:http://www.zzchxb120.com/
运行结果如下:
Queue: front[ 0->null ] tail
Queue: front[ 0->1->null ] tail
Queue: front[ 0->1->2->null ] tail
Queue: front[ 0->1->2->3->null ] tail
Queue: front[ 0->1->2->3->4->null ] tail
Queue: front[ 0->1->2->3->4->5->null ] tail
Queue: front[ 0->1->2->3->4->5->6->null ] tail
Queue: front[ 0->1->2->3->4->5->6->7->null ] tail
Queue: front[ 0->1->2->3->4->5->6->7->8->null ] tail
Queue: front[ 0->1->2->3->4->5->6->7->8->9->null ] tail
Queue: front[ 0->1->2->3->4->5->6->7->8->9->10->null ] tail
------出队
Queue: front[ 1->2->3->4->5->6->7->8->9->10->null ] tail
到这里,单链表基本探究完毕了。
3|0其他链表
下面说的这些链表其实也很常用,但是个人要去实现的话,就费事儿啊
(除非你是大学教师,或者学生,或者自由作家,有的是时间耐得住寂寞,磨啊)
3|1双向链表
这个维护代价其实有点大,有点就是节点之间的联系更加方便了。(单链表时也会维护尾指针)
比如尾端删除,不用从头开始找尾端前一个元素了,避免了 O(n) 复杂度