AC自动机中,转移的最小单位是一个字符。也就是说,匹配后只能移动一个字符,复杂度是线性的O(n)
。然而线性并非最快,Boyer-Moore算法在匹配后可以跳过多个字符,比线性还快。据说在实践中,利用Boyer-Moore优化的AC自动机总是更快。
来熟悉一下Boyer-Moore算法的基本思路。假设模式串的长度为m
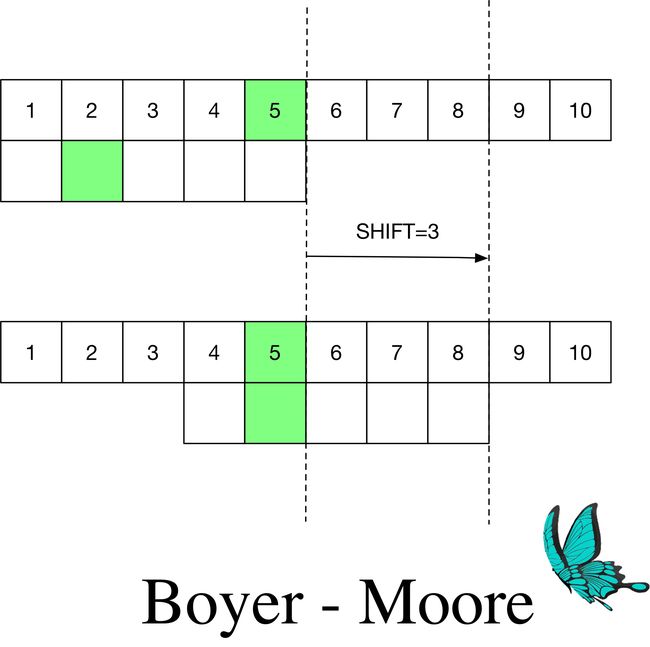
,母文本为t。算法不是去母文本中找模式串,而是在模式串中从右到左找文本的第 m个字符tm。如果没找到,那么就可以在母文本中跳过m个字符,继续搜索t2m。如果找到了,比如说是模式串的第2个字符,那就可以跳过m−2个字符,继续搜索t2m−2,以此类推。ti恰好与模式串尾部匹配的时候,再比较剩下的ti−1⋯tt−m,直到这m个字符都匹配上。该算法可利用下图演示(二进制串匹配,白色代表0,绿色代表1
):
上例在匹配下标5
后直接快进了3
个字符。
Wu Manber利用了Boyer-Moore的思路,将该算法拓展到多模式匹配。
预处理
第一步要算出所有模式串上的最小长度m
,然后先考虑每个模式串的前m个字符。如此所有模式串长度都一样了。注意如果最短模式串非常短,比如长度为1,则算法不可能跳过2
及以上个字符,效率变低。
如果每次比较不局限于1
个字符,而是比较B个字符,则比较次数可以减小到1B。同时每次在模式串位置i匹配上了之后可以跳过的字符数减小到m−i−B+1,都不匹配时i=0
。
SHIFT表的构造
用一个SHIFT表储存匹配后最大可以跳过的字符数,将每个长B
的“子串”哈希到一个整数,对应SHIFT表中的下标。那么SHIFT表的大小理论上是∥Σ∥B,其中Σ
是字符表。
SHIFT表还可以理解为,后缀作为子串在模式串中离尾部的最短距离(上图为3
)。
记正在扫描的B
个字符为X=x1⋯xB,并且X被哈希到i,在所有模式串从右到左寻找X
,则会发生两种情况:
所有模式串都不含X
此时可以跳过m−B+1
,将其存入SHIFT[i]中。
存在包含X
的模式串
找到X
在这些模式串中的下标中的最大值(也即最右位置)
q,将
m−q存入SHIFT[i]。
为了得到这样的SHIFT表,只需枚举所有模式串(的前m
个字符)中长
B的子串
aj−B+1⋯aj,将
m−B+1(子串位于模式串首部之外,即不含该子串)和
m−j(子串位于模式串的下标
j处)中的较小者存入SHIFT表即可。这个值代表最少需要移动多少个字符来“对齐”这个子串,大于这个值的话会遗漏某些模式串,小于等于这个值则是安全的。
SHIFT表的压缩
考虑到SHIFT表可能很大,现在看看如何压缩。SHIFT表的定义是匹配子串时最大可以跳过的字符数,如果这个值比精确值大,算法会出错;然而小一点则不会出错,只会降低效率。于是可以将一些子串放到同一个下标中,只需将SHIFT值设为它们的SHIFT值的最小值。实践中在模式串很少的时候,使用B=2
、精确形式;在模式串很多的时候使用
B=3、压缩形式。
HASH表的构造
在SHIFT[h]=0
的时候(尾部
B个字符匹配成功,不应该跳过,也就是说匹配到了公共后缀)需要找到那些以该子串结尾的模式串,复用SHIFT表的哈希函数,制作另一张HASH表,值为以该子串结尾的所有模式串。HASH表比SHIFT表稀疏(因为只储存后缀),可以考虑只利用哈希值最后几个比特得到更紧凑的结构。
记h
为哈希函数的输出值,将所有模式串按后缀的哈希排序,那么必然有一些连续区域的哈希值是相同的,也就是说这些区域共享长
B的后缀。将排序后的模式串记录为链表,其中的指针记为
p。那么HASH表格就是以索引连续区域(子链表)为目标构造的结构。
SHIFT[h]=0
时,此时
HASH[h]指向一个子链表的首部
p,不断递增
p直到
p+1等于
HASH[h+1]时即可得到子链表的尾部元素。
PREFIX表的构造
由于自然语言中的单词经常共享后缀,比如ion或ing。这会导致HASH表中索引的模式串分布非常不均匀,产生大量冲突。极端情况下可能所有模式串都被映射到同一条目中。此时必须对所有模式串逐一比对,降低了效率。为了解决这个问题,引入了另一个PREFIX表。
在上一节中HASH表维护的是长B
的后缀,类似地PREFIX维护的长
B′的前缀。HASH表除了索引模式串本身外,还索引了模式串长
B′的前缀的哈希值。在母文本与模式串的后缀匹配的情况下,先用HASH表得到所有后缀相同的模式串,然后用母文本长
m的窗口移动
m−B′得到前缀,去PREFIX表得到哈希值,用这个哈希值过滤一下,剩下的就是需要逐一匹配的模式串。
事实上PREFIX表不是算法必须的,特别是在一些公共后缀不多的情况下。PREFIX表其实也不是一张Key-Value表,只是一个哈希函数而已,记作PREFIX(x)。
匹配
其实匹配的过程在预处理环节已经提到不少,正是因为匹配时要用到,所以才需要这3个表格的预处理。归纳起来,匹配过程的主循环可以描述为如下4步:
计算母文本中当前长B
。
检查SHIFT[h]:如果>0
则跳过SHIFT[h]个字符并转到1;否则,转到3。
计算当前位置往左m
的长
B′的前缀的哈希值,记为text_prefix_hash
检查HASH[h]≤p<HASH[h+1]
区间内的p是否有PREFIX(p)=text_prefix_hash,当两者相等时,进一步直接比较模式串与这段来自母文本的子串。当它们完全匹配的时候,就找到了一个模式串。无论找到与否,都将当前位置右移1个字符,并跳转1。
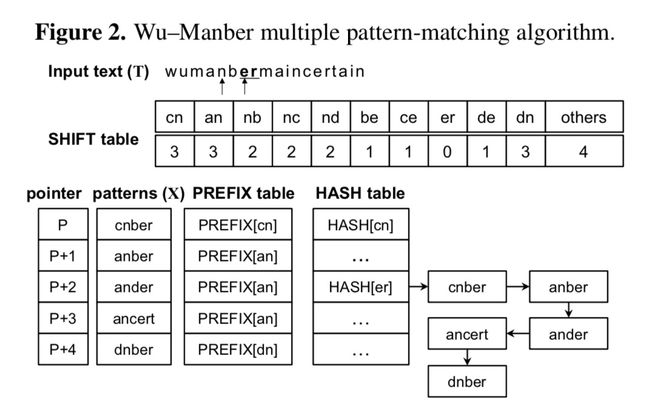
Oh et al. (2014)举了个例子:
这里m=5,B=B′=2
,当前正在匹配的后缀是nb,前缀是um。由于在所有模式串中,nb离尾部的距离最小为
2,所以SHIFT[nb]=
2,跳过
2个字符;此时后缀变为er,前缀变为an。后缀er的SHIFT值为0,检查一下HASH表中具有公共前缀的模式串{anber, ander, ancert},发现anber完全匹配。输出anber后,当前位置移动
1个字符,跳转
1。
事实上,在后缀匹配成功后,总是只能跳1
个单位,依然不够快。另外,HASH表已经够费内存的了,额外再加一个PREFIX表,双倍内存。
复杂度
P
个模式串,
M=mP是所有模式串的总长度,最多
P=M/m个子串对应同一个
SHIFT值i (极端情况下所有模式串在位置i 的子串都相等)。长B 的子串最少有M 个(极端情况下B=1 ,所有模式串长度都为1 。这是我的理解,与论文给出的2M 不同,我举出的反例如上所述)。所以随机挑一个子串,它的SHIFT值为某个特定值i 的概率小于两者之比1/m。
哈希函数的复杂度是O(B)
,母文本长度N ,不跳转的情况下(i=0 )复杂度为三者乘积O(BN/m) ;跳转的情况下,平均SHIFT值为1+⋯+m−B+1m=O(m2) ,复杂度为哈希复杂度乘以文本长度除以平均SHIFT值,也是O(BN/m) 。所以Wu Manber是总体复杂度就是O(BN/m)。
变种
为了解决SHIFT[i]=0
时无法跳过更多字符的问题,
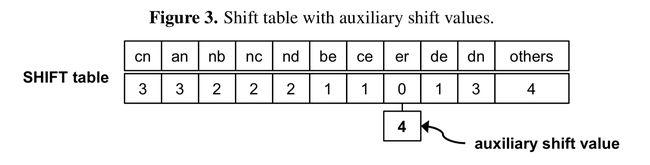
Oh et al. (2014)提出对所有这样的后缀额外记录一个SHIFT值,代表该后缀第2小的SHIFT值,称为auxiliary shift(ASHIFT)。匹配成功后按ASHIFT快进。
为什么可以跳过这么多呢?因为SHIFT[i]
的定义保证了所有模式串在跳过的区间内不会含有该后缀i 。当SHIFT[i]=0 时,最短距离为0 已经考虑了,接着跳过所有模式串中i离尾部的第二短距离,当然是安全的。
ASHIFT表的构造
在构造SHIFT表的过程中,当新的SHIFT[i]=0
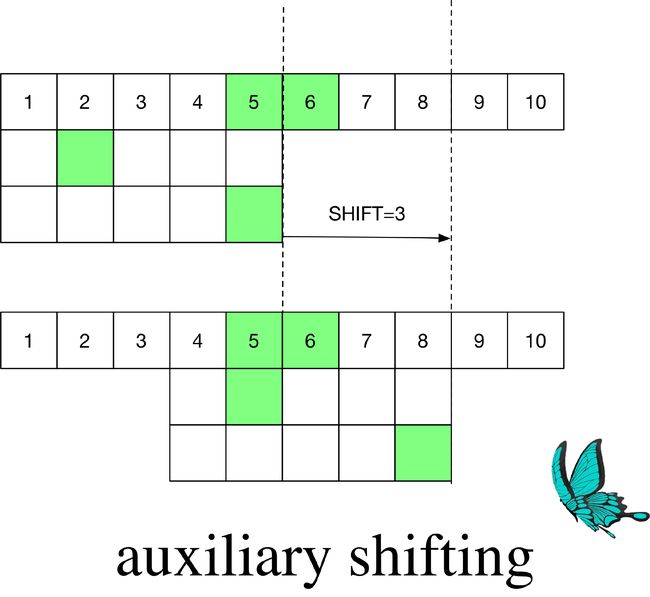
时,如果ASHIFT[i]≠NULL ,用旧的SHIFT[i] 和ASHIFT[i] 中的较小者更新ASHIFT[i] 。如果说SHIFT[i] 储存的是后缀作为模式串的子串离尾部的最短距离的话,ASHIFT[i]储存的就是第二短的距离。这个过程可以用下面两张图描述:
m=5,B=1
,一共两个模式串。
此时第二短的距离是3
,来自第一个模式串。
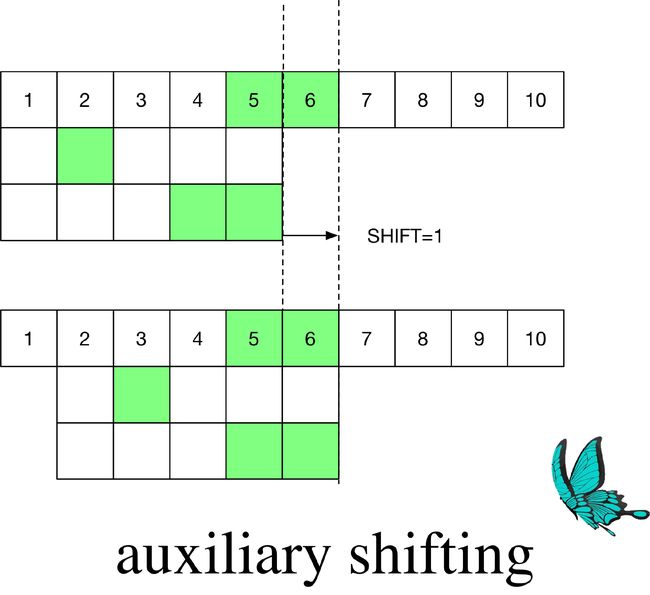
此时第二短的距离是1
,来自第二个模式串(最短距离来自相同的模式串)。
回过头来看对上一个例子的加速,由于所有模式串的前5
个字符都以
er结尾,所以
ASHIFT[er]=m−B+1=4:
在匹配了er之后不再只跳过1
,而是可以安全地跳过
4个字符:
Early Decision Method
在步骤4检查HASH[h]≤p<HASH[h+1]
区间内的p是否有PREFIX(p)=text_prefix_hash时,可以通过预先排序PREFIX(p)。检索有序列表比无序列表快。即使后缀和前缀都匹配上了,剩下的片段也可以预先排序。有序列表上的顺序检索可以early stopping。
总结
Wu Manber算法理论上复杂度为O(BN/m)
(1≤B≤m=min(strlen(M)) ),与AC自动机的O(N) 相比,只有在特定条件下(B≪m )才能体现出优势。这个特定条件很苛刻,要求模式串不能太短。而在自然语言处理的场景下,经常有单字作为模式串的情况,此时Wu Manber无法跳过多个字符,没有优势。另外,汉语最常见的词语长度为2,也限制了该算法的使用。
另一方面,Wu Manber所依赖的哈希表则带来了很大的内存负担,如果哈希函数复杂度本身很高,更加得不偿失。
题外话,算法研究没有止境,再简单的问题,也有一条历史悠久的进化路线与错综复杂的变种。