图
图(Graph)是由顶点和连接顶点的边构成的离散结构。在计算机科学中,图是最灵活的数据结构之一,很多问题都可以使用图模型进行建模求解。图的结构很简单,就是由顶点集和边集构成,因此图可以表示成G=(V,E)。 它也分为无向图、有向图、加权图。
在使用图地过程中经常会用到队列、优先队列、栈等的辅助。所以本例中除了图相关的定义外,还定义了队列和优先队列。
定义队列类
class Queue():
# 定义队列类,先进先出
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def enqueue(self, item):
self.items.insert(0, item)
def size(self):
return len(self.items)
def dequeue(self):
return self.items.pop()定义图中的顶点
class Vertex:
# 包含了顶点信息,以及顶点连接边信息
def __init__(self, key):
self.id = key
self.connectedTo = {}
self.distance = 0 # 距离
self.previous = None # 标记前一个顶点
self.color = 'white'
self.disc = 0 # 标记discoveryTime
self.fin = 0 # 标记finishTime
def getId(self):
return self.id
def addNeighbor(self, nbrKey, weight):
self.connectedTo[nbrKey] = weight
def getConnections(self):
return self.connectedTo.keys()
def __str__(self):
return str(self.id) + ' connectedTo: ' + str([x.id for x in self.connectedTo])
def getWeight(self, nbrkey):
return self.connectedTo[nbrkey]
def setColor(self,color):
self.color = color
def getColor(self):
return self.color
def setDistance(self, distance):
self.distance = distance
def getDistance(self):
return self.distance
def setPred(self,preVertex):
self.previous = preVertex
def getPred(self):
return self.previous
def setDiscovery(self,dtime):
self.disc = dtime
def getDiscovery(self):
return self.disc
def setFinish(self,ftime):
self.fin = ftime
def getFinish(self):
return self.fin定义图
class Graph:
# 包含了各顶点和连接边的图
def __init__(self):
self.vertList = {}
self.numVertices = 0
def addVertex(self, key):
self.numVertices += 1
newVertex = Vertex(key)
self.vertList[key] = newVertex
return newVertex
def getVertex(self, key):
if key in self.vertList:
return self.vertList[key]
else:
return None
def __contains__(self, key):
return key in self.vertList
def addEdge(self, fromKey, toKey, cost=0):
if fromKey not in self.vertList:
nv = self.addVertex(fromKey)
if toKey not in self.vertList:
nv = self.addVertex(toKey)
self.vertList[fromKey].addNeighbor(self.vertList[toKey],cost)
def getVertices(self):
return self.vertList.keys()
def __iter__(self):
return iter(self.vertList.values())图的应用举例1--词梯
WordLetter 方法1: 首先将所有单词作为顶点加入图中,再高潮建立顶点之间的边; 它的时间复杂度为O(n^2),n为单词个数。
方法2: 创建多个桶,每个桶可以存储多个单词,桶使用通配符""作为标记,""占空一个字母,所以匹配标记的单词都放到同一个桶中;然后再对同一个桶中的单词之间建立边。
def buildWordGraph(wordFile):
d = {}
g = Graph()
wfile = open(wordFile,'r')
for line in wfile:
word = line[:-1]
for i in range(len(word)):
#每个单词产生四种bucket,判断字典中是否存在该桶,如果存在则该桶直接追加单词,如果不存在则创建该桶,并存放单词
bucket = word[:i] + '_' + word[i+1:]
if bucket in d:
d[bucket].append(word)
else:
d[bucket] = [word]
#为每个桶中的不同单词建立边
for bucket in d.keys():
for word1 in d[bucket]:
for word2 in d[bucket]:
if word1 != word2 :
g.addEdge(word1, word2)
return g广度优先搜索算法Breadth First Search(BFS)
给定图G 及开始搜索的起始顶点s: BFS搜索所有从s可到达目标顶点的边;在达到更远距离k+1的顶点之前,BFS会找到全部距离为k的顶点;
可以把s想象成为树根,构建一棵树的过程,从顶点向下逐步增加层次,BFS可以保证在增加距离(层次)之前,添加了所有兄弟节点到树中。从队首取出一个顶点作为当前顶点(出队);遍历从当前顶点到邻接顶点,如果是白色,则将其改为灰色,距离加1,其前驱顶点为当前顶点,将其加入到队列中; 遍历完成后,将当前顶点设置为黑色,循环回到步骤1的队首取当前顶点。
def bfs(graph, start):
start.setDistance(0)
start.setPred(None)
vertQueue = Queue()
vertQueue.enqueue(start)
while (vertQueue.size() > 0):
currentVert = vertQueue.dequeue()
for nbr in currentVert.getConnections():
if (nbr.getColor() == "white") :
nbr.setColor('gray')
nbr.setDistance(currentVert.getDistance() + 1)
nbr.setPred(currentVert)
vertQueue.enqueue(nbr)
currentVert.setColor('black')
def traverse(targetVertex):
x = targetVertex
while (x.getPred()):
print(x.getId(), end=" <- ")
x = x.getPred()
print(x.getId())
sourceFile='/Users/yuanjicai/PycharmProjects/stucture/fourletterwords.txt'
wordgraph = buildWordGraph(sourceFile)
bfs(wordgraph, wordgraph.getVertex('FOOL'))
traverse(wordgraph.getVertex('SAGE'))算法分析 : BFS主体使用两个循环嵌套, while对每个顶点访问一次,所以复杂度为O(\V);而内循环for,由于每条边只有在它的顶点u出队时才会被检查一次,且每个顶点最多出队一次,所以每条边最多被检查1次;
综合起来BFS的时间复杂度为O(\V+\E);创建单词关系图也需要时间,最多为O(\v\^2);回逆时的复杂度为O(n)。
深度优先算法Depth First Search(DFS)
深度优先算法Depth First Search(DFS),它沿着树的的单支尽量深入向下搜索,如果到无法继续的程度还未找到问题的解,就回溯到上一层再搜索下一分支.
算法1: 专门解决骑士周游问题,每个顶点仅访问一次;
算法2: 允许顶点被重复访问,可作为其它图算法的基础,更加通用.
解决思路: 如果沿着单支深入搜索到无法继续(所有合法移动都被走过)时,路径的长度还没达到预定值(8*8-1),那么就清除颜色标记,返回到上一层,然后换一个分支继续深入搜索. 操作过程需要引入栈来记录路径,以便进行回溯操作。
DFS的应用举例--骑士周游问题
解决步骤:
- 首先将合法走棋次序表示为一个图;
- 其次采用图搜索算法搜寻一个长度为(行*列-1)的路径,路径上包含每个顶点恰好一次;
- 将棋盘格做为顶点;按照"马走日"规则的走棋步骤作为连接边;建立每一个棋盘格的所有合法走棋步骤能够到达的棋盘格关系图;
def genLegalMoves(x, y, bdSize):
newMoves = []
# 以当前位置x,y坐标为参考,"马"可以跳的合法相对坐标位置
moveOffsets = [(-1,-2),(-1,2),(-2,-1),(-2,1),(1,-2),(1,2),(2,-1),(2,1)]
for i in moveOffsets:
newX = x + i[0]
newY = y + i[1]
if legalCoord(newX, bdSize) and legalCoord(newY, bdSize):
newMoves.append((newX, newY))
return newMoves
def legalCoord(x, bdSize):
if x >= 0 and x < bdSize:
return True
else:
return False
def buildKnightGraph(bdSize):
ktGraph = Graph()
for row in range(bdSize):
for col in range(bdSize):
nodeId = posToNodeId(row, col, bdSize)
newPostions = genLegalMoves(row, col, bdSize)
for e in newPostions:
nextNodeId = posToNodeId(e[0], e[1], bdSize)
# 当前棋格和下一跳产生关系
ktGraph.addEdge(nodeId, nextNodeId)
return ktGraph
def posToNodeId(row, col, bdsize):
#根据行、列坐标生成棋盘格的id
return row*bdsize+col
def orderByAvail(currentVertex):
# 将当前节点的neighbor排序,按neighbor是否拥有下一个neighbor的规则排序(一种启发式算法)
resList = []
for v in currentVertex.getConnections():
if v.getColor() == 'white':
c = 0
for w in v.getConnections():
if w.getColor() == 'white':
c += 1
resList.append((c,v))
resList.sort(key=lambda x: x[0])
return [y[1] for y in resList]
def knightTour(n, path, currentVertex, limit):
# n表示层次; path使用列表的append和pop方法实现入栈和出栈;
currentVertex.setColor('gray')
path.append(currentVertex) #递归调用 每次都会把当前顶点设置为'灰色',然后先入栈,如果不满足条件再出栈
if n < limit:
# nbrList = list(currentVertex.getConnections())
nbrList = orderByAvail(currentVertex) #返回已经排序的neighbor列表,优先从棋盘边角搜索
i = 0
done = False
while i < len(nbrList) and not done:
if nbrList[i].getColor() == 'white':
done = knightTour(n + 1, path, nbrList[i], limit)
i += 1
if not done:
path.pop() # 如果不满足条件,则把当前顶点从栈中弹出
currentVertex.setColor('white')
else:
done = True
return done
n = 5
kgGraph = buildKnightGraph(n) #生成5行5列的图(棋盘)
resultPath = [] #可行路径
start = 4 #开始搜索的节点
knightTour(0, resultPath, kgGraph.getVertex(start), n * n - 1)
print("可行路径为", end=": ")
for i in range(len(resultPath)): #输出路径
if i != len(resultPath) - 1:
print(resultPath[i].getId(), end=' ->')
else:
print(resultPath[i].getId())另一种比较通用的DFS算法
它需要扩展原Graph类,如下所示:
class DFSGraph(Graph):
def __init__(self):
super().__init__()
self.time = 0
def dfs(self):
for aVertex in self:
aVertex.setColor('white')
aVertex.setPred("None")
for aVertex in self:
if aVertex.getColor() == 'white':
self.dfsvisit(aVertex)
def dfsvisit(self,startVertex):
startVertex.setColor('gray')
self.time += 1
startVertex.setDiscovery(self.time)
for nextVertex in startVertex.getConnections():
if nextVertex.getColor() == 'white':
nextVertex.setPred(startVertex)
self.dfsvisit(nextVertex)
startVertex.setColor('black')
self.time += 1
startVertex.setFinish(self.time)def buildTestGraph():
g = DFSGraph()
list1 = ['A', 'B', 'C', 'D', 'E', 'F']
for i in list1:
g.addVertex(i)
g.addEdge('A', 'B')
g.addEdge('A', 'D')
g.addEdge('B', 'C')
g.addEdge('B', 'D')
g.addEdge('D', 'E')
g.addEdge('E', 'F')
g.addEdge('E', 'B')
g.addEdge('F', 'C')
return g
testGraph = buildTestGraph()
testGraph.dfs()
d1 = {}
l1 = []
for key in testGraph.getVertices():
currentVertex = testGraph.getVertex(key)
d1[currentVertex.getId()] = (currentVertex.getDiscovery(), currentVertex.getFinish())
l1.append((currentVertex.getId(), currentVertex.getDiscovery(), currentVertex.getFinish()))
l1.sort(key=lambda tup: tup[2], reverse=True)
print("深度优先算法(DFS)遍历图后的结果(列表输出方式)如下: %s" % l1)
d2 = sorted(d1.items(), key=lambda tup: tup[1])
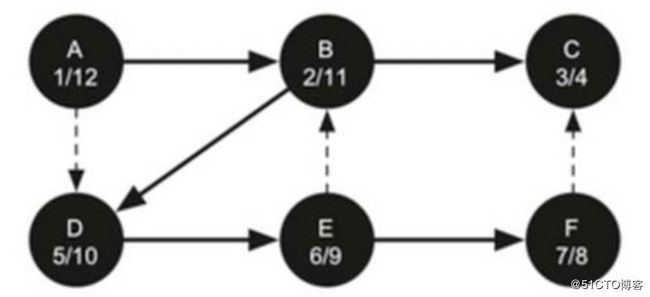
print("深度优先算法(DFS)遍历图后的结果(字典输出方式)如下: %s" % d2)深度优先算法(DFS)遍历图后的结果(列表输出方式)如下: [('A', 1, 12), ('B', 2, 11), ('D', 5, 10), ('E', 6, 9), ('F', 7, 8), ('C', 3, 4)]
深度优先算法(DFS)遍历图后的结果(字典输出方式)如下: [('A', (1, 12)), ('B', (2, 11)), ('C', (3, 4)), ('D', (5, 10)), ('E', (6, 9)), ('F', (7, 8))]Dijkstr算法
Dijkstra首先把起点到所有点的距离存下来找个最短的,然后松弛一次再找出最短的,所谓的松弛操作就是,遍历一遍看通过刚刚找到的距离最短的点作为中转站会不会更近,如果更近了就更新距离,这样把所有的点找遍之后就存下了起点到其他所有点的最短距离。Dijkstra算法只能用于边权为正的图,时间复杂度为O(n^2)。
class PriorityQueue:
def __init__(self):
self.heapArray = [(0,0)]
self.currentSize = 0
def buildHeap(self,alist):
self.currentSize = len(alist)
self.heapArray = [(0,0)]
for i in alist:
self.heapArray.append(i)
i = len(alist) // 2
while (i > 0):
self.percDown(i)
i = i - 1
def percDown(self,i):
while (i * 2) <= self.currentSize:
mc = self.minChild(i)
if self.heapArray[i][0] > self.heapArray[mc][0]:
tmp = self.heapArray[i]
self.heapArray[i] = self.heapArray[mc]
self.heapArray[mc] = tmp
i = mc
def minChild(self,i):
if i*2 > self.currentSize:
return -1
else:
if i*2 + 1 > self.currentSize:
return i*2
else:
if self.heapArray[i*2][0] < self.heapArray[i*2+1][0]:
return i*2
else:
return i*2+1
def percUp(self,i):
while i // 2 > 0:
if self.heapArray[i][0] < self.heapArray[i//2][0]:
tmp = self.heapArray[i//2]
self.heapArray[i//2] = self.heapArray[i]
self.heapArray[i] = tmp
i = i//2
def add(self,k):
self.heapArray.append(k)
self.currentSize = self.currentSize + 1
self.percUp(self.currentSize)
def delMin(self):
retval = self.heapArray[1][1]
self.heapArray[1] = self.heapArray[self.currentSize]
self.currentSize = self.currentSize - 1
self.heapArray.pop()
self.percDown(1)
return retval
def isEmpty(self):
if self.currentSize == 0:
return True
else:
return False
def decreaseKey(self,val,amt):
# this is a little wierd, but we need to find the heap thing to decrease by
# looking at its value
done = False
i = 1
myKey = 0
while not done and i <= self.currentSize:
if self.heapArray[i][1] == val:
done = True
myKey = i
else:
i = i + 1
if myKey > 0:
self.heapArray[myKey] = (amt,self.heapArray[myKey][1])
self.percUp(myKey)
def __contains__(self,vtx):
for pair in self.heapArray:
if pair[1] == vtx:
return True
return False
import sys
def dijkstra(routeGraph,start):
for v in routeGraph:
v.setDistance(sys.maxsize)
pq = PriorityQueue()
start.setDistance(0)
pq.buildHeap([[v.getDistance(), v] for v in routeGraph])
while not pq.isEmpty():
currentVertex = pq.delMin()
for nextVert in currentVertex.getConnections():
newDist = currentVertex.getDistance() + currentVertex.getWeight(nextVert)
if newDist < nextVert.getDistance():
nextVert.setDistance(newDist)
nextVert.setPred(currentVertex)
pq.decreaseKey(nextVert, newDist)def buildRouteGrap():
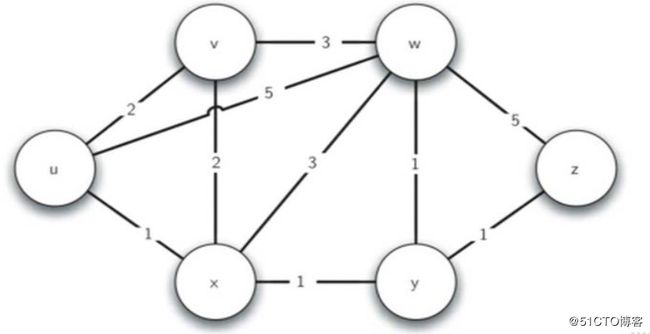
g = Graph()
g.addEdge("u", "v", 2)
g.addEdge("u", "x", 1)
g.addEdge("u", "w", 5)
g.addEdge("v", "w", 3)
g.addEdge("v", "x", 2)
g.addEdge("x", "w", 3)
g.addEdge("x", "y", 1)
g.addEdge("y", "w", 1)
g.addEdge("y", "z", 1)
g.addEdge("w", "z", 5)
return g
routeGraph = buildRouteGrap()
dijkstra(routeGraph, routeGraph.getVertex("u"))
def traversRoute(targetVertex):
if targetVertex.previous:
print(targetVertex.previous.getId(), end="<-")
traverse(targetVertex.previous)
print("Dijkstra后 源路由器 u 到目标路由器 w 的最佳路径是: ", end=" ")
traverse(routeGraph.getVertex('w'))经过dijkstra之后的Graph效果如下: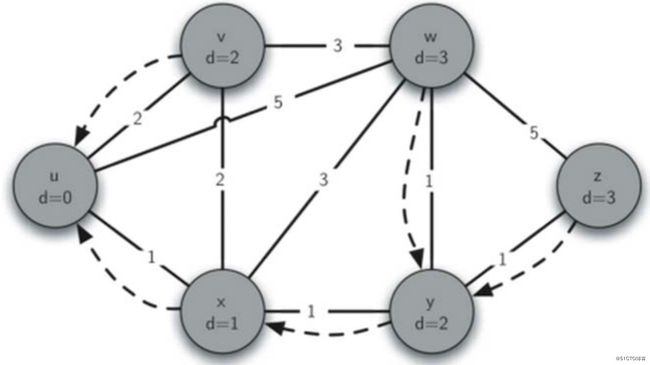
上述代码执行结果如下:
Dijkstra后 源路由器 u 到目标路由器 w 的最佳路径是: w <- y <- x <- u最小生成树(minimum weight spanning tree)
生成树:拥有图中所有顶点和最少数量的边,以保持连通的子图。
图G(V,E)的最小生成树T,定义为包含所有顶点V,以及边E的无圈子集,并且边权重之和最小。
解决最小生成树问题的Prim算法属于"贪心算法",即每步都沿着最小权重的边向前搜索。
def prim(routeGraph, start):
pq = PriorityQueue()
for v in routeGraph:
v.setDistance(sys.maxsize)
v.setPred(None)
start.setDistance(0)
pq.buildHeap([(v.getDistance(), v) for v in routeGraph])
while not pq.isEmpty():
currentVertex = pq.delMin()
for nextVertex in currentVertex.getConnections():
newCost = currentVertex.getWeight(nextVertex)
if nextVertex in pq and newCost < nextVertex.getDistance():
nextVertex.setPred(currentVertex)
nextVertex.setDistance(newCost + currentVertex.getDistance())
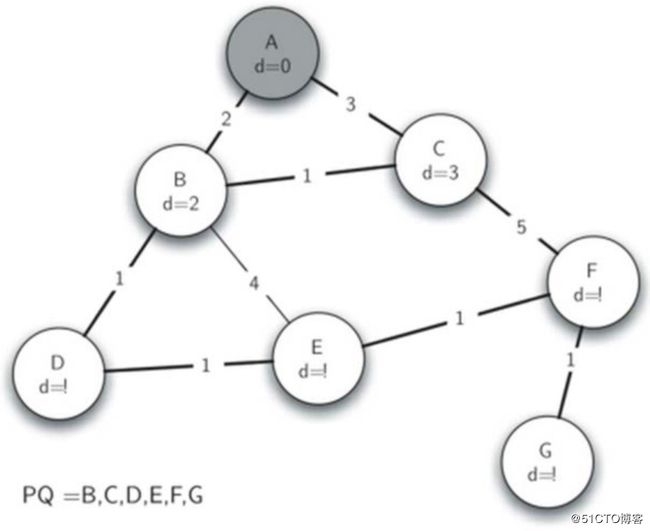
pq.decreaseKey(nextVertex, newCost)def buildRouteGraph2():
g = Graph()
g.addEdge("A", "B", 2)
g.addEdge("A", "C", 3)
g.addEdge("B", "C", 1)
g.addEdge("B", "D", 1)
g.addEdge("B", "E", 4)
g.addEdge("D", "E", 1)
g.addEdge("E", "F", 1)
g.addEdge("C", "F", 5)
g.addEdge("F", "G", 1)
return g
routeGraph2 = buildRouteGraph2()
prim(routeGraph2, routeGraph2.getVertex("A"))
print("prim后 源路由器 A 到目标路由器 G 的最佳路径是: ", end=" ")
traverse(routeGraph2.getVertex('G'))运行结果如下:
prim后 源路由器 A 到目标路由器 G 的最佳路径是: G <- F <- E <- D <- B <- A关于本例中优先队列类的测试如下:
testList = [(4, "a"), (3, "d"), (5, "c"), (2, "e"), (1, "f")]
pq = PriorityQueue()
pq.buildHeap(testList)
# for elem in testList:
# pq.add(elem)
print("本例中优先队列的删除顺序为:", end=" ")
while not pq.isEmpty():
print(pq.delMin(), end=" -> ")输出结果如下:
本例中优先队列的删除顺序为: f -> e -> d -> a -> c ->