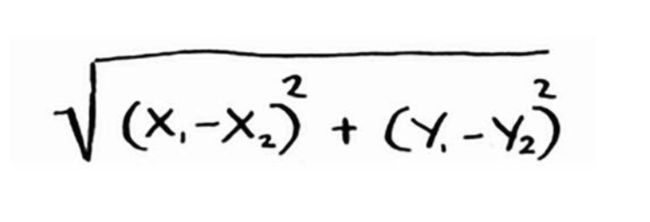算法和数据结构基础一览

概况

数据结构树状图

学好算法和数据结构对培养编程内力很重要

3Points：

1. Chunk it up
2. Deliberate practicing
3. Feedback

知识总览

Data Structure	Algorithm
Array	Greedy
Stack/Queue	Recursion/Backtrace
PriorityQueue（heap）	In-order/Pre-order/Post-order Traversal
LinkedList（single/double）	Breadth-first/Depth-first search
Tree/Binary Tree	Divide and Conquer
Disjoint Set	Dynamic Programming
Trie	Binary Search
BloomFilter	Graph
LRU Cache
Binary Search Tree
Hash Table

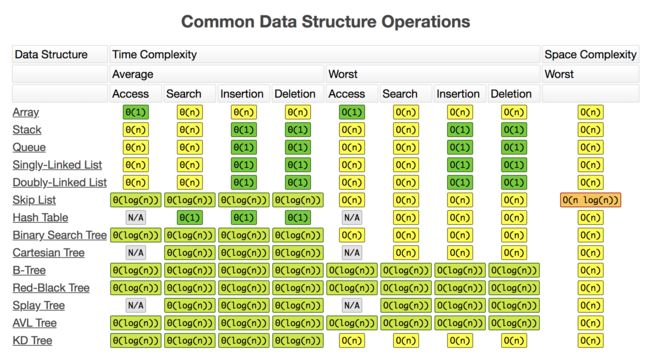
大O表示法 Big O notation

详见：http://bigocheatsheet.com/

各数据结构的时间和空间复杂度

各排序算法的时间和空间复杂度

一、数组 Array

线性表的两种结构

1. 数组是地址连续的
2. Memory Controller 访问任何一个位置的数组下标的时间复杂度 O(1)
3. 插入和删除数组的时间复杂度 O(n)

链表可以改善插入和删除数组的时间复杂度。

二、链表 Linked List

链式存储结构适用场景：

1. 长度未知
2. 频繁进行插入和删除操作

常见操作：

1. 插入 O(1)
   • 找到插入位置
   • 新的节点插入到元素前
   • 把前一个节点的next指针指向新节点
2. 删除 O(1)
   • 前面的节点next指针挪到后一个
   • 把跨越过的节点从内存中删除
3. 查询 O(n)

链表的查询的时间复杂度为O(n)，差于数组等顺序存储结构，所以往往需要根据实际情况来博弈（动态平衡）的选择数据结构，即结合解决问题本身的特点，具体问题具体分析。

习题：数组和链表

1. Leetcode206.反转链表
2. Leetcode24.反转链表相邻节点
3. Leetcode141.判断链表是否有环

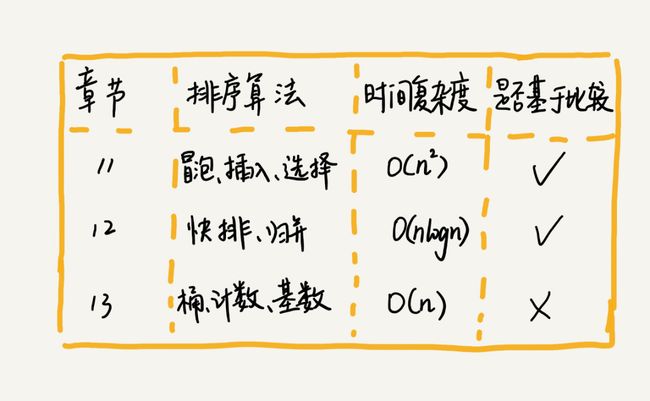
三、排序 Sorting

排序算法时间复杂度一览

思考：在实际的开发中，我们更倾向于使用插入排序算法而不是冒泡排序算法的原因是什么（两者时间复杂度相同）？
答：性能优化更极致

如何分析一个排序算法

排序算法的执行效率

1. 最好情况、最坏情况、平均情况时间复杂度
2. 时间复杂度的系数、常数、低阶
3. 比较次数和交换或移动次数

算法的内存消耗

算法的内存消耗可以用空间复杂度来衡量。

针对排序算法的空间复杂度，引入原地排序的概念，就是特指空间复杂度是O(1)的排序算法。

排序算法的稳定性

如果待排序的序列中存在值相等的元素，经过排序之后，相等元素之间原有的先后顺序不变，叫稳定的排序算法。

冒泡排序

只会操作相邻的两个数据，一次冒泡至少会让一个元素移动到它应该在的位置。包含两个操作子：

1. 比较
2. 交换

优化

当某次冒泡操作已经没有数据交换时，说明已经达到完全有序，不用再执行后续的冒泡操作。

冒泡排序的特征

1. 原地排序
2. 稳定性
3. 时间复杂度：
   最好情况：O(n)
   最坏情况：O(n^2)
   平均时间复杂度：O(n^2)
   可以通过有序度和逆序度来分析：
   • 有序度是数组中具有有序关系的元素对的个数，完全有序的数组有序度叫满有序度n*(n-1)/2；（默认从小到大为有序）
   • 逆序度 = 满有序度 - 有序度

插入排序

动态地往有序集合中添加数据。包含两个操作子：

1. 元素的比较
2. 元素的移动

插入排序的特征

1. 原地排序
2. 稳定性
3. 时间复杂度：
   最好情况：O(n)
   从头到尾遍历已经有序的数据
   最坏情况：O(n^2)
   平均时间复杂度：O(n^2)

选择排序

类似插入排序，但选择排序会每次从未排序区间中找到最小的元素，将其放到已排序区间的末尾。

选择排序的特征

1. 原地排序
2. 不具有稳定性
3. 时间复杂度：
   最好情况、最坏情况、平均情况时间复杂度都为O(n^2)

归并排序

归并排序和快速排序算法更适合大规模的数据排序，两者都用到了分治思想。

分治思想

分治：分而治之，将一个大问题分解成小的子问题来解决。分治算法一般都是用递归实现的，分治是一种解决问题的处理思想，递归是一种编程技巧。

• 利用分治算法求一组数据的逆序对个数

归并排序的递推实现

递推公式：merge_sort(p...r) = merge(merge_sort(p...q)),merge_sort(q+1...r)
终止条件：p >= r

注：合并函数借助哨兵，代码会简洁很多。

归并排序的特征

1. 不是原地排序
   空间复杂度比较高，所以归并排序并没有像快排那样，应用广泛。
2. 稳定性
3. 递归代码的时间复杂度：
   如果定义求解问题 a 的时间是 T(a)，求解问题 b、c 的时间分别是 T(b) 和 T( c)，得到递推关系式：T(a) = T(b) + T(c) + K(K ：将两个子问题 b、c 的结果合并成问题 a 的结果所消耗的时间)。
   所以，递归代码的时间复杂度也可以写成递推公式。
4. 归并排序的时间复杂度：
   T(1) = C； n=1 时，只需要常量级的执行时间，所以表示为 C。
   T(n) = 2*T(n/2) + n； n>1
   可以看出，归并排序的执行效率与要排序的原始数组的有序程度无关，所以其时间复杂度是非常稳定的，不管是最好情况、最坏情况，还是平均情况，时间复杂度都是 O(nlogn)。
5. 归并排序的空间复杂度
   实际上，递归代码的空间复杂度并不能像时间复杂度那样累加。尽管每次合并操作都需要申请额外的内存空间，但在合并完成之后，临时开辟的内存空间就被释放掉了。在任意时刻，CPU 只会有一个函数在执行，也就只会有一个临时的内存空间在使用。临时内存空间最大也不会超过 n 个数据的大小，所以空间复杂度是 O(n)。
6. 归并排序的应用：

• LeetCode21.合并两个有序链表

快速排序 Quicksort

核心思想：

• 分治
• 分区

要使函数不占用很多额外的内存空间，就需要优化快排，即在原地完成分区操作。

优化后快速排序的特征

1. 原地排序
   通过设计巧妙的分区函数，可以实现原地排序，解决了归并排序占用太多内存的问题。
2. 不稳定
3. 快速排序的时间复杂度 O(nlogn)
   快排也是用递归来实现的。如果每次分区操作，都能正好把数组分成大小接近相等的两个小区间，那快排的时间复杂度递推求解公式跟归并是相同的。所以，快排的时间复杂度也是 O(nlogn)。
   但实际上很难实现，极端情况下，快排的时间复杂度就从 O(nlogn) 退化成了 O(n^2)。可以通过合理选择pivot来避免这种情况。

归并排序和快速排序的区别

归并排序和快速排序的区别

归并排序的处理过程：由下到上，即先处理子问题，然后合并。
快速排序的处理过程：由上到下，即先分区，然后再处理子问题。

四、栈和队列 Stack&Queue

Stack	Queue
FILO	FIFO
Array or Linked List	Array or Doubly Linked Lisk

常用队列：消息队列

栈和队列

习题：栈和队列

1. Leetcode20.判断括号性是否合法
2. Leetcode232.225.只用堆栈实现队列/只用队列实现堆栈
3. Leetcode496.下一个更大的元素

优先级队列 PriorityQueue

1. 队列
2. 正常进、按优先级出

实现机制：

1. Heap（Binary，Binomial，Fibonacci）
2. Binary Search Tree（红黑树）

堆 Heap

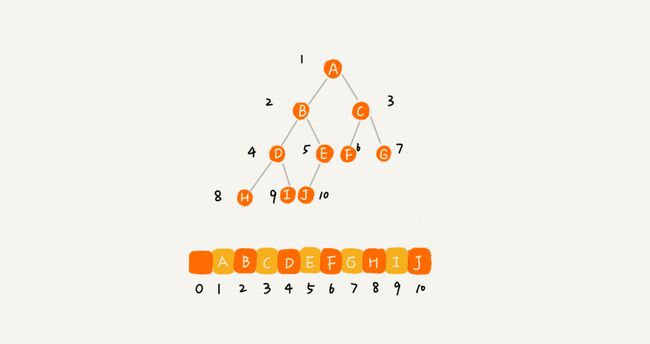
堆就是一种完全二叉树，最常用的存储方式就是数组。

1. 大顶堆：堆中每一个节点的值大于等于子树中每个节点的值。
2. 小顶堆：反之。

堆的操作 - 堆化 Heapify

1. 插入：把新插入的数据放到数组的最后，然后从下往上堆化；
2. 删除：把数组中的最后一个元素放到堆顶，然后从上往下堆化。

插入和删除这两个操作的时间复杂度都是O(logn)。

堆排序

1. 建堆
   将下标从n/2到1的节点，依次进行从上到下的堆化操作，然后就可以将数组中的数据组织成堆这种数据结构。
2. 排序
   迭代地将堆顶的元素放到堆的末尾，并将堆的大小减一，然后再堆化，重复这个过程，直到堆中只剩下一个元素，整个数组中的数据就都有序排列了。

严格的Fibonacci堆相对来说效率最好。

习题：堆

1. Leetcode703.判断数据流中第K大元素 - 求Top K

   解法：维护一个Min Heap

2. Leetcode239.滑动窗口最大值

   解法：

   1. 维护一个Max Heap
   2. (推荐)双端队列deque 时间复杂度O(n)

3. 求中位数

4. 优先级队列

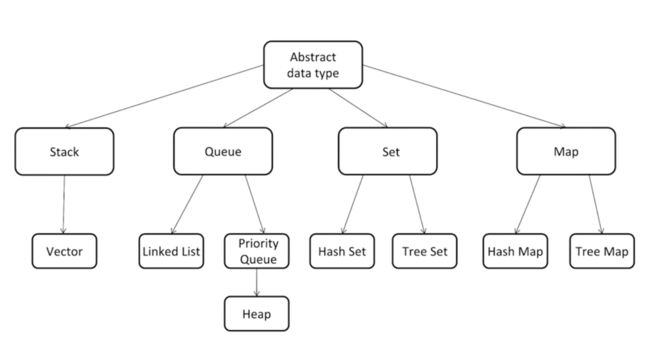
五、映射和集合 Map&Set

哈希表和哈希函数 HashTable&HashFunction

例：30个学生名字放到表里面去，便于查找某一个人，时间复杂度O(1)

不同的英文字符对应不同的下标，一般可以用ASCII码，计算函数为哈希函数

有哈希碰撞的问题

解决：建立一个链表 - 拉链法

List vs Map vs Set

List：数组和链表

Map：建立映射关系（key：value）

Set：不允许有重复的元素

Set可以理解成Map的key或者List去重。

两种映射和集合的实现对比

• HashMap vs TreeMap
• HashSet vs TreeSet
• HashTable vs binary-search-tree

时间复杂度：

Hash：O(1)

Tree：O(log(n))

总结：

1. 对时间复杂度要求高使用哈希表
2. 希望以相对有序的方式储存使用二叉搜索树

习题：映射和集合

1. Leetcode242.有效的字母异位词

   解法：

   1. sort O(nlog(n))
   2. Map计数

2. Leetcode1.两数之和

   解法：

   1. 暴力拆解 O(n^2)
   2. Set x+y=10 O(n)

3. Leetcode15.三数之和

   解法：

   1. 暴力解法
   2. Set
   3. Sort -> Find

4. Leetcode18.四数之和

六、树 Tree

Height、Depth、Level概念区别

举例说明树的高度、深度和层

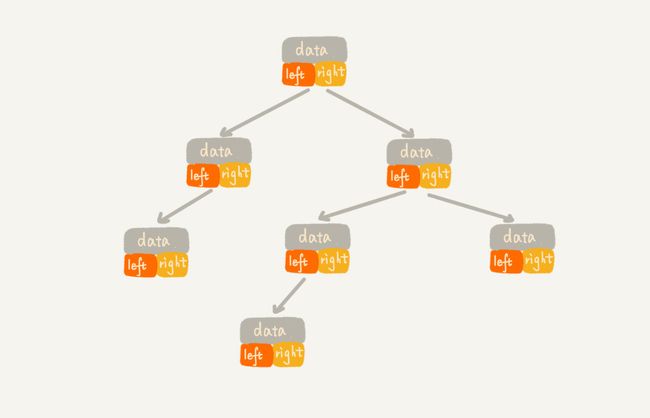
二叉树

特点：

• 每个节点最多只有两个子节点
• 根节点在Level 1
• 满二叉树：
  1. 叶子节点全都在最底层；
  2. 除了叶子节点之外，每个节点都有左右两个子节点。
• 完全二叉树：
  1. 叶子节点都在最底下两层
  2. 最后一层的叶子节点都靠左排列
  3. 除了最后一层，其他层每个节点都有左右两个子节点。
• 实现二叉树的方法

  1. 二叉链式储存法

     
     
     

     二叉链式储存法每个节点有三个字段

  2. 基于数组的顺序储存法

     
     
     

     为了方便计算子节点，根节点会存储在下标为 1 的位置
     
     
     

     非完全二叉树，会浪费比较多的数组存储空间

注：使用顺序存储法，存储一棵完全二叉树，仅仅“浪费”了一个下标为 0 的存储位置。

二叉树的遍历

二叉树的前、中、后序遍历其实是一个递归的过程。
时间复杂度：O(n)

二叉树的遍历

二叉树按层遍历，可以看作以根结点为起点，图的广度优先遍历的问题。

二叉搜索树 Binary Search Tree

也称为二叉查找树、有序二叉树、二叉排序树。支持快速查找、插入、删除数据。
二叉树要求任意一个节点：

• 左子树上所有节点的值均小于它的根节点的值
• 右子树上所有节点的值均大于它的根节点的值
• 以此类推，左右子树均满足条件

二叉搜索树可以是一棵空树。

二叉搜索树的实现

• 遍历

  • 前序遍历

    作用：复制已有二叉树，比重新构造二叉树实现效率要高很多，只需访问所有节点。

  • 中序遍历：可以输出有序的数据序列，默认升序，时间复杂度O(n)，非常高效。

  • 后序遍历

    作用：操作系统和文件系统的遍历

• 查找：

  • 查找给定值：和根节点比较，向左子树或右子树递归

  作用：判断命中

  插入操作和查找操作类似。

• 删除：有三种情况

  • 叶子节点：直接将父节点中，指向要删除节点的指针置为null。
  • 中间节点
    • 只有一个子节点：只需要更新父节点中，指向要删除节点的指针，让它指向要删除节点的子节点。
    • 有两个子节点：
      1. 在被删除的节点右子树中找到最小子节点
      2. 把被删除的值替换成最小子节点
      3. 把最小子节点原位删除

不论是插入、删除还是查找，时间复杂度都跟树的高度成正比，也就是O(height)。理想情况下，时间复杂度是O(logn)。

如果节点的个数是 n，最大层数是L，那么 n 满足：

n >= 1+2+4+8+...+2^(L-2)+1
n <= 1+2+4+8+...+2^(L-2)+2^(L-1)

借助等比数列的求和公式，计算得出，L 的范围是 [log₂(n+1) , log₂n +1]。完全二叉树的层数小于等于log₂n。

支持重复数据的二叉查找树

1. 通过链表和支持动态扩容的数组等数据结构，把值相同的数据都储存在同一个节点上。
2. 把这个新插入的重复数据当作大于这个节点的值来处理，这种方法更优雅。

散列表和二叉树相比二叉树的优势

1. 散列表输出有序数据，需先排序，二叉查找树只需中序遍历
2. 散列表扩容耗时很多，遇到散列冲突时，性能不稳定，平衡二叉查找树的性能非常稳定，时间复杂度稳定在 O(logn)。
3. 散列表哈希冲突和哈希函数的额外耗时，有时很大。
4. 平衡二叉查找树只需要考虑平衡性这一个问题，而且这个问题的解决方案比较成熟、固定。
5. 散列表装载因子不能太大，特别是基于开放寻址法解决冲突的散列表，不然会浪费一定的存储空间。

红黑树 Red-Black Tree - 平衡二叉查找树

极端情况下，二叉树会退化成链表。“平衡”的意思可以等价为性能不退化。“近似平衡”就等价为性能不会退化的太严重。

平衡二叉查找树的严格定义：
二叉树中任意一个节点的左右子树的高度相差不能大于 1。

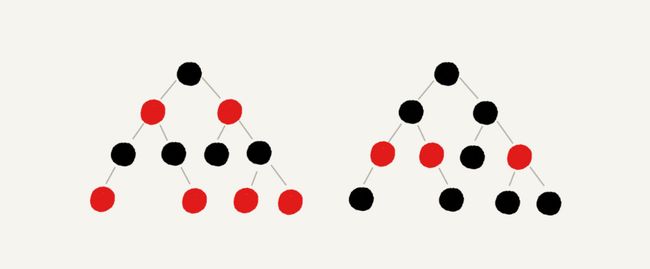
红黑树定义

红黑树的例子

红黑树中的节点，一类被标记为黑色，一类被标记为红色。除此之外，一棵红黑树还需要满足这样几个要求：

• 根节点是黑色的
• 每个叶子节点都是黑色的空节点（NIL），也就是说，叶子节点不存储数据；
• 任何相邻的节点都不能同时为红色，也就是说，红色节点是被黑色节点隔开的；
• 每个节点，从该节点到达其可达叶子节点的所有路径，都包含相同数目的黑色节点；

红黑树没有严格符合上面的定义，它从根节点到各个叶子节点的最长路径，有可能会比最短路径大一倍，但仍是合格的平衡二叉查找树。

红黑树近似平衡，插入、删除、查找操作的时间复杂度都是O(logn)。

递归树

递归代码的时间复杂度分析：

1. 递归树：快排的平均时间复杂度
2. 递推公式：归并排序、快排的最好情况时间复杂度

二叉树的递归前中后序遍历，两者都不适用。

七、图 Graph

树就是特殊化的图。

• 非线性表结构
• 可双向

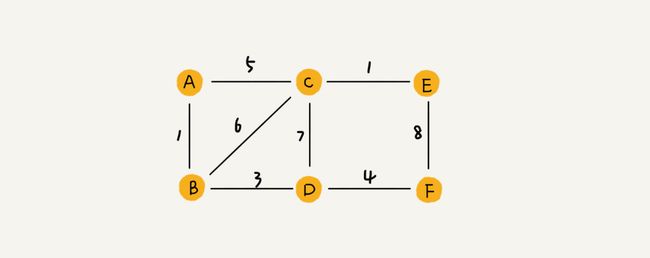
图中的元素叫作顶点（vertex），图中的一个顶点可以与任意其他顶点建立连接关系，把这种建立的关系叫边（edge）。

图的应用

1. 微信（无向图）
   顶点：用户
   边：互加好友
   顶点的度：用户有多少个好友
2. 微博：单向社交关系（有向图）
   入度：粉丝数
   出度：关注数

实现：跳表、邻接表、逆邻接表、哈希算法，除此之外还可以利用外部存储，如数据库。

3. QQ亲密度（带权图）

   
   
   

   每条边都有一个权重 weight

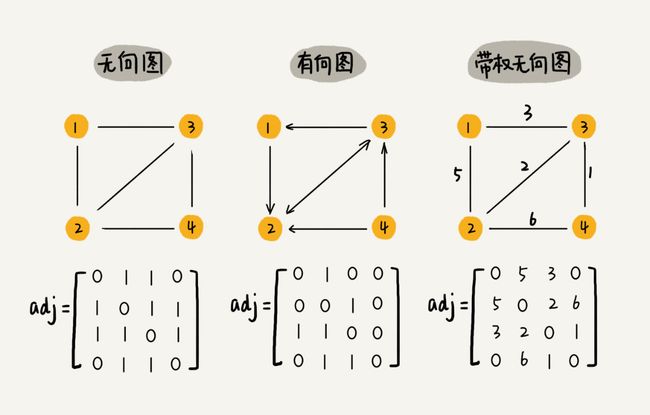
在内存中如何存储图

1. 邻接矩阵 Adjacency Matrix

邻接矩阵的底层依赖一个二维数组

优点：
1. 简单直观
2. 便于获取顶点之间的关系
3. 可以将很多图的运算转换成矩阵之间的运算。比如用Floyd-Warshall 算法求解最短路径，就是利用矩阵循环相乘若干次得到结果。

缺点：比较浪费存储空间

如果存储的是稀疏图（Sparse Matrix），即顶点很多，但每个顶点的边很少，对应到矩阵里就都是0，那邻接矩阵的存储方法就更加浪费空间了。比如：微信。

2. 邻接表 Adjacency List

邻接表中每个顶点对应一条链表

可以将邻接表中的链表改成红黑树或其他更高效的动态数据结构，如平衡二叉树、跳表、散列表。

图的搜索

1. 深度优先搜索 Depth-First-Search
   回溯思想：递归

图上的深度优先搜索算法的时间复杂度是 O(E)，E 表示边的个数。
深度优先搜索算法的消耗内存主要是 visited、prev 数组和递归调用栈。visited、prev 数组的大小跟顶点的个数 V 成正比，递归调用栈的最大深度不会超过顶点的个数，所以总的空间复杂度就是 O(V)。

2. 广度优先搜索 Breadth-First-Search
   思想：适用于非加权图中查找最短路径

   
   
   

   BFS是“地毯式”层层推进的搜索

广度优先搜索的时间复杂度也可以简写为O(E)。广度优先搜索的空间消耗主要在几个辅助变量 visited 数组、queue 队列、prev 数组上。这三个存储空间的大小都不会超过顶点的个数，所以空间复杂度是 O(V)。

优化：检查完一个元素之后，应将其标记为已检查或使用列表记录，以防死循环。
应用：

• 给你一个用户，找出这个用户的所有三度好友关系；
• 编写拼写检查器，计算最少编辑多少个地方就可将错拼的单词改成正确的单词；
• 编写跳棋AI，计算最少走多少步就可获胜。

3. A*
4. IDA*

八、递归 Recursion

关键：写出递推公式，找到终止条件

递归需要满足的三个条件

1. 一个问题的解可以分解为几个子问题的解
2. 该问题与分解之后的子问题，除了数据规模不同，求解思路完全一致
3. 存在递归终止条件

递归优点

高效，简洁

递归注意事项

1. 警惕堆栈溢出
   解决方案：限制递归调用的最大深度

该解决方案不能完全解决问题，因为最大允许的递归深度跟当前线程剩余的栈空间大小有关，事前无法计算。如果实时计算，代码过于复杂，就会影响代码的可读性。如果深度大小比较小，可以用该方案。

2. 警惕重复计算
   解决方案：通过一个数据结构（比如散列表）来保存已经求解过的f(k)。当递归调用f(k)时，先看下是否已经求解过了。如果是，则直接从散列表中取值返回，不需要重复计算。
3. 函数调用的数量较大时，就会积聚成一个可观的时间成本。
4. 递归调用一次就会在内存栈中保存一次现场数据，在分析递归代码空间复杂度时，需要额外考虑这部分花销。

注：几乎所有的递归代码都可以改为迭代循环的非递归写法，但本质没有变。

递归代码调试

1. 打印日志发现，递归值
2. 结合条件断点进行调试

递归代码常见业务场景应用

1. 给定用户ID，查找这个用户的最终推荐人
   该问题中要处理由于数据库里存在脏数据，而产生的无限递归问题。解决方式是自动检测环的存在。

九、散列表 Hash Table

散列思想

散列表用的是数组支持按照下标随机访问数据的时候，时间复杂度是O(1)的特性，通过散列函数把元素的键值映射为下标，然后将数据存储在数组中对应的下标的位置。所以，散列表其实是数组的一种扩展。

• 用来标识的字段叫键(key)或关键字。
• 把标识字段转化为数组下标的映射方法就叫做散列函数。
• 散列函数计算得到的值叫做散列值。

散列函数的设计

可以把它定义成hash(key)，表示经过散列函数计算得到的散列值。
散列函数设计的基本要求：

1. 散列函数计算得到的散列值是一个非负整数；
2. 如果 key1 = key2，那 hash(key1) == hash(key2)；
3. 如果 key1 ≠ key2，那 hash(key1) ≠ hash(key2)。

注：即便像业界著名的MD5、SHA、CRC等哈希算法，也无法完全避免散列冲突。

解决散列冲突

1. 开放寻址法
   • 线性探测 Linear Probing
     注意：不能单纯地把要删除的元素设置为空，因为如果这个空闲位置是后来删除的，就会导致原来的查找算法失效。解决方案是，特别处理将删除的元素，标记为deleted。
     散列表插入数据越来越多时，线性探测的时间就会越来越久。
   • 二次探测 Quadratic probing
     探测的步长是原来的“二次方”，探测的下标序列就是 hash(key)+0，hash(key)+1^2， hash(key)+2^2 ...
   • 双重散列 Double hashing
     使用一组散列函数hash1(key)，hash2(key)，hash3(key)…先用第一个散列函数，如果计算得到的存储位置已经被占用，再用第二个散列函数，依次类推，直到找到空闲的存储位置。

装载因子用来表示空位的多少，计算公式为：散列表的装载因子 = 填入表中的元素个数 / 散列表的长度。
装载因子越大，说明空闲位置越少，冲突发生的可能性越大，散列表的性能越低。
不错的经验规则是：当填装因子大于0.7，就给散列表 resizing。

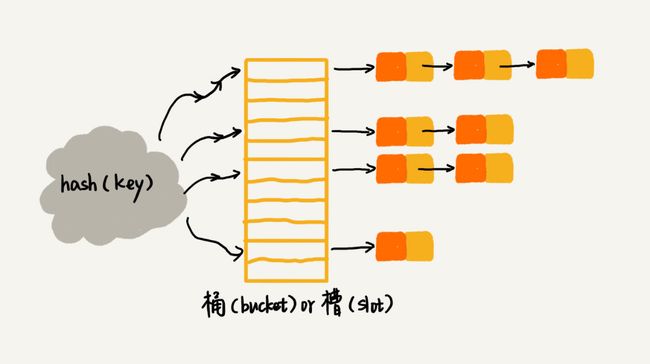
2. 链表法
   一种更加常用的散列冲突解决办法，比开放寻址法简单很多。在散列表中，每个“桶（bucket）”或者“槽（slot）”会对应一条链表，所有散列值相同的元素我们都放到相同槽位对应的链表中。
   
   

   链表法解决散列冲突原理
   
   插入：通过散列函数计算出对应的散列槽位，将其插入到对应链表。时间复杂度O(1)
   查找、删除：通过散列函数计算出对应的散列槽位，遍历链表查找或者删除。时间复杂度跟链表的长度k成正比，即O(k)。

散列比较均匀的散列函数来说，理论上讲，k=n/m，其中 n 表示散列中数据的个数，m 表示散列表中“槽”的个数。

散列冲突解决方法的选择

开放寻址法
优点：

• 有效利用CPU
• 序列化简单

缺点：

• 冲突代价高
• 较浪费内存空间
  适用范围：当数据量比较小、装载因子小的时候，适合采用开放寻址法。这也是 Java 中的使用开放寻址法解决散列冲突的原因。

链表法
优点：

1. 内存利用率高
2. 对大装载因子的容忍度更高

缺点：

1. 储存比较小的对象，比较消耗内存
2. 对CPU缓存不友好

大部分情况下，链表法更加普适。可以将链表法改造为其他高效的动态数据结构，比如：跳表、红黑树。

设计工业级散列表

满足条件：

1. 不复杂，支持快速的查询、插入、删除操作；
2. 内存占用合理，不能浪费过多的内存空间；
3. 生成的值随机、平均，性能稳定，在极端情况下，散列表的性能也不会退化到无法接受的情况。

设计思路：

1. 合适的散列函数
2. 定义装载因子阈值，并且设计动态扩容策略
3. 选择合适的散列冲突解决方法

避免低效的扩容：为了解决一次性扩容耗时过多的情况，可以通过这样均摊的方法，将一次性扩容的代价，均摊到多次插入操作中，就避免了一次性扩容耗时过多的情况。这种实现方式，任何情况下，插入一个数据的时间复杂度都是 O(1)。

为何散列表和链表经常一块使用

• 散列表是无规律存储的，无法支持按照某种顺序快速地遍历数据。
• 将散列表中的数据拷贝到数组中，然后排序，再遍历，就可以按照顺序遍历散列表中的数据。
• 散列表是动态数据结构，每当希望按顺序遍历散列表中的数据的时候，都需要先排序，那效率势必会很低。
  以上，就是经常将散列表和双向链表（或者跳表）结合在一起使用的原因。

应用：

1. LRU Cache 缓存淘汰算法
2. Redis 有序集合
3. Java LinkedHashMap
4. YYMemoryCache
5. DNS resolution
6. 查重
7. 创建搜索引擎：反向索引(inverted index)

散列表中，将单词或记录作为索引，将文档ID作为记录的数据结构被称为反向索引(inverted index)。

哈希算法

MD5、SHA

1. 从哈希值不能反向推导出原始数据（所以哈希算法也叫单向哈希算法
2. 对输入数据非常敏感，哪怕原始数据只修改了一个 Bit，最后得到的哈希值也大不相同；
3. 散列冲突的概率要很小，对于不同的原始数据，哈希值相同的概率非常小；
4. 哈希算法的执行效率要尽量高效，针对较长的文本，也能快速地计算出哈希值。

哈希算法的应用：

• 安全加密
• 唯一标识：大数据信息摘要
  如：开头，中间，最后各取100字节，MD5加密
• 数据校验：校验数据的完整性和正确性，字符串匹配
• 散列函数
  简单，追求效率
• 负载均衡：实现会话粘滞的负载均衡策略
• 数据分片：多机分布式处理
• 分布式存储：一致性哈希算法

其他用户信息安全防范：

• 防范字典攻击
  引入一个salt，跟用户的密码组合在一起，增加密码的复杂度。拿组合之后的字符串来做哈希算法加密，将它存储到数据库中，进一步增加破解的难度。

安全和攻击是一种博弈关系，不存在绝对的安全。所有的安全措施，只是增加攻击的成本而已。

十、并查集 Disjoint Sets

并查集思想

并查集是一种用于处理一些不交集合（Disjoint Sets）的合并（merge）和查询（find）问题的数据结构。

应用

1. 判断无向图中是否出现回路
2. Kruskal法最小生成树

十一、Trie树

Trie树思想

又称字典树，是一种多叉树结构。比较小耗内存，是空间换时间的典型例子。

应用

1. 查找前缀匹配的字符串
2. 搜索关键词提示

十二、算法思想

贪心算法 Greedy algorithom

思想：每步都选择局部最优解。
时间复杂度：O(n^2)
应用：分糖果、钱币找零、区间覆盖

属于贪心算法的有：

1. 霍夫曼编码 Huffman Coding
   实现数据压缩编码，有效节省数据存储空间

2. Prim

3. Kruskal 最小生成树算法

4. Dijkatra's algorithm 单源最短路径算法

   如果图中包含负权边，应使用贝尔曼-福德算法。

   思想：适用于有向无环图
   应用：加权图 中计算某种度量指标最小的策略
   步骤：

   1. 找出最短时间内前往的节点
   2. 更新该节点邻居的开销
   3. 对所有节点重复这个过程
   4. 计算最终路径

注意识别NP完全问题，要使用近似求解来解决。

分治算法 Divide and conquer

核心思想：分而治之

应用：

1. 短时间内解决海量数据处理问题：MapReduce
   MapReduce也是特殊的并行算法，即分布式算法。可让算法在多台计算机上运行，可以通过Apache Hadoop实现。

   MapReduce给予两个简单的理念：映射(map)函数和归并函数(reduce)，映射是将一个数组转化成另一个数组，而归并是将一个数组转换为一个元素。

2. 降低问题求解的时间复杂度

习题：

1. LeetCode169.求众数

回溯算法 Backtracking

回溯法就是对隐式图的深度优先搜索算法。

核心思想：解决广义的搜索问题，非常适合用递归来实现。利用剪枝，我们并不需要穷举搜索所有的情况，从而提高搜索效率。

应用：

1. 数独
2. 八皇后问题
3. 0-1背包问题
4. 图否着色
5. 旅行商问题
6. 全排列
7. 正则表达式

动态规划 Dynamic Programming

核心思想：把问题分解为多个阶段，每个阶段对应一个决策。记录每一个阶段可达的状态集合，然后通过当前阶段的状态集合，来推导下一个阶段的状态集合，动态地往前推进。

应用：

1. 0-1 背包问题
2. 双十一凑单问题
3. 最小路径和
4. 查找两个字符串的最长公共子序列
5. 一个数据序列的最长递增子序列
6. git diff命令
7. Word

习题：

1. LeetCode121.买卖股票的最佳时机

动态规划需要满足每个子问题都是离散的，即不依赖于其他子问题时使用，每一种动态方案都涉及网格。动态规划的本质其实是空间换时间。

拓扑排序 Topological Sorting

思想：基于有向无环图
实现：

1. Kahn 算法
   从图中，找出一个入度为 0 的顶点，将其输出到拓扑排序的结果序列中，并且把这个顶点可达的顶点的入度都减 1。循环执行上面的过程，直到所有的顶点都被输出。最后输出的序列，就是满足局部依赖关系的拓扑排序。
2. DFS 深度优先搜索算法
   遍历图中的所有顶点，而非只是搜索一个顶点到另一个顶点的路径。
   1. 通过邻接表构造逆邻接表
   2. 递归处理每个顶点

应用：

1. 确定代码文件的编译依赖关系
2. 检测环的存在
3. 根据图创建一个有序列表

K最近临算法 k-nearest neighbours，KNN

过程：

1. 分类：编组
2. 特征提取：物品 -> 一系列可比较的数字。
   在挑选合适的特征方面，没有放之四海皆准的法则。
   计算两点的距离，可以使用毕达哥拉斯公式：
   
   

   毕达哥拉斯公式

实际开发中经常使用余弦相似度(cosine similarity)，余弦相似度不计算两个矢量的距离，而比较它们的角度。

3. 回归：预测结果

应用：

1. OCR 算法：光学字符识别(optical character recognition)
   OCR的第一步是查看大量的数字图像并提取特征，这被称为训练(training)。
2. 垃圾邮件过滤器
   算法：朴素贝叶斯分类器(Naive Bayes classifier)
3. 预测股票市场 - 这几乎是不可能完成的任务~

傅里叶变换

傅里叶变换非常适合用于处理数字信号，包括用来压缩音乐和音频频率分解。首先将音频文件分解为音符，该算法能准确地提取出对整个音乐贡献大的音符，并弱化不重要的音符。

数字信号不只是音乐，还可以处理图片的压缩格式JPG或者用来地震预测和DNA分析。

并行算法

并行算法与海量数据处理相关，能极大改善性能和可扩展性。

在最佳情况下，排序算法的速度大致为O(nlogn)。众所周知，对数组 进行排序时，除非使用并行算法，否则运行时间不可能为O(n)。对数组进行排序时，快速排序的并行版本所需的时间为O(n)。

设计并行算法很难，而且提升速度并非线性的，原因是：

1. 并行性管理开销：例如，分配处理之后合并也是需要时间的。
2. 负载均衡

位图 BitMap

位图思路

通过位运算，每一个元素用一个二进制位bit表示，通过数组下标查询。

应用

1. 爬虫避免重复爬取
2. 布隆过滤器：位图的改进

布隆过滤器 BloomFilter

布隆过滤器是一个很长的二进制向量和一系列随机和复杂的hash函数，可以用于检索一个元素是否在一个集合中，是一种概率型数据结构。
优点：占用的存储空间少。
应用：

1. Reddit 检查文章是否发布过
2. Google 检查网站是否被搜集过
3. 为用户提示可能的恶意网站：可能将正常网站标记为疑似恶意误判（由经过K个hash函数处理导致），但不会漏报。
4. 统计大型网站的UV数

HyperLogLog

HyperLogLog是一种类似于布隆过滤器的算法。

场景：Google要计算用户执行的不同搜索的数量，或者Amazon要计算当天用户浏览的不同商品的数量，需要耗用大量的空间。对Google来说，必须有一个日志，其中包含用户执行的不同搜索。有用户执行搜索时，Google 必须判断该搜索是否包含在日志中：如果答案是否定的，就必须将其加入到日志中。即便只记录一天的搜索，这种日志也非常之大。

HyperLogLog近似地计算集合中不同的元素数，与布隆过滤器一样，它不能给出准确的答案， 但也八九不离十，而占用的内存空间却少得多。

SHA 算法

前面提到的散列算法中的一种，安全散列算法(secure hash algorithm，SHA)。重要特征是局部不敏感。
应用：

1. 大文件比较
2. 检查密码：SHA-2或SHA-3、此外还有bcrypt

局部敏感散列函数：Simhash。可以来判断网页是否已搜集、论文查重、过滤版权纠纷的内容。

Diffie-Hellman

1. 公钥
2. 私钥

替代：RSA

线性规划

线性规划用于在给定约束条件下最大限度地改善指定的指标，解决最优化问题。
思想：Simplex算法

最短路径 Shortest Path Algorithm

单源最短路径算法：
Dijkstra 算法
利用堆操作完成

概率统计 - 朴素贝叶斯分类器 Naive Bayes classifier

过滤器的两种方法：

1. 基于黑名单的过滤器
2. 基于规则的过滤器

• 包含特殊词汇
• 群发号码
• 包含回拨的联系号码
• 格式花哨、内容很长
• 符合已知垃圾短信的模板

超过某个阈值，才会被判重。可以基于概率统计的方法，找出单词出现在垃圾短信中的概率。

弊端：垃圾短信发送人员针对性躲避规则

3. 基于概率统计的过滤器（推荐）

   
   
   

   朴素贝叶斯算法

结合场景和以上三种方法，不断调整策略，才会使判定更准确。

向量空间 - 欧几里得距离 Euclidean distance

歌曲推荐方法：

1. 基于相似用户推荐

   
   
   

   欧几里得距离
2. 基于相似歌曲推荐
   对于两首歌，如果喜欢听的人群都是差不多的，那侧面就可以反映出，这两首歌相似。

B+树

二叉查找树->B树->B+树
思路：构建m叉树
应用：数据库的索引
优点：降低了磁盘I/O操作
特点：

• 每个节点中子节点的个数不能超过 m，也不能小于 m/2（B树）
• 根节点的子节点个数可以不超过 m/2，这是一个例外
• m 叉树只存储索引，并不真正存储数据。
• 通过链表将叶子节点串联在一起，这样可以方便按区间查找
• 一般情况，根节点会被存储在内存中，其他节点存储在磁盘中。

伸展树 Splay Tree

一种能够自我平衡的二叉查找树，它能在均摊的时间内完成基于伸展操作的插入、查找、修改和删除操作。