前言
本篇主要讲坐标旋转及其应用,这是编程动画必不可少的技术。
阅读本篇前请先打好前面的基础。
本人能力有限,欢迎牛人共同讨论,批评指正。
坐标旋转
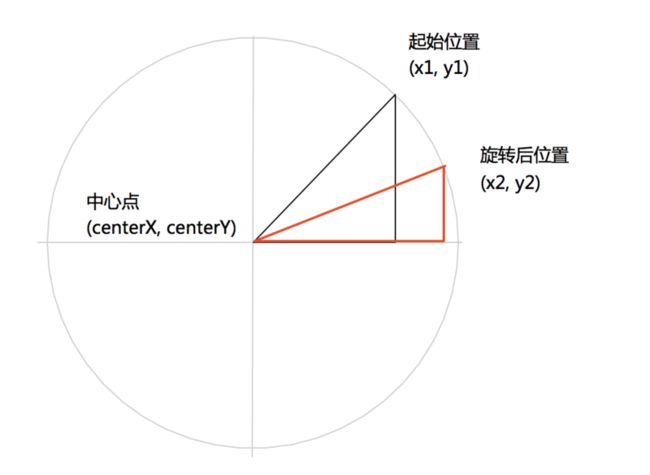
模拟场景:已知一个中心点(centerX,centerY),旋转前物体ball(x1,y1),旋转弧度(rotation);求旋转后物体(x2,y2)。(如下图)
坐标旋转就是说围绕某个点旋转坐标,我们要依据旋转的角度(弧度),计算出物体旋转前后的坐标,一般有两种方法:
简单坐标旋转
灵活运用前章节的三角函数知识可以很容易解决,基本思路:
- 计算物体初始相对于中心点的位置;
- 使用atan2计算弧度angle;
- 使用勾股定理计算半径radius;
- angle+rotation后使用cos计算旋转后x轴位置,用sin计算旋转后y轴位置。
下面是示例是采用这种方法的圆周运动,其中vr为ball相对于中心点的弧度变化速度,由于旋转半径是固定的,所以没有在动画循环里每次都获取。
完整示例:简单坐标旋转演示
/**
* 简单坐标旋转演示
* */
window.onload = function () {
const canvas = document.getElementById('canvas');
const context = canvas.getContext('2d');
const ball = new Ball();
ball.x = 300;
ball.y = 200;
// 弧度变化速度
const vr = 0.05;
// 中心点位置设定在画布中心
const centerX = canvas.width / 2;
const centerY = canvas.height / 2;
// ball相对与中心点的距离
const dx = ball.x - centerX;
const dy = ball.y - centerY;
// ball相对与中心点的弧度
let angle = Math.atan2(dy, dx);
// 旋转半径
const radius = Math.sqrt(dx ** 2 + dy ** 2);
(function drawFrame() {
window.requestAnimationFrame(drawFrame, canvas);
context.clearRect(0, 0, canvas.width, canvas.height);
ball.x = centerX + Math.cos(angle) * radius;
ball.y = centerY + Math.sin(angle) * radius;
angle += vr;
ball.draw(context);
}());
};坐标旋转公式
上面的方法对于单个物体来说是很合适的,特别是角度和半径只需计算一次的情况。但是在更动态的场景中,可能需要旋转多个物体,而他们相对于中心点的位置各不相同。所以每一帧都要计算每个物体的距离、角度和半径,然后把vr累加在角度上,最后计算物体新的坐标。这样显然不会是优雅的做法。
理想的做法是用数学方法推导出旋转角度与位置的关系,直接每次代入计算即可。推导过程如下图:
其实推导过程不重要,我们只需要记住如下两组公式,其中dx2和dy2是ball结束点相对于中心点的距离,所以得到物体结束点,还要分别加上中心点坐标。
// 正向选择
dx2 = (x1 - centerX) * cos(rotation) - (y1 - centerY) * sin(rotation)
dy2 = (y1 - centerY) * cos(rotation) + (x1 - centerX) * sin(rotation)
// 反向选择
dx2 = (x1 - centerX) * cos(rotation) + (y1 - centerY) * sin(rotation)
dy2 = (y1 - centerY) * cos(rotation) - (x1 - centerX) * sin(rotation)下面是示例是采用这种方法的圆周运动,其中dx1和dy1是ball起始点相对于中心点的距离,dx2和dy2是ball结束点相对于中心点的距离。
完整示例:高级坐标旋转演示
/**
* 高级坐标旋转演示
* */
window.onload = function () {
const canvas = document.getElementById('canvas');
const context = canvas.getContext('2d');
const ball = new Ball();
ball.x = 300;
ball.y = 200;
// 弧度变化速度
const vr = 0.05;
// 中心点位置设定在画布中心
const centerX = canvas.width / 2;
const centerY = canvas.height / 2;
// 由于vr是固定的可以先计算正弦和余弦
const cos = Math.cos(vr);
const sin = Math.sin(vr);
(function drawFrame() {
window.requestAnimationFrame(drawFrame, canvas);
context.clearRect(0, 0, canvas.width, canvas.height);
// ball相对与中心点的距离
const dx1 = ball.x - centerX;
const dy1 = ball.y - centerY;
// 代入公式求出ball在结束相对与中心点的距离
const dx2 = dx1 * cos - dy1 * sin;
const dy2 = dy1 * cos + dx1 * sin;
// 求出x2,y2
ball.x = centerX + dx2;
ball.y = centerY + dy2;
ball.draw(context);
}());
};斜面反弹
前面的章节中我们介绍过越界的一种处理办法是反弹,由于边界是矩形,反弹面垂直或水平,所以可以直接将对应轴的速度取反即可,但对于非垂直或水平的反弹面这种方法是不适用的。
坐标旋转常见的应用就是处理这种情况,将不规律方向的复杂问题简单化。
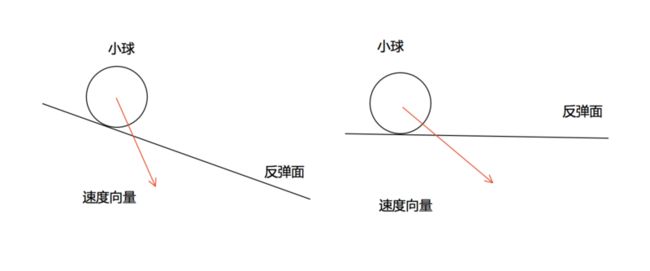
基本思路:(旋转前后如图)
- 使用旋转公式,旋转整个系统,将斜面场景转变为水平场景;
- 在水平场景中处理反弹;
- 再旋转回来。
示例是一个球掉落到一条线上,球受到重力加速度影响下落,碰到斜面就会反弹,每次反弹都会损耗速度。
完整示例:斜面反弹示例
window.onload = function () {
const canvas = document.getElementById('canvas');
const context = canvas.getContext('2d');
const ball = new Ball();
// line类构造函数参数(开始点x轴坐标,开始点y轴坐标,结束点x轴坐标,结束点y轴坐标)
const line = new Line(0, 0, 500, 0);
// 设置重力加速度
const gravity = 0.2;
// 设置反弹系数
const bounce = -0.6;
ball.x = 100;
ball.y = 100;
line.x = 0;
line.y = 200;
line.rotation = 10 * Math.PI / 180;
const cos = Math.cos(line.rotation);
const sin = Math.sin(line.rotation);
(function drawFrame() {
window.requestAnimationFrame(drawFrame, canvas);
context.clearRect(0, 0, canvas.width, canvas.height);
ball.vy += gravity;
ball.x += ball.vx;
ball.y += ball.vy;
// 获取ball与line的相对位置
let x1 = ball.x - line.x;
let y1 = ball.y - line.y;
// 旋转坐标系(反向)
let y2 = y1 * cos - x1 * sin;
// 依据旋转值执行反弹
if (y2 > -ball.radius) {
// 旋转坐标系(反向)
const x2 = x1 * cos + y1 * sin;
// 旋转速度(反向)
const vx1 = ball.vx * cos + ball.vy * sin;
let vy1 = ball.vy * cos - ball.vx * sin;
y2 = -ball.radius;
vy1 *= bounce;
// 将所有东西回转(正向)
x1 = x2 * cos - y2 * sin;
y1 = y2 * cos + x2 * sin;
ball.vx = vx1 * cos - vy1 * sin;
ball.vy = vy1 * cos + vx1 * sin;
ball.x = line.x + x1;
ball.y = line.y + y1;
}
ball.draw(context);
line.draw(context);
}());
};