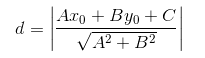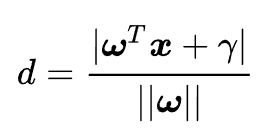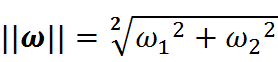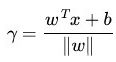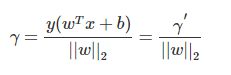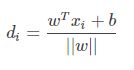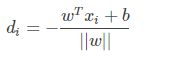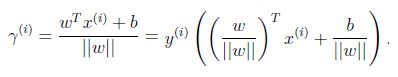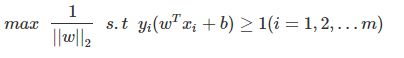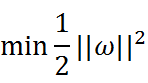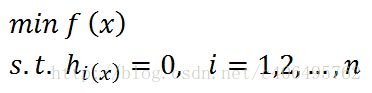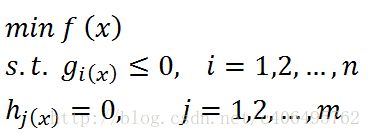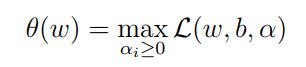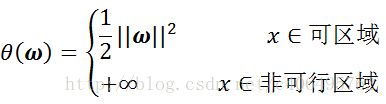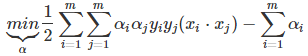SVM(support vector machine)简单的说是一个分类器,并且是一种线性分类和非线性分类都支持的二元分类算法,但经过演变,现在也支持多分类问题,也能应用到了回归问题。Vector:通俗说就是点,或是数据。Machine:也就是classifier,也就是分类器。它的基本模型是定义在特征空间上的间隔最大的线性分类器,间隔最大使它有别于感知机;SVM还包括核技巧,这使它成为实质上的非线性分类器。SVM的的学习策略就是间隔最大化,可形式化为一个求解凸二次规划的问题,也等价于正则化的合页损失函数的最小化问题。SVM的的学习算法就是求解凸二次规划的最优化算法。
支持向量机学习方法包括构建由简至繁的模型:线性可分支持向量机、线性支持向量机及非线性支持向量机。当训练数据线性可分时,通过硬间隔最大化,学习一个线性的分类器,即线性可分支持向量机,又称为硬间隔支持向量机;当训练数据近似线性可分时,通过软间隔最大化,也学习一个线性的分类器,即线性支持向量机,又称为软间隔支持向量机;当训练数据线性不可分时,通过使用核技巧及软间隔最大化,学习非线性支持向量机。
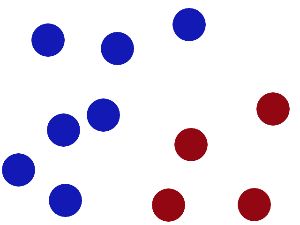
首先通过网络上一个浅显的故事认识SVM:在很久以前的情人节,大侠要去救他的爱人,但魔鬼和他玩了一个游戏。魔鬼在桌子上似乎有规律放了两种颜色的球,说:“你用一根棍分开它们?要求:尽量在放更多球之后,仍然适用。”
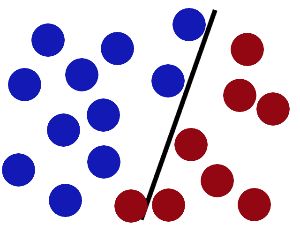
于是大侠这样放,干的不错?
然后魔鬼,又在桌上放了更多的球,似乎有一个球站错了阵营。
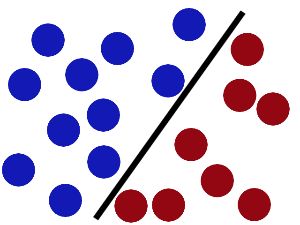
SVM就是试图把棍放在最佳位置,好让在棍的两边有尽可能大的间隙。
现在即使魔鬼放了更多的球,棍仍然是一个好的分界线。
然后,在SVM 工具箱中有另一个更加重要的 trick。 魔鬼看到大侠已经学会了一个trick,于是魔鬼给了大侠一个新的挑战。
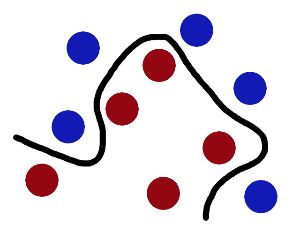
现在,大侠没有棍可以很好帮他分开两种球了,怎么办呢?当然像所有武侠片中一样大侠桌子一拍,球飞到空中。然后,凭借大侠的轻功,大侠抓起一张纸,插到了两种球的中间。
现在,从魔鬼的角度看这些球,这些球看起来像是被一条曲线分开了。
总结上面的小故事,把这些球叫做「data」数据集,把棍子叫做「classifier」分类器, 最大间隙trick叫做「optimization」优化, 拍桌子叫做「kernelling」核函数, 那张纸叫做「hyperplane」超平面。当一个分类问题,数据是线性可分的,也就是用一根棍就可以将两种小球分开的时候,我们只要将棍的位置放在让小球距离棍的距离最大化的位置即可,寻找这个最大间隔的过程,就叫做最优化。但是,现实往往是很残酷的,一般的数据是线性不可分的,也就是找不到一个棍将两种小球很好的分类。这个时候,我们就需要像大侠一样,将小球拍起,用一张纸代替小棍将小球进行分类。想要让数据飞起,我们需要的东西就是核函数(kernel),用于切分小球的纸,就是超平面。
支持向量机的基本思想:
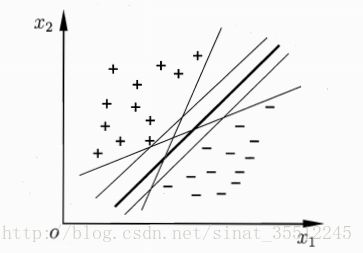
给定训练样本集D=(x1,y1),(x2,y2),......(xm,ym),y∈−1,+1D=(x1,y1),(x2,y2),......(xm,ym),y∈−1,+1,分类学习最基本的想法就是基于训练集D在样本空间中找到一个超平面,将不同类别的样本分开。但是正如下图所示,能将训练样本分开的超平面可能有很多,那我们应该选择哪一个呢?
直观上看,我们应该去找位于两类训练样本“正中间”的超平面,也就是样本点与直线的距离最大那条直线。因为该超平面对训练样本局部扰动的容忍性最好。 支持向量机学习的基本思想是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。大白话:距离超平面最近的那些点(支持向量)离超平面尽可能远
在各种机器学习算法中,SVM是对数学要求较高的一种,一直以来不易被初学者掌握。接下来我们用一张图来把握住推导的整体思路,降低理解的难度。
最简单的SVM从线性分类器导出,根据最大化分类间隔的目标,我们可以得到线性可分问题的SVM训练时求解的问题。但现实应用中很多数据是线性不可分的,通过加入松弛变量和惩罚因子,可以将SVM推广到线性不可分的情况,具体做法是对违反约束条件的训练样本进行惩罚,得到线性不可分的SVM训练时优化的问题。这个优化问题是一个凸优化问题,并且满足Slater条件,因此强对偶成立,通过拉格朗日对偶可以将其转化成对偶问题求解。
到这里为止,支持向量机还是一个线性模型,只不过允许有错分的训练样本存在。通过核函数,可以将它转化成非线性模型,此时的对偶问题也是一个凸优化问题。这个问题的求解普遍使用的是SMO算法,这是一种分治法,它每次选择两个变量进行优化,这两个变量的优化问题是一个带等式和不等式约束条件的二次函数极值问题,可以求出公式解,并且这个问题也是凸优化问题。优化变量的选择通过KKT条件来确定。
相关概念了解
线性可分和线性不可分:
线性可分,在二维空间可以理解为可以用一条直线(一个函数)把两类型的样本隔开,被隔离开来的两类样本即为线性可分样本。同理在高维空间,可以理解为可以被一个曲面(高维函数)隔开的两类样本。
线性不可分,则可以理解为自变量和因变量之间的关系不是线性的。
实际上,线性可不分的情况更多,但是即使是非线性的样本通常也是通过高斯核函数将其映射到高维空间,在高维空间非线性的问题转化为线性可分的问题。
函数间隔和几何间隔:
给定一个训练样本![]() ,x是特征,y是结果标签。i表示第i个样本。我们定义函数间隔如下:
,x是特征,y是结果标签。i表示第i个样本。我们定义函数间隔如下:
![]()
函数间隔代表了特征是正例或是反例的确信度。函数间隔并不能正常反应点到超平面的距离。
当分子成比例的增长时,分母也是成倍增长。为了统一度量,我们需要对法向量w加上约束条件,这样我们就得到了几何间隔γ,几何间隔 geometrical margin定义为:
向量点到超平面的距离![]() (其中
(其中![]() )。几何间隔才是点到超平面的真正距离。
)。几何间隔才是点到超平面的真正距离。
超平面方程 ![]() 的理解:
的理解:
对于二维空间中,我们从初中就开始学习的直线方程形式很简单:
现在让原来的轴变成轴,变成轴,于是上面公式中的直线方程会变成下面的样子:
上面公式的向量形式可以写成:
考虑到我们在等式两边乘上任何实数都不会改变等式的成立,所以我们可以写出一个更加一般的向量表达形式(进一步向量化):
变量略显粗壮,他们是黑体,表示变量是个向量,,,一般我们提到向量的时候,都默认他们是个列向量,所以我在方括号[ ]后面加上了上标T表示转置,它可以帮忙把行向量竖过来变成列向量,所以在公式里面后面的转置符号T,会把列向量又转回到行向量。这样一个行向量和一个列向量就可按照矩阵乘法的方式结合,变成一个标量,然后好跟后面的标量相加后相互抵消变成0。
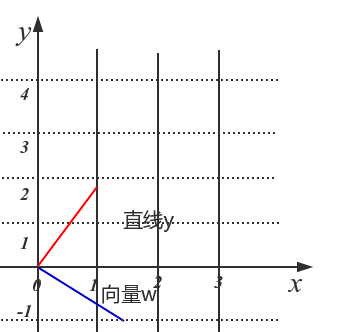
向量和标量的几何意义是什么?对比上面最后两个公式的转化,可以发现此时的。回顾直线方程,还记得那条我们熟悉的直线方程中的a的几何意义吗?对的,那是直线的斜率。如果我们构造一个向量,它应该跟描述的直线平行。然后我们求一下两个向量的点积,你会惊喜地发现结果是0。我们管这种现象叫作“两个向量相互正交”。通俗点说就是两个向量相互垂直。当然,你也可以在草稿纸上自己画出这两个向量,比如让,你会发现在第一象限,与横轴夹角为60°,而在第四象限与横轴夹角为30°,所以很显然他们两者的夹角为90°。
蓝色的线代表向量w,红色的先代表直线y。我们可以看到向量w和直线的关系为垂直关系。这说明了向量w也控制这直线的方向,只不过是与这个直线的方向是垂直的。标量γ的作用也没有变,依然决定了直线的截距。此时,我们称w为直线的法向量。回到决策面方程上来,我们讨论正交或者垂直的目的就是想说明向量跟直线 是相互垂直的,也就是说控制了直线的方向。 是截距,它控制了直线的位置。花了很多篇幅描述一个很简单的超平面方程(其实只是个直线方程),这里真正有价值的是这个控制方向的参数。接下来,你会有很长一段时间要思考它到底是个什么东西,对于SVM产生了怎样的影响。
推广到n维空间,就变成了超平面方程:
公式没变,不同之处在于:
分类间隔方程的理解(几何间隔才是svm点到超平面的真正距离):
依然对于一个二维平面的简单例子进行推导。间隔的大小实际上就是支持向量对应的样本点到决策面的距离的二倍。
我们已经知道间隔的大小实际上就是支持向量对应的样本点到决策面的距离的二倍。那么图中的距离d我们怎么求?我们高中都学过,点到直线的距离距离公式如下:
现在,将直线方程扩展到多维,求得我们现在的超平面方程,对公式进行如下变形:
这个d就是分类间隔。其中||w||表示w的二范数,求所有元素的平方和,然后再开方。比如对于二维平面:
相当于:
也可以说这里的是向量的模,表示在空间中向量的长度,就是支持向量样本点的坐标。就是决策面方程的参数。而追求的最大化也就是寻找的最大化。看起来我们已经找到了目标函数的数学形式。为了找出一个分类效果好的超平面作为分类器。分类器的好坏的评定依据是分类间隔W=2d的大小,即分类间隔W越大,我们认为这个超平面的分类效果越好。此时,求解超平面的问题就变成了求解分类间隔W最大化的为题。W的最大化也就是d最大化的。
理解上面的内容之后,再看下文。
线性SVM算法的数学建模:
一个最优化问题通常有两个最基本的因素:1)目标函数,也就是你希望什么东西的什么指标达到最好;2)优化对象,你期望通过改变哪些因素来使你的目标函数达到最优。在线性SVM算法中,目标函数显然就是那个“分类间隔”,而优化对象则是决策面。所以要对SVM问题进行数学建模,首先要对上述两个对象(“分类间隔”和“决策面”)进行数学描述。
在分离超平面固定为,则||表示点x到超平面的相对距离。通过观察 和 是否同号,我们判断分类是否正确。所以函数间隔定义为:
而函数间隔不能正常反应点到超平面的距离,因为当我们等比例扩大和的时候,函数间隔也会扩大相应的倍数。因此,我们引入几何间隔。几何间隔就是在函数间隔的基础下,在分母上对加上约束(这个约束有点像归一化),定义为:
不过这里的![]() 是带符号的,我们需要的只是它的绝对值,因此类似地,也乘上对应的类别y(一般取+1和-1)即可,因此实际上我们定义几何间隔:
是带符号的,我们需要的只是它的绝对值,因此类似地,也乘上对应的类别y(一般取+1和-1)即可,因此实际上我们定义几何间隔:
当其类标记为yi=-1,点A与超平面的距离记作di,那么:
所以点xi与超平面的距离是:
所以超平面关于样本点xi的几何间隔实际上就是点到平面距离:
SVM模型目标函数与优化
根据SVM的思想,我们可以知道是要取最大化支持向量到超平面的几何间隔,用数学式子表示为:
一般我们都取函数间隔γ′=1γ′=1,这样我们的优化函数定义为:
最大化 ,也就等价于最小化 ( 是为了后面求导以后形式简洁,不影响结果),因此SVM模型的求解最大分割超平面问题又可以表示为以下约束最优化问题:
这就是支持向量机的基本模型。这里m是样本点的总个数,缩写s.t.表示”Subject to”,是”服从某某条件”的意思。上述公式描述的是一个典型的不等式约束条件下的二次型函数优化问题,同时也是支持向量机的基本数学模型。由目标函数是二次的,而约束条件是线性的,所以它是一个凸二次规划问题。SVM的数学模型即是:不等式约束条件下的二次型函数优化,而求解这一类优化问题,接下来我们需要构造拉格朗乘子函数。总之一句话:在一定的约束条件下,目标最优,损失最小。
解这一类优化问题之前,先来了解几个概念:
凸函数:
在凸集中任取两个点连成一条直线,这条直线上的点仍然在这个集合内部,左边凸函数局部最优就是全局最优,而右边的非凸函数的局部最优就不是全局最优了。
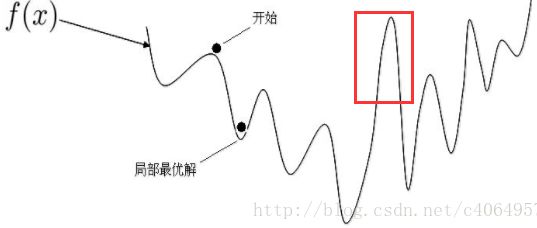
再看一幅图如下,它整体就是一个非凸函数,我们无法获得全局最优解的,只能获得局部最优解。比如红框内的部分,如果单独拿出来,它就是一个凸函数。
对于我们的目标函数,很显然它是一个凸函数。
通常我们需要求解的最优化问题有如下几类:
1. 无约束优化问题:对于这类的优化问题,使用的方法就是费马大定理(Fermat),即求取函数f(x)的导数,然后令其为零,可以求得候选最优值,再在这些候选值中验证;如果是凸函数,可以保证是最优解。这也就是我们高中经常使用的直接求函数的极值的方法。可以写为:
2. 有等式约束的优化问题:对于这类的优化问题,使用的方法就是拉格朗日乘子法(Lagrange Multiplier) ,即把等式约束h_i(x)用一个系数与f(x)写为一个式子,称为拉格朗日函数,而系数称为拉格朗日乘子。通过拉格朗日函数对各个变量求导,令其为零,可以求得候选值集合,然后验证求得最优值。可以写为:
3. 有不等式约束的优化问题:对于这类的优化问题,使用的方法就是KKT条件。同样地,我们把所有的等式、不等式约束与f(x)写为一个式子,也叫拉格朗日函数,系数也称拉格朗日乘子,通过一些条件,可以求出最优值的必要条件,这个条件称为KKT条件。可以写为:
必要条件和充要条件如果不理解,可以看下面这句话:A的必要条件就是A可以推出的结论;A的充分条件就是可以推出A的前提。
拉格朗日函数:
拉格朗函数的目的,就是将约束条件融合到目标函数中,构造一个新函数来表示目标函数,将有约束的优化问题转化为无约束的优化问题。我们知道我们要求解的是最小化问题,所以一个直观的想法是如果我能够构造一个函数,使得该函数在可行解区域内与原目标函数完全一致,而在可行解区域外的数值非常大,甚至是无穷大,那么这个没有约束条件的新目标函数的优化问题就与原来有约束条件的原始目标函数的优化问题是等价的问题。这就是使用拉格朗日方程的目的,它将约束条件放到目标函数中,从而将有约束优化问题转换为无约束优化问题。
首先定义原始目标函数,拉格朗日乘子法的基本思想是把约束条件转化为新的目标函数的一部分,从而使有约束优化问题变成我们习惯的无约束优化问题。那么该如何去改造原来的目标函数使得新的目标函数的最优解恰好就在可行解区域中呢?这需要我们去分析可行解区域中最优解的特点。构造一个拉格朗日函数,将有约束优化问题转为无约束优化问题。拉格朗日函数具体形式如下:
![]()
根据我们熟悉的求解无约束优化问题的思路,将上面公式分别对求导,令结果等于零,就可以建立两个方程。随后,人们又发现,使用拉格朗日获得的函数,使用求导的方法求解依然困难。进而,需要对问题再进行一次转换,即使用一个数学技巧:拉格朗日对偶。
按照前面等式约束条件下的优化问题的求解思路,构造拉格朗日方程的目的是将约束条件放到目标函数中,从而将有约束优化问题转换为无约束优化问题。我们仍然秉承这一思路去解决不等式约束条件下的优化问题,那么如何针对不等式约束条件下的优化问题构建拉格朗日函数呢?
因为我们要求解的是最小化问题,所以一个直观的想法是如果我能够构造一个函数,使得该函数在可行解区域内与原目标函数完全一致,而在可行解区域外的数值非常大,甚至是无穷大,那么这个没有约束条件的新目标函数的优化问题就与原来有约束条件的原始目标函数的优化是等价的问题。
拉格朗日对偶问题其实就是沿着这一思路往下走的过程中,为了方便求解而使用的一种技巧。于是在这里出现了三个问题:1)有约束的原始目标函数优化问题;2)新构造的拉格朗日目标函数优化问题;3)拉格朗日对偶函数的优化问题。我们希望的是这三个问题具有完全相同的最优解,而在数学技巧上通常第三个问题——拉格朗日对偶优化问题——最好解决。所以拉格朗日对偶不是必须的,只是一条捷径。
所以,显而易见的是,我们在拉格朗日优化我们的问题这个道路上,需要进行下面二个步骤:
- 将有约束的原始目标函数转换为无约束的新构造的拉格朗日目标函数
- 使用拉格朗日对偶性,将不易求解的优化问题转化为易求解的优化
下面,进行第一步:将有约束的原始目标函数转换为无约束的新构造的拉格朗日目标函数:
其中αi是拉格朗日乘子,每一个约束条件对应一个拉格朗日乘子,αi大于等于0,构造新目标函数时引入的系数变量(我们自己设置)。原优化问题可以转化为(求拉格朗函数的最大值):
讨论如下条件(1)(2):
(1) 当样本点不满足约束条件时,即说明在可行解区域外:![]() ,此时将αi置为正无穷大,那么θ(w)显然也是正无穷大;
,此时将αi置为正无穷大,那么θ(w)显然也是正无穷大;
(2) 当样本点满足约束条件时,即说明在可行解区域内:![]() ,可行解区域内,此时θ(w)的最小值就是原目标函数。
,可行解区域内,此时θ(w)的最小值就是原目标函数。
于是综上所述,引入拉格朗乘子函数后,可以得到新的目标函数:
此时,再看我们的初衷,就是为了建立一个在可行解区域内与原目标函数相同,在可行解区域外函数值趋近于无穷大的新函数,现在我们的问题变成了求新目标函数的最小值。实际上等价于直接最小化θ(w)(当然,这里也有约束条件,就是αi≥0,i=1,…,n)αi≥0,i=1,…,n),因为如果约束条件没有得到满足,θ(w)会等于无穷大,自然不会是我们所要求的最小值。
此时θ(w)的最小值就是原目标函数,于是综上所述,引入拉格朗乘子函数后,可以得到新的目标函数:
我们用p*表示优化目标函数后的最优解,且与最初的目标函数等价。
我们看一下我们的新目标函数,先求最大值,再求最小值。这样的话,我们首先就要面对带有需要求解的参数w和b的方程,而αi又是不等式约束,这个求解过程不好做。所以,我们需要使用拉格朗日函数对偶性,将最小和最大的位置交换一下,这样就变成了:
这就是线性可分条件下支持向量机的对偶算法。这样做的优点在于:一是原问题的对偶问题往往更容易求解,二者可以自然的引入核函数,进而推广到非线性分类问题。从上式中,我们可以先求目标函数对于和的极小值,再求拉格朗日乘子的极大值。
上式变化使用了拉格朗日函数的对偶性,交换以后的新问题是原始问题的对偶问题,这个新问题的最优值用d*来表示,d*的求导过程比p*相对容易,而且d*<=p*。我们关心的是d=p的时候,这才是我们要的解。需要什么条件才能让d=p呢?
- 首先必须满足这个优化问题是凸优化问题。
- 其次,最优值需要满足KKT条件。
凸优化问题的定义是:求取最小值的目标函数为凸函数的一类优化问题。目标函数是凸函数我们已经知道,这个优化问题又是求最小值。所以我们的最优化问题就是凸优化问题。
接下里,就是探讨是否满足KKT条件了。
KKT条件的描述:(KKT条件是对最优解的约束,而原始问题中的约束条件是对可行解的约束)
我们已经使用拉格朗日函数对我们的目标函数进行了处理,生成了一个新的目标函数。通过一些条件,可以求出最优值的必要条件,这个条件就是接下来要说的KKT条件。一个最优化模型能够表示成下列标准形式:

其中f(x)是需要最小化的函数,h(x)是等式约束,g(x)是不等式约束,m和n分别是等式约束和不等式约束的数量。KKT条件的全称是Karush-Kuhn-Tucker条件,KKT条件即是规定f(x)的最优值必须满足以下(1)(2)(3)条件,只有满足KKT条件,目标函数的最优化问题依然可以用拉格朗日乘子法解决。
- 条件一:经过拉格朗日函数处理之后的新目标函数L(w,b,α)对α求导为零:
- 条件二:h(x) = 0;
- 条件三:α*g(x) = 0;
拉格朗日对偶参考博客:https://www.cnblogs.com/jerrylead/archive/2011/03/13/1982684.html
求解对偶问题:
上面分析了目标函数满足凸优化和KKT条件,则问题转化为求解原问题的对偶问题(即p*=d*)。而求解这个对偶学习问题,可以分为三个步骤:首先要让L(w,b,α)关于w和b最小化,然后求对α的极大,最后利用SMO算法求解对偶问题中的拉格朗日乘子。
1)、首先固定α, 要让L(w,b,α)关于w和b最小化 ,关于 w 和 b 最小化,我们分别对w,b求偏导数,即令 ∂L/∂w 和 ∂L/∂b 等于零:从上两式子可以看出,我们已经求得了w和α的关系,只要我们后面接着能够求出优化函数极大化对应的α,就可以求出我们的w了,至于b,由于上两式已经没有b,所以最后的b可以有多个。好了,既然我们已经求出w和α的关系,就可以带入优化函数L(w,b,α)消去w,将上述结果带回L(w,b,α)得到(推导过程略):
2)求对α的极大,即是关于对偶问题的最优化问题(内侧的最小值求解完成,我们求解外侧的最大值)。经过上面第一个步骤的求w和b,得到的拉格朗日函数式子已经没有了变量w,b,只有α。从上面的式子得到对α求极大化的数学表达式最终如下:
只要我们可以求出上式极小化时对应的α向量就可以求出w和b了,进而求得我们最初的目的:找到超平面,即”决策平面”和分类决策函数。具体怎么极小化上式得到对应的α,一般需要用到SMO(序列最小优化)算法,这个算法比较复杂(待总结)。在这里,我们假设通过SMO算法,我们得到了对应的α的值α∗:那么可以求出w:
再求 :
求得分离超平面:
分类决策函数:
到这里线性可分SVM学习差不多了。
当然线性可分SVM方法对于非线性的数据集是没有办法使用的, 有时候不能线性可分的原因是线性数据集里面多了少量的异常点,由于这些异常点导致了数据集不能线性可分, 那么怎么可以处理这些异常点使数据集依然可以用线性可分的思想呢? 涉及到线性SVM的软间隔最大化(未完待续)
# 线性支持向量机以及软间隔最大化(待总结)
# 线性不可分SVM与核函数(待总结)
参考文章:
刘建平pinard:https://www.cnblogs.com/pinard/p/6097604.html
人工智站:https://www.cnblogs.com/huangyc/p/9931233.html
支持向量机原理篇之手撕线性SVM:https://blog.csdn.net/c406495762/article/details/78072313
支持向量机通俗导论(理解SVM的三层境界):https://blog.csdn.net/iluckyflower/article/details/16881137
深入理解SVM+初始:https://blog.csdn.net/sinat_35512245/article/details/54984251
JerryLead:https://www.cnblogs.com/jerrylead/archive/2011/03/18/1988419.html
svm测试题:https://www.jianshu.com/p/c23214a6bb09