AC自动机

一直想写AC自动机了
但是考虑到学习AC自动机之前
还需要一点其他的知识的基础
于是我先补充好了Trie树和KMP的blog
如果以上两个知识点没有学好的话
请先学习这两个知识点再来学习AC自动机
Trie（字典树）
KMP算法

---

如果能够解决上面的两个 算法/结构 那么，
欢迎继续学习AC自动机

首先我们要知道AC自动机是干什么用的。

大家都知道KMP算法是求单字符串对单字符串的匹配使用的
（因为我默认你们上面的两个东西都学好了）

那么，多个字符串在一个字符串上的匹配怎么办？

---

举例子永远是最好的

求 abab 在 abababbabbaabbabbab 中出现了几次
很明显，求出abab的next数组，然后进行KMP的匹配即可出解。

2. 求 aba aca bab sab sba 在字符串 asabbasbaabbabbacaacbscbs 中总共出现了几次。 嗯嗯嗯。。。 这个要怎么办？ 每次对一个需要匹配的串求一次next数组，然后一次次去匹配？ 显然，这样变得很慢很慢了。。。 如果需要匹配的串很多很多的话。。。。。 不敢想象。。，，

---

那么，我们要如何解决这类问题呢？
恩，AC自动机。

常规而言，看看AC自动机是啥玩意
以下来自某度某科：
Aho-Corasick automation，该算法在1975年产生于贝尔实验室，是著名的多模匹配算法。

好吧，这个说了跟没说似的（就象征意义的看一下吧）

---

正式开始，我们来讲解AC自动机

AC自动机需要提前知道所有的需要匹配的字符串
例如
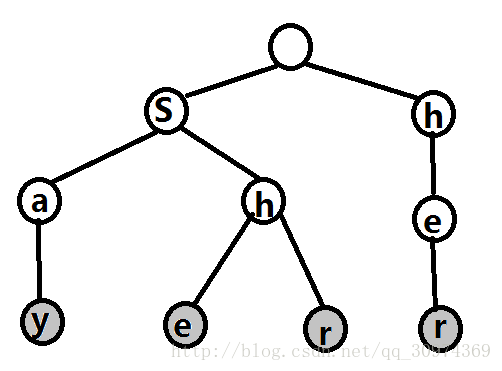
say she shr her

---

那么第一步
把它们构建成一棵Trie树

灰色的结点代表一个单词的结尾

第一步应该是最简单的一步之一
只需要构建一棵Trie树即可
（再说一遍，如果前面两个东西没学好，先去学习完再继续学习AC自动机）

---

接着是第二步，也就是最重要的一步。
构建失配指针

这一步很KMP算法中的next数组是类似的，通过跳转来省略重复的检查。

那么要如何构建呢？

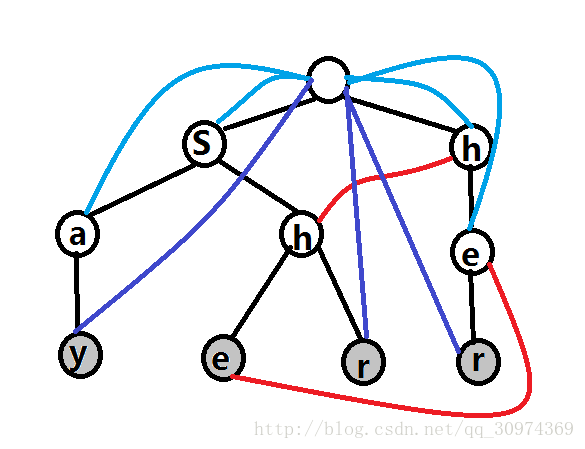
我先把构建好的放出来。

恩恩

我知道我画的图很丑很丑很丑

并不要在意那些奇怪的颜色问题

虽然画在了这里，，，，但是
并不知道怎么求对不对。。
我们先看看这个指针是要干什么吧。
每次沿着Trie树匹配，匹配到当前位置没有匹配上时，直接跳转到失配指针所指向的位置继续进行匹配。

所以，这个Trie树的失配指针要怎么求？

dalao们的blog告诉我们

Trie树的失配指针是指向：沿着其父节点 的 失配指针，一直向上，直到找到拥有当前这个字母的子节点 的节点 的那个子节点

感觉听起来很复杂吧。。。。

我也是这么觉得的

但是
自己画一下图就好了

值得一提的是，第二层的所有节点的失配指针，都要直接指向Trie树的根节点。

---

我也觉得我自己讲的很复杂。。。。。

怎么说呢，求失配指针是一个BFS的过程
需要逐层扩展（因为要用到父节点的失配指针）

所以，觉得每一次求失配指针都需要沿着之前的失配指针走一遍？

显然并不需要

那么怎么办？

这里看代码，自己理解一下（画图就是学习AC自动机的诀窍）

void Get_fail()//构造fail指针
{
	    queue Q;//队列 
	    for(int i=0;i<26;++i)//第二层的fail指针提前处理一下
        {
        	   if(AC[0].vis[i]!=0)
        	   {
        	       AC[AC[0].vis[i]].fail=0;//指向根节点
				   Q.push(AC[0].vis[i]);//压入队列 
			   }
	    }
	    while(!Q.empty())//BFS求fail指针 
	    {
	    	  int u=Q.front();
	    	  Q.pop();
			  for(int i=0;i<26;++i)//枚举所有子节点
			  {
			  	      if(AC[u].vis[i]!=0)//存在这个子节点
					  {
					  	           AC[AC[u].vis[i]].fail=AC[AC[u].fail].vis[i];
					  	          //子节点的fail指针指向当前节点的
								  //fail指针所指向的节点的相同子节点 
					  	      Q.push(AC[u].vis[i]);//压入队列 
					  }
					  else//不存在这个子节点 
					  AC[u].vis[i]=AC[AC[u].fail].vis[i];
					  //当前节点的这个子节点指向当
					  //前节点fail指针的这个子节点 
		      }
	    }
}

如果你仔细的画画图
就会发现上面是一种很巧妙的构建方式
并不需要沿着失配指针向上移动。

---

嗷。。。。
失配指针写完了。。。
最后直接写匹配？？？
这个我觉得没有必要贴代码
直接讲述一下即可

首先，指针指向根节点
依次读入单词，检查是否存在这个子节点
然后指针跳转到子节点
如果不存在
直接跳转到失配指针即可

---

AC自动机差不多就到这里
三个模板题我放一下链接，大家可以自己查阅一下完整代码

【洛谷3808】
【洛谷3796】
【CJOJ1435】

---

upd:2018.3.28

啊，这篇文章是去年暑假写的
我果断的更新一下。

重新描述一下关于\(fail\)指针的理解
\(fail\)是失配指针，注意是失配
意味着，如果我此时匹配失败，那么，我们就要到达这个指针指向的位置继续常数匹配
所以，我们可以将失配指针指向的的节点理解为：
当前节点所代表的串，最长的、能与后缀匹配的，在\(Trie\)中出现过的前缀所代表的节点。
所以，\(fail\)指针类似于\(kmp\)的\(next\)数组，只不过由单串变为了多串而已。

---

我们很明显的看到之前的构建方法是把\(Trie\)树补全，变成了\(Trie\)图
虽然很好写，但并不是试用所有情况下，有的时候需要保留原来的\(Trie\)树的结构
此时就需要沿着\(fail\)进行寻找学完回文树之后对这类玩意有感觉多了
所以，我重新提供一个真正的\(AC\)自动机的代码
这份代码因为转移试用了\(map\)记录，因此有一些\(STL\)的操作

void BuildFail()
{
	queue Q;
	for(it=t[0].son.begin();it!=t[0].son.end();++it)Q.push(it->second);
	while(!Q.empty())
	{
		int u=Q.front();Q.pop();
		if(!t[u].son.size())continue;
		for(it=t[u].son.begin();it!=t[u].son.end();++it)
		{
			int v=it->second,c=it->first,p=t[u].ff;
			while(p&&!t[p].son[c])p=t[p].ff;
			if(t[p].son[c])t[v].ff=t[p].son[c];
			Q.push(v);
			t[v].fl|=t[t[v].ff].fl;
		}
	}
}