北航软工结对项目作业
一,作业信息
| 项目 | 内容 |
|---|---|
| 这个作业属于哪个课程 | 2020春季计算机学院软件工程(罗杰 任健) |
| 这个作业的要求在哪里 | 结对项目作业 |
| 我在这个课程的目标是 | 学习软件工程相关知识,提高自己团队项目的开发能力 |
| 教学班级 | 005 |
| 项目地址 | PairIntersectProject |
二,PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 120 | 120 |
| · Estimate | · 估计这个任务需要多少时间 | ||
| Development | 开发 | ||
| · Analysis | · 需求分析 (包括学习新技术) | 180 | 300 |
| · Design Spec | · 生成设计文档 | 60 | 30 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 30 | 15 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 30 | 15 |
| · Design | · 具体设计 | 120 | 120 |
| · Coding | · 具体编码 | 240 | 300 |
| · Code Review | · 代码复审 | 30 | 30 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 60 | 90 |
| Reporting | 报告 | ||
| · Test Report | · 测试报告 | 30 | 20 |
| · Size Measurement | · 计算工作量 | 10 | 10 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 30 | 30 |
| 合计 | 870 | 1080 |
三,看教科书和其它资料中关于 Information Hiding,Interface Design,Loose Coupling 的章节,说明你们在结对编程中是如何利用这些方法对接口进行设计的
Information Hiding:
- 遵循信息隐藏原则是优秀的模块设计的必要条件,信息隐藏的意思是仅仅向外界暴露他们必须要知道的东西,至于内部的数据结构,算法等实现机制则完全隐藏,这一原则在这次作业的接口设计中体现的尤为明显。软件类接口本身的定位就是向外界提供某种功能,当调用接口时只需关注其用法而忽略其实现机制。以这次作业为例,我们将任务分为UI编写者和接口提供者,那么接口提供者就应该在了解UI端所需要支持的操作后,将源程序功能进行规划封装,最后以dll文件形式向UI端提供其需要的接口。而UI编写者只需要在项目中引用dll,根据相应接口规范使用接口即可,所有需要的功能都是封装好的,不需要对源程序内部数据结构或算法有其他了解,如此一来项目团队的工作层次就会清晰许多,若出现Bug也能快速定位相应模块,提高工作效率。除此之外,在类的定义中也体现着信息隐藏,我们通常会对类属性加以private声明,并提供相应的方法来外界来访问属性值,从这里可以看出信息隐藏原则对于程序的安全性也有相当的保证。
Interface Design:
- 接口设计是实现信息隐藏原则以及程序模块化设计的重要工具,优秀的接口设计可以使程序结构井然有序,大大提升开发效率,而糟糕的接口设计却可能适得其反。我们在这次作业中设计接口时尽量遵循最小化原则,一方面,在参数能满足要求的前提下尽可能减少参数个数,当然,无用的参数是必须要舍弃的,但有时为了未来程序的可扩展性考虑也可能多留一些参数,这需要设计师自己的来权衡;另一方面,接口提供的功能应尽量专一,一个内容繁杂的接口虽然可能功能强大,但在可维护性以及可用性上可能会大打折扣,不如设计小而精的接口,提升开发效率。
Loose Coupling:
- 耦合表示两个功能函数之间的依赖程度,松耦合即要求我们设计的各功能函数之间的依赖程度不要太高。否则,在我们修改完一个函数后,可能还需要对依赖于它的那些函数做出修改,在这次作业中,我们设计了很多功能单一的功能函数,例如对直线类和圆类初始化,特定几何对象之间的交点求解等,尽可能将功能细化使得他们之间的依赖程序降低,此外,将计算模块封装成core后,也实现了计算模块与界面设计模块之间的松耦合。
四,计算模块接口的设计与实现过程。设计包括代码如何组织,比如会有几个类,几个函数,他们之间关系如何,关键函数是否需要画出流程图?说明你的算法的关键(不必列出源代码),以及独到之处
对于本次作业的新增需求,我们通过对直线类进行扩展来实现,用type属性表示相应的直线类型:
- L:表示直线,其交点求解没有范围限制
- R:表示射线,其交点求解范围受左端点的限制
- S:表示线段,其交点求解范围受两边端点的限制
接口模块共有一个类两个函数:
- class Point:点类,用于存储交点
- get_inters(5参数):求线类与已有几何图形的交点
- get_inters(3参数):求圆与已有几何图形的交点
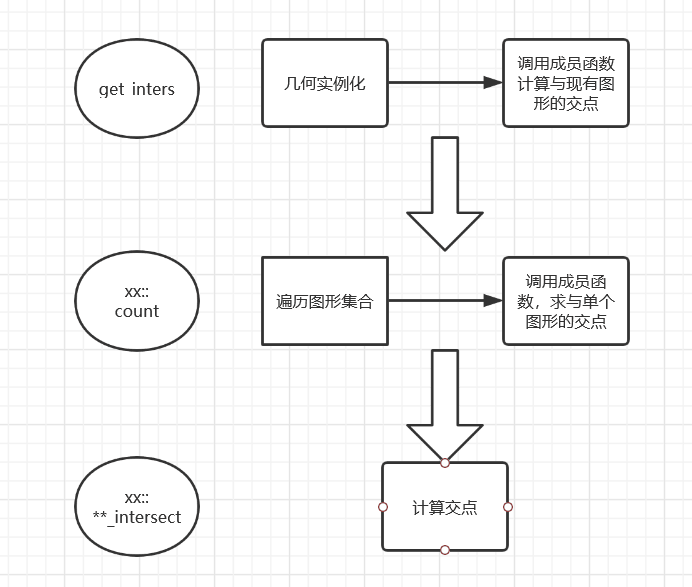
函数的动作流程如下图所示:
我们这一接口的关键之处在于彻底隐藏了求解交点内部的数据结构组织,调用者在使用接口求解交点时,甚至不需要了解Line和Circle类,直接输入相应几何对象的描述就可以返回该几何对象与目前所有在容器中的几何对象的交点。
五,阅读有关 UML 的内容,画出 UML 图显示计算模块部分各个实体之间的关系(画一个图即可)
我们用Geometry来表示几何对象类,具体的几何对象则分为Line类和Circle类,除此之外用Point类来记录交点信息。
六,计算模块接口部分的性能改进。记录在改进计算模块性能上所花费的时间,描述你改进的思路,并展示一张性能分析图,并展示你程序中消耗最大的函数
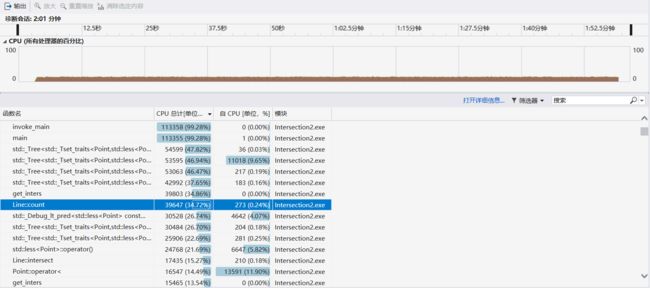
性能分析如下图所示:
从该性能分析图中可以看出,set的查找和排序占据大量的CPU资源,对于此我认为实用unordered_set会改善性能,因为其查找效率更高一点,但是我们本次作业并没有进行此项改进,只对计算交点的算法进行了改进。不同于上次作业的用公式求,本次作业采用向量法求解交点,改进了计算的效率。
七,看 Design by Contract,Code Contract 的内容,描述这些做法的优缺点,说明你是如何把它们融入结对作业中的
契约式设计是一种设计计算机软件的方法。这种方法要求软件设计者为软件组件定义正式的,精确的并且可验证的接口,这样,为传统的抽象数据类型又增加了先验条件、后验条件和不变式。
- 先验条件:为了调用函数,必须为真的条件,在其违反时,函数决不调用,传递好数据是调用者的责任
- 后验条件:函数保证能做到的事情,函数完成时的状态,函数有这一事实表示它会结束,不会无休止的循环
- 不变式:从调用者的角度来看,该条件总是为真,在函数的内部处理过程中,不变项可以为变,但在函数结束后,控制返回调用者时,不变项必须为真
优点:
- 契约式设计鼓励程序员思考诸如“例程的先验条件是什么”这样的问题,这样有助于程序员理清概念,获得更优秀的设计
- 编写契约可以帮助开发者更好地理解代码,且可以提高开发测试的效率,提高项目可靠性
- 契约可以带来高质量的文档,例如运行时要检查断言,以保证制定的契约与程序的实际运行情况一致,出色的开发文档对于团队是十分重要的
缺点:
- 契约式设计需要大量时间学习撰写良好的契约,这样才能达到其效果
- 用于进行程序正确性检验上的时间精力也是巨大的,需要大量投入
- 有些项目不适合使用契约式设计,可能会延缓进度,适得其反
在这次作业中,契约设计可以帮助我们提高程序的正确性以及规范性,比如在错误处理中,我们可以用一些约束条件对输入数据的有效性进行限制,但这次作业中我们对很多工具的使用都有生疏不足之处,常常需要对之前制定好的设计进行修改,我认为本次作业我们没有依赖于契约式设计。
八,计算模块部分单元测试展示。展示出项目部分单元测试代码,并说明测试的函数,构造测试数据的思路
接口函数是软件的最顶级函数,其功能为求出图形与已经记录的图形的交点,每个类型的对象都进行测试:
- 当前线对象求与线的交点
- 当前线对象求与圆的交点
- 当前圆对象求与线的交点
- 当前圆对象求与圆的交点
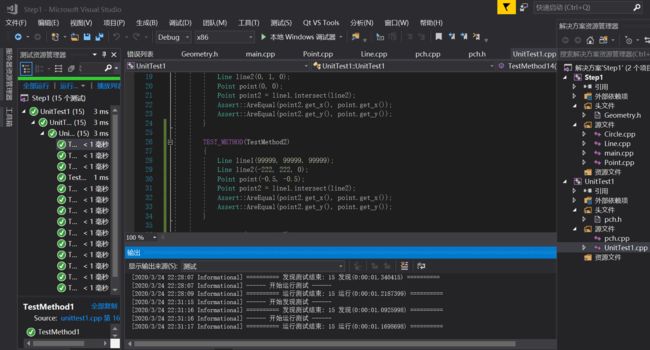
如下展示测试两直线交点的单元测试代码:
TEST_METHOD(TestMethod1)
{
Line line1(1, -1, 0);
Line line2(0, 1, 0);
Point point(0, 0);
Point point2 = line1.intersect(line2);
Assert::AreEqual(point2.get_x(), point.get_x());
Assert::AreEqual(point2.get_y(), point.get_y());
}
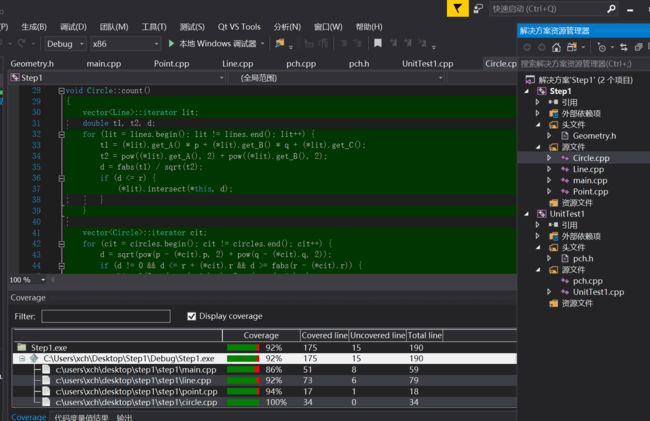
测试覆盖率展示:
九,计算模块部分异常处理说明。在博客中详细介绍每种异常的设计目标。每种异常都要选择一个单元测试样例发布在博客中,并指明错误对应的场景
| 错误类型 | 输入(其中一种) | 输出 |
|---|---|---|
| 圆半径非正 | C 0 0 0 | R should > 0! |
| 类型未定义 | a 0 0 1 | Undefined type! |
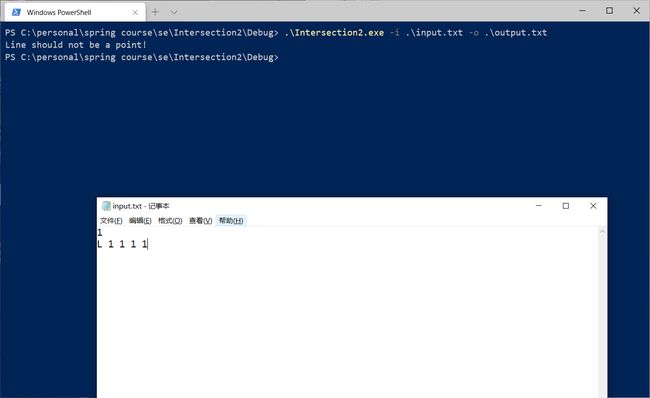
| 线类两点重合 | L 1 1 1 1 | Line should be a point! |
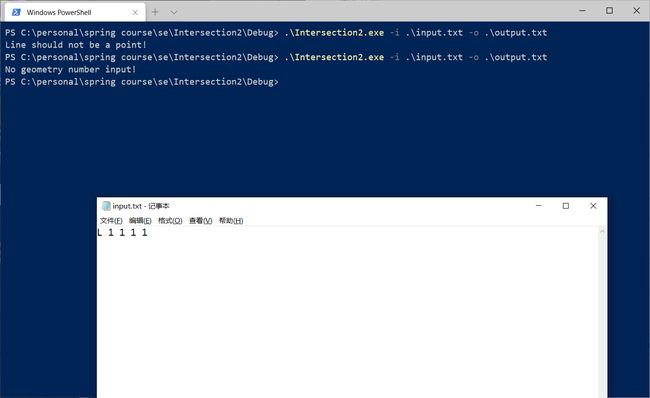
| 未指明输入的几何对象数目 | - | No geometry number input! |
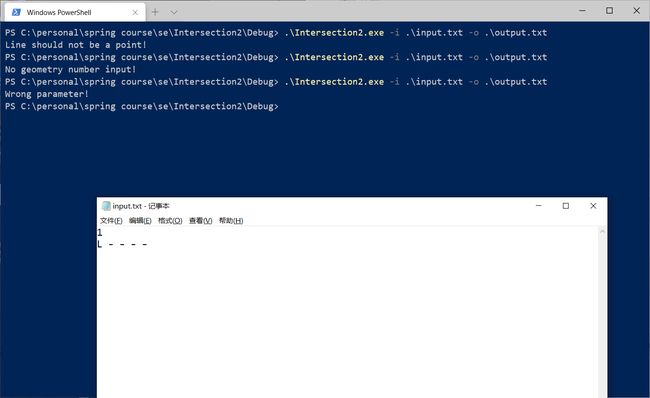
| 参数错误 | L - - - - | Wrong parameter! |
- 圆半径非正
- 未定义的几何对象类型
- 直线定义两点重合
- 未指明输入的几何对象数目
- 参数错误
十,界面模块的详细设计过程。在博客中详细介绍界面模块是如何设计的,并写一些必要的代码说明解释实现过程
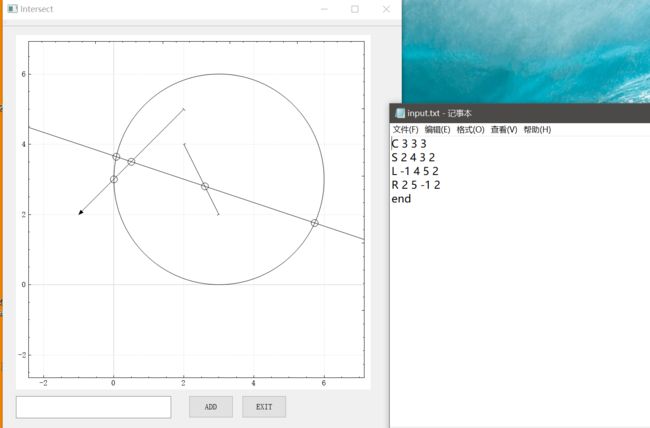
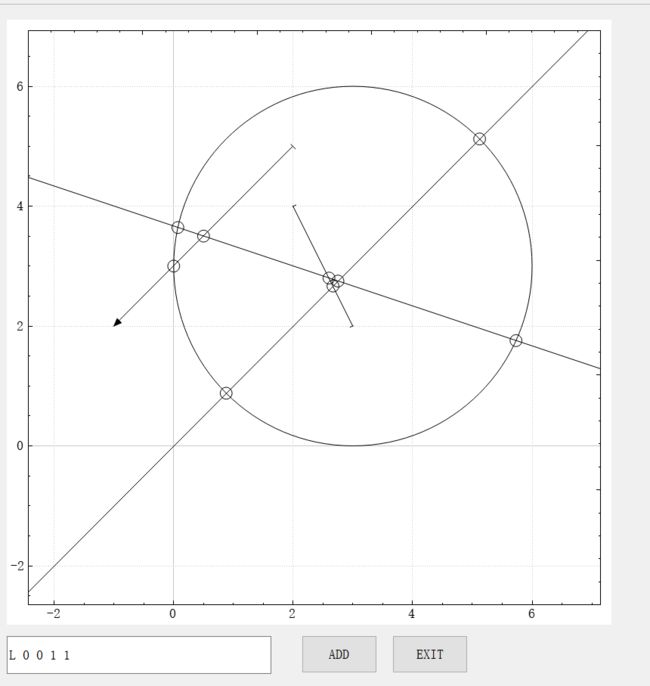
本次UI设计使用QT进行设计,本来打算使用基本的widget进行设计,后来了解到QCustomPlot对于界面的放大,缩小,移动等操作都有很好的支持,故引入QCustomPlot库进行设计,主界面如图所示:
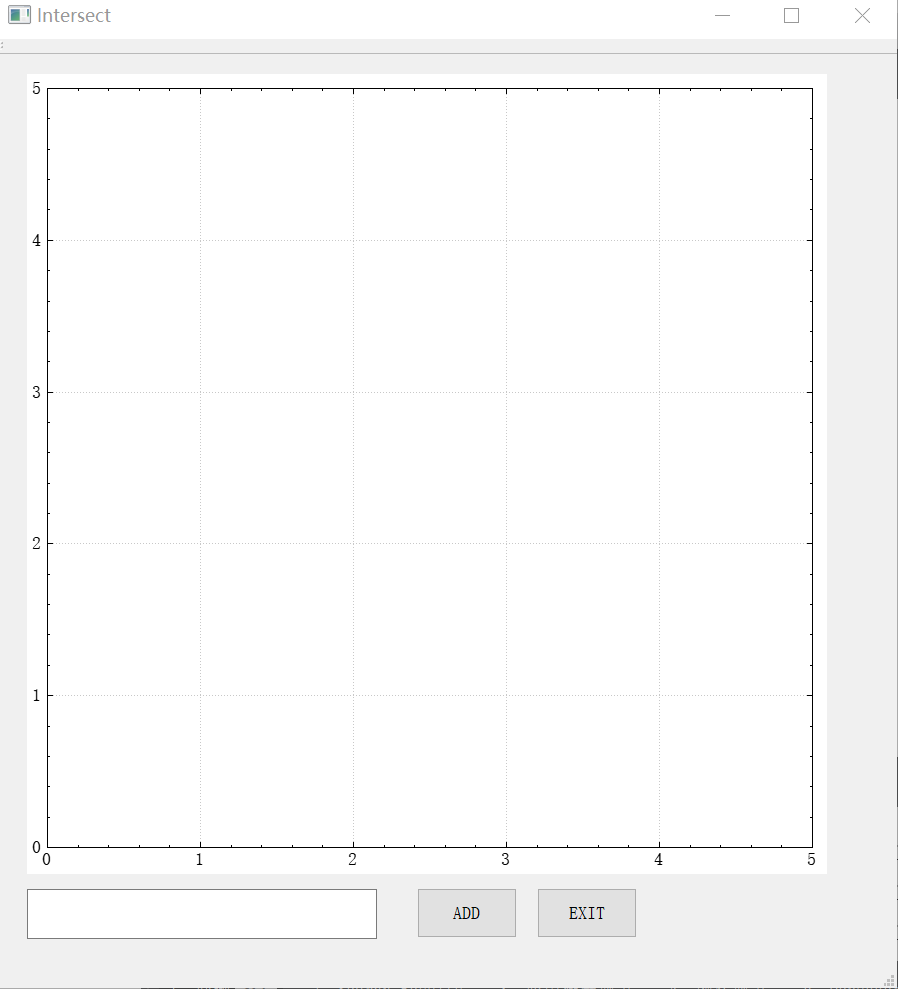
- QCustomPlot绘图环境:
ui->widget->addGraph(0);
ui->widget->axisRect()->setupFullAxesBox();
ui->widget->xAxis->setScaleRatio(ui->widget->yAxis,1.0);
ui->widget->xAxis2->setScaleRatio(ui->widget->yAxis2,1.0);
ui->widget->rescaleAxes();
ui->widget->setInteractions(QCP::iRangeDrag | QCP::iRangeZoom | QCP::iSelectPlottables);
connect(btn1, &QPushButton::clicked, this, &MainWindow::getdate);
connect(btn2, &QPushButton::clicked, this, &MainWindow::close);
- 定义按钮
//按钮
QPushButton * btn1 = new QPushButton("ADD", this);
btn1->setParent(this);
btn1->move(420,850);
btn1->resize(100, 50);
QPushButton * btn2 = new QPushButton("EXIT", this);
btn2->setParent(this);
btn2->move(540,850);
btn2->resize(100, 50);
- 定义获取数据的信号槽
connect(btn1, &QPushButton::clicked, this, &MainWindow::getdate);
void MainWindow::getdate(){
QString name = ui->lineEdit->text();
int i = 0;
string s = name.toStdString();
if (s[0] == 'C'){
double p ,q, r;
i = 2;
string num = "";
while(s[i] != ' '){
num = num + s[i];
i++;
}
i++;
p = atoi(num.c_str());
num = "";
while(s[i] != ' '){
num = num + s[i];
i++;
}
i++;
q = atoi(num.c_str());
num = "";
while(s[i] != '\0'){
num = num + s[i];
i++;
}
r = atoi(num.c_str());
QCPItemEllipse *circle = new QCPItemEllipse(ui->widget);
circle->topLeft->setType(QCPItemPosition::PositionType::ptPlotCoords);
circle->bottomRight->setType(QCPItemPosition::PositionType::ptPlotCoords);
circle->topLeft->setCoords(p-r,q-r);
circle->bottomRight->setCoords(p+r,q+r);
sss = get_inters(p,q,r);
set::iterator iter = sss.begin();
while (iter!=sss.end())
{
QCPItemEllipse *circle = new QCPItemEllipse(ui->widget);
circle->topLeft->setType(QCPItemPosition::PositionType::ptPlotCoords);
circle->bottomRight->setType(QCPItemPosition::PositionType::ptPlotCoords);
circle->topLeft->setCoords( (*iter).x-0.1,(*iter).y-0.1);
circle->bottomRight->setCoords((*iter).x+0.1,(*iter).y+0.1);
iter++;
}
}
if (s[0] == 'L'){
double x1 ,y1, x2, y2;
i = 2;
string num = "";
while(s[i] != ' '){
num = num + s[i];
i++;
}
i++;
x1 = atoi(num.c_str());
num = "";
while(s[i] != ' '){
num = num + s[i];
i++;
}
i++;
y1 = atoi(num.c_str());
num = "";
while(s[i] != ' '){
num = num + s[i];
i++;
}
i++;
x2 = atoi(num.c_str());
num = "";
while(s[i] != '\0'){
num = num + s[i];
i++;
}
y2 = atoi(num.c_str());
QCPItemStraightLine *line = new QCPItemStraightLine(ui->widget);
line->point1->setType(QCPItemPosition::PositionType::ptPlotCoords);
line->point2->setType(QCPItemPosition::PositionType::ptPlotCoords);
line->point1->setCoords(x1,y1);
line->point2->setCoords(x2,y2);
sss = get_inters('L',x1,y1,x2,y2);
set::iterator iter = sss.begin();
while (iter!=sss.end())
{
QCPItemEllipse *circle = new QCPItemEllipse(ui->widget);
circle->topLeft->setType(QCPItemPosition::PositionType::ptPlotCoords);
circle->bottomRight->setType(QCPItemPosition::PositionType::ptPlotCoords);
circle->topLeft->setCoords( (*iter).x-0.1,(*iter).y-0.1);
circle->bottomRight->setCoords((*iter).x+0.1,(*iter).y+0.1);
iter++;
}
//set temp = get_inters('L',x1,y1,x2,y2);
//sss.insert(temp.begin(), temp.end());
}
if (s[0] == 'R'){
double x1 ,y1, x2, y2;
i = 2;
string num = "";
while(s[i] != ' '){
num = num + s[i];
i++;
}
i++;
x1 = atoi(num.c_str());
num = "";
while(s[i] != ' '){
num = num + s[i];
i++;
}
i++;
y1 = atoi(num.c_str());
num = "";
while(s[i] != ' '){
num = num + s[i];
i++;
}
i++;
x2 = atoi(num.c_str());
num = "";
while(s[i] != '\0'){
num = num + s[i];
i++;
}
y2 = atoi(num.c_str());
QCPItemLine *ray = new QCPItemLine(ui->widget);
ray->setHead(QCPLineEnding::esFlatArrow);
ray->setTail(QCPLineEnding::esBar);
ray->start->setType(QCPItemPosition::PositionType::ptPlotCoords);
ray->end->setType(QCPItemPosition::PositionType::ptPlotCoords);
ray->start->setCoords(x1,y1);
ray->end->setCoords(x2,y2);
sss = get_inters('R',x1,y1,x2,y2);
set::iterator iter = sss.begin();
while (iter!=sss.end())
{
QCPItemEllipse *circle = new QCPItemEllipse(ui->widget);
circle->topLeft->setType(QCPItemPosition::PositionType::ptPlotCoords);
circle->bottomRight->setType(QCPItemPosition::PositionType::ptPlotCoords);
circle->topLeft->setCoords( (*iter).x-0.1,(*iter).y-0.1);
circle->bottomRight->setCoords((*iter).x+0.1,(*iter).y+0.1);
iter++;
}
//set temp = get_inters('R',x1,y1,x2,y2);
//sss.insert(temp.begin(), temp.end());
}
if (s[0] == 'S'){
double x1 ,y1, x2, y2;
i = 2;
string num = "";
while(s[i] != ' '){
num = num + s[i];
i++;
}
i++;
x1 = atoi(num.c_str());
num = "";
while(s[i] != ' '){
num = num + s[i];
i++;
}
i++;
y1 = atoi(num.c_str());
num = "";
while(s[i] != ' '){
num = num + s[i];
i++;
}
i++;
x2 = atoi(num.c_str());
num = "";
while(s[i] != '\0'){
num = num + s[i];
i++;
}
y2 = atoi(num.c_str());
QCPItemLine *seg = new QCPItemLine(ui->widget);
seg->setHead(QCPLineEnding::esHalfBar);
seg->setTail(QCPLineEnding::esHalfBar);
seg->start->setType(QCPItemPosition::PositionType::ptPlotCoords);
seg->end->setType(QCPItemPosition::PositionType::ptPlotCoords);
seg->start->setCoords(x1,y1);
seg->end->setCoords(x2,y2);
sss = get_inters('S',x1,y1,x2,y2);
set::iterator iter = sss.begin();
while (iter!=sss.end())
{
QCPItemEllipse *circle = new QCPItemEllipse(ui->widget);
circle->topLeft->setType(QCPItemPosition::PositionType::ptPlotCoords);
circle->bottomRight->setType(QCPItemPosition::PositionType::ptPlotCoords);
circle->topLeft->setCoords( (*iter).x-0.1,(*iter).y-0.1);
circle->bottomRight->setCoords((*iter).x+0.1,(*iter).y+0.1);
iter++;
}
//set temp =get_inters('S',x1,y1,x2,y2);
// sss.insert(temp.begin(), temp.end());
}
ui->widget->replot();
}
十一,界面模块与计算模块的对接。详细地描述 UI 模块的设计与两个模块的对接,并在博客中截图实现的功能
首先使用VS生成.dll, .lib和.h文件,之后将三个文件拷贝到项目目录中,并将头文件进行修改以保证在执行时能调用dll文件。
修改前头文件:
#pragma once
#include
__declspec(dllexport) class Point //坐标(x, y)
{
public:
Point(double a, double b);
double get_x() const;
double get_y() const;
bool operator<(const Point& p) const;
private:
double x;
double y;
};
__declspec(dllexport) std::set get_inters(char type, double x1, double y1, double x2, double y2);
__declspec(dllexport) std::set get_inters(double p, double q, double r);
修改后:
#pragma once
#pragma comment(lib, "Intersection.lib")
#include
__declspec(dllimport) class Point
{
public:
Point(double a, double b);
double get_x() const;
double get_y() const;
bool operator<(const Point& p) const;
double x;
double y;
};
__declspec(dllimport) std::set get_inters(char type, double x1, double y1, double x2, double y2);
__declspec(dllimport) std::set get_inters(double p, double q, double r);
本次接口主要提供两个求解交点的方法,UI端甚至不需要接口内部的Line和Circle类就可以使用该接口,通过将接口的几何描述输入接口,就可以得到当前几何对象与所有容器内的图形的交点集。
- 文件拖拽输入
//当用户拖动文件到窗口部件上时候,就会触发dragEnterEvent事件
void MainWindow::dragEnterEvent(QDragEnterEvent *event)
{
//如果为文件,则支持拖放
if (event->mimeData()->hasFormat("text/uri-list"))
event->acceptProposedAction();
}
//当用户放下这个文件后,就会触发dropEvent事件
void MainWindow::dropEvent(QDropEvent *event)
{
QList urls = event->mimeData()->urls();
if(urls.isEmpty())
return;
//多个文件取第一个来进行后面的操作
QString fileName = urls.first().toLocalFile();
if (fileName.isEmpty()) {
return;
}
if (readFile(fileName)) {
ui->widget->replot();
}
}
将input.txt拖拽至窗口内即可自动输入并显示交点:
这里我们要求文件最后一行为end表示输入结束
- 增加对象:
- EXit推出程序
十二,描述结对的过程,提供两人在讨论的结对图像资料(比如 Live Share 的截图)。关于如何远程进行结对参见作业最后的注意事项。
我们本次结对编程主要采用腾讯会议进行屏幕共享,并通过QQ聊天交流信息完成。
腾讯会议只能支持单人对于屏幕的操作,但好处是比较稳定,相互交流起来没什么卡顿。
十三,看教科书和其它参考书,网站中关于结对编程的章节,说明结对编程的优点和缺点。同时描述结对的每一个人的优点和缺点在哪里(要列出至少三个优点和一个缺点)。
结对编程的优点
- 结对编程能增加成员的工作积极性。因为在面对问题的时候,会有人一起分担,共同尝试新的策略。
- 两个人一起工作需要互相配合,如果想偷懒去干别的,就会拖延工作进度,故可以起到相互监督的作用
- 在编程中,相互讨论,可以更快更有效地解决问题,互相请教对方,可以得到能力上的互补。
- 两人互相监督工作,可以增强代码和产品质量,并有效的减少BUG。
结对编程的缺点
- 与合不来的人一起编程容易发生争执,扰乱项目正常进行
- 开发人员可能会在工作时交谈一些与工作无关的事,分散注意力,造成效率低下
队友的优点
- 性格随和,善于沟通,有利于项目上的交流
- 态度积极,一起合作完成项目
- 执行力强,写代码速度快
队友的缺点
- 有时会出现粗心Bug,大家一起改正
我的优点
- 思考严谨,在写代码之前会先考虑可行性
- 学习能力强,对于新知识有一定的自学能力
- 结对编程态度也比较积极,不耽误小组进度
我的缺点
- 代码能力稍弱,写代码耗时较长