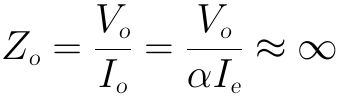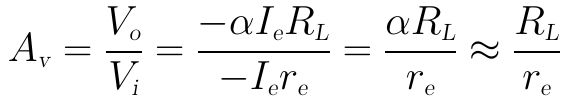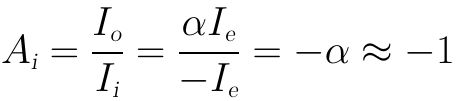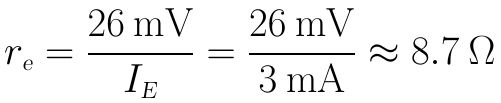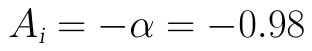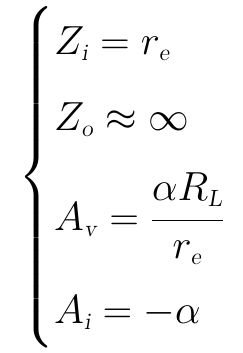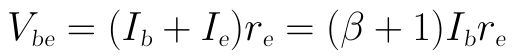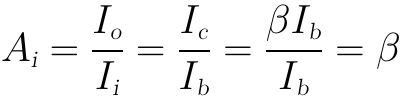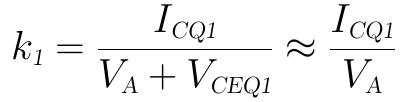回到目录
re建模的基本思路是,将BJT晶体管的输入端口(通常为发射结)近似视为一个等效二极管,将输出端端口(通常为集电极和一个公共端子,公共端子是B还是E,取决于电路是共基接法还是共射接法)近似视为一个等效的受控电流源。
下面我们分别详细介绍共基、共射、共集组态的re模型。
1. 共基组态
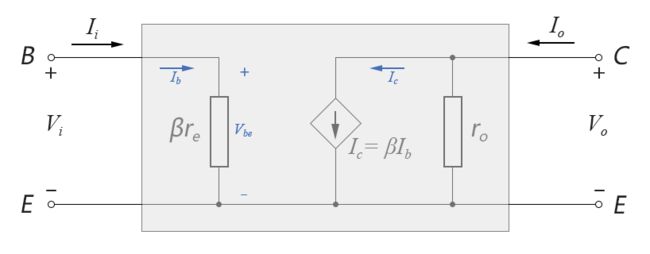
共基组态的基本接法和近似等效电路如下图所示,我们这里先对npn型晶体管进行分析:
图4-4.01
图中,黑色字体的v和i是标准二端口的规定方向,而实际BJT中的电压电流方向我们用蓝色予以表示。
注意上面电路中的电压/电流符号用的都是交直流总和形式,下面我们进行直流和交流的分离:对于二极管,在静态工作点附近可等效视为为一个交流电阻(参见:1-4 二极管的电阻);而对于受控电流源,其直流α参数和交流α参数是非常接近的。因此,可以得到纯交流部分的等效电路如下图所示:
图4-4.02
对于纯交流电路,我们所有的电压电流参数使用的都是相量表示法(变量大写、下标小写,如:Vi、Ie),这个和交流分量的写法(如:vi、ie)的含义是一致的,写成相量形式表示法,对今后的计算会比较方便。
(题外话:在电路基本理论中,这个名词的写法是“相量”(phasor),不是数学中的“向量”(vector),相量是一个复数!)
下面我们计算共基组态re模型的4个典型交流参数:(交流)输入阻抗、(交流)输出阻抗、(交流)电压放大倍数、(交流)电流放大倍数。为叙述简洁,人们一般都会省略“交流”两字,但你心里要清楚,这4个量都是基于交直流分离后的纯交流电路而言的。
● 输入阻抗:
输入阻抗比较简单,从图中一眼就可以看出,输入阻抗就是二极管交流电阻:
● 输出阻抗:
从上图4-4.02中可以看到,在二端口的输出部分是一个受控电流源,其电流仅受输入端的电流Ie控制,基本不受输出端电压Vo的影响。根据电路理论,理想电流源的内阻为无穷大(不管是独立电流源还是受控电流源),因此,输出阻抗为无穷大。
比如:假设将输入电流Ie置于0,则输出电流Ic也为0,不管在输出端外加多大的电压Vo,输出端口始终无电流通过,相当于开路状态。则根据输出电阻的定义式:
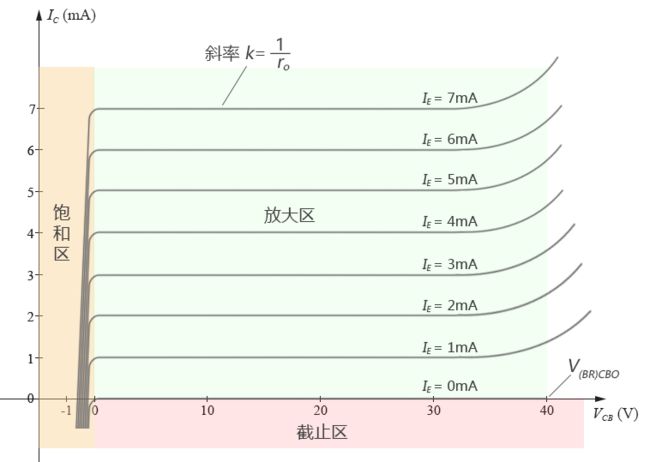
事实上,上面这个结论只是由我们的re简化模型的电路图得出的理想情况。共基组态真实的输出阻抗应该从晶体管共基组态的输出曲线上读出。从下图的共基组态输出曲线中可以看出,在放大区,每一根“输出总电压(VCB)”与“输出总电流(Ic)”曲线的斜率都接近水平(即斜率k接近于0),则动态电阻(为斜率k的倒数)接近无穷大,但并不是真正的无穷大。一般根据厂商的实测数据,共基组态的BJT晶体管的输出阻抗Zo通常都在兆欧级。在通常的简化计算中,我们将其近似看作无穷大。
图4-4.03
● 电压放大倍数:
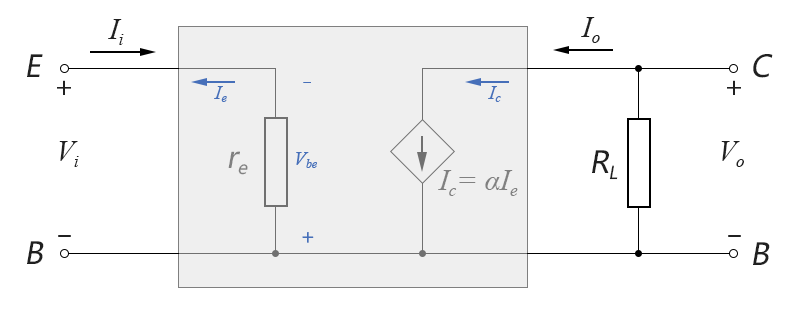
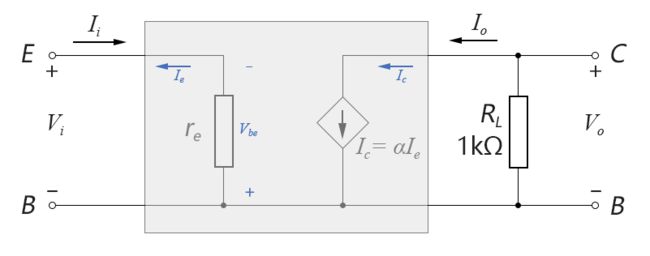
计算电压放大倍数,需要在输出端接上负载电阻,如下图所示:
图4-4.04
输入电压Vi和输出电压Vo分别为:
因此电压放大倍数为:
说明:从上式可以看到,共基放大电路的电压放大倍数不仅取决于BJT本身的性能,还取决于外接的负载电阻RL的值。
● 电流放大倍数:
电流放大倍数为输出电流Io和输入电流Ii的比值:
案例4-4-1:对于下图的共基组态re等效模型,已知IE=3mA,α=0.98,试求:(1)输入阻抗;(2)电压放大倍数;(3)电流放大倍数;
图4-04.a1
解:(1)输入阻抗re由二极管的静态工作电流决定:
(2)电压放大倍数为:
(3)电流放大倍数为:
对于pnp型晶体管,其分析方法也是类似的,只是其中有些电流与电压的方向不同:输入电流iI与输入端口的实际电流iE同方向;输出电流iO与输出端口的实际电流iC反向,如下图所示:
图4-4.05
其4个典型交流参数的最终计算结果与npn型的结论是一致的:
2. 共射组态
共射组态的基本接法和近似等效电路如下图所示,我们这里同样先对npn型晶体管进行分析:
图4-4.06
然后进行直流和交流的分离:对于二极管,在静态工作点附近可等效视为为一个交流电阻;而对于受控电流源,其直流β参数和交流β参数也是非常接近的。因此,可以得到纯交流部分的等效电路如下图所示:
图4-4.07
下面我们计算共基组态re模型的4个典型交流参数:
● 输入阻抗:
输入阻抗的计算式为:
而Vbe为:
将Vbe代入上式得:
对于共射组态,一般的β典型值在几十到几百左右,re的典型值大概为几欧到十几欧左右,故输入阻抗Zi的典型值一般为几kΩ量级。
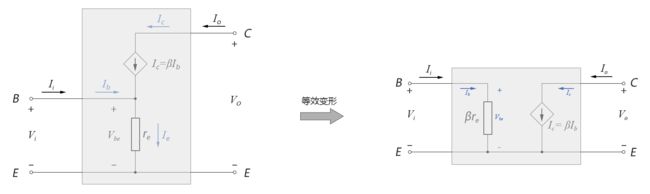
算出输入阻抗后,我们可以对共射组态的re模型电路作等效变形,把输入和输出的电路分离开,如下图所示的样子:
图4-4.08
输入阻抗化为一个独立的βre(严格来讲应该是(1+β)re,近似为βre),输出电流仍然同Ic,并且受Ib控制。电路作了以上等效变形后,在后续的计算上会方便很多。后文中,我们都将使用这个等效变形后的共射组态re模型电路。
● 输出阻抗:
在二端口的输出部分是一个受控电流源,其电流仅受输入端的电流Ib控制,基本不受输出端电压Vo的影响。根据电路理论,理想电流源的内阻为无穷大(不管是独立电流源还是受控电流源),因此,输出阻抗为无穷大。
比如,假设将输入电流Ib置于非常小(近似于0),则根据输出电阻的定义式:
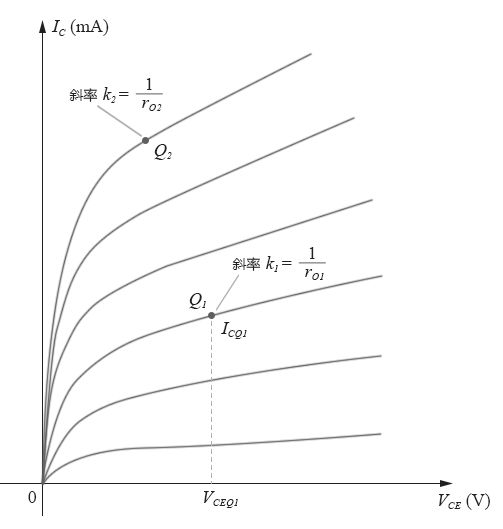
同样的,上面这个式子只是由re简化模型的电路图得出的理想情况。真正的输出阻抗应该从晶体管共射组态的输出曲线上读出,其输出曲线如下图所示。
图4-4.09
输出阻抗实质上就是输出曲线的动态电阻。不过和共基组态相比,共射组态的各条输出曲线并不那么水平,因此,其真正的输出阻抗要比共基组态小得多,其在各点的输出阻抗即为输出曲线在这个点处的斜率的倒数,而且在不同点的输出阻抗都不相同。静态集电极电流IC越大,则斜率越陡,输出阻抗越小。
一般厂商在数据手册中都会给出几个典型工作点的测试数据,对于共射组态的输出阻抗Zo,其典型值大约在几十kΩ左右。
下图是修正过的共射组态的re模型,图中加上了非理想输出电阻ro的影响:
图4-4.10
● 电压放大倍数:
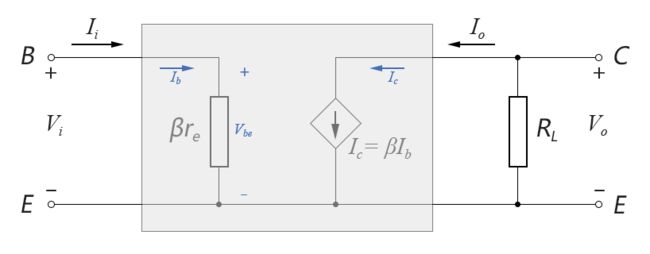
计算电压放大倍数,需要在输出端接上负载电阻,为简化说明概念,我们暂时先不考虑非理想输出电阻ro的影响。如下图所示:
图4-4.11
输入电压Vi和输出电压Vo分别为:
因此电压放大倍数为:
说明:从上式可以看到,共射放大电路的电压放大倍数也不仅取决于BJT本身的性能,还取决于外接的负载电阻RL的值。负号表明,输出电压和输入电压的方向相反。
● 电流放大倍数:
电流放大倍数为输出电流Io和输入电流Ii的比值:
● 厄利电压:
我们回顾一下上面的共射组态的输出特性曲线(图4-4.09),虽然各条曲线的斜率都各不相同,但它们之间其实是有规律的,所有的放大区的直线反向延长后都会交于一点,如下图所示:
图4-4.12
这个规律最早在1952年由James M. Early发现的,故图中这个交点处的电压VA称为Early电压(厄利电压)。一般厄利电压的典型值在50~300V左右。知道了这个特性,输出阻抗(即输出曲线的动态电阻)就可以从静态电压电流计算得到,上图中Q1点处的斜率为:
由于VCEQ一般比VA小一个数量级,故上式可近似为:
故在静态工作点Q1处的输出阻抗为:
关于厄利电压,一般只要知道一下其原理即可,实际应用中不常会用到。
3. 共集组态
对于共集电极组态,通常采用和共射组态相同的re模型,其主要的应用就是“射极跟随器”,在后面的章节中我们会详细分析。
回到目录
( end of 4-4)