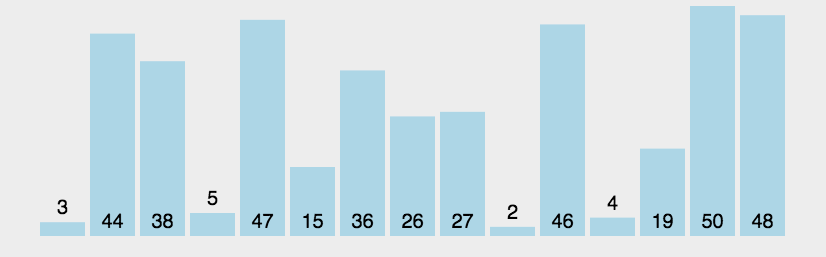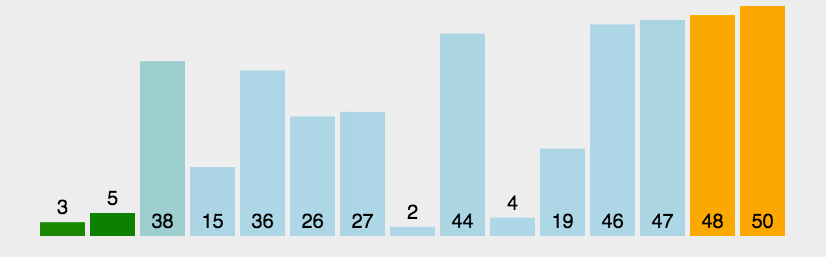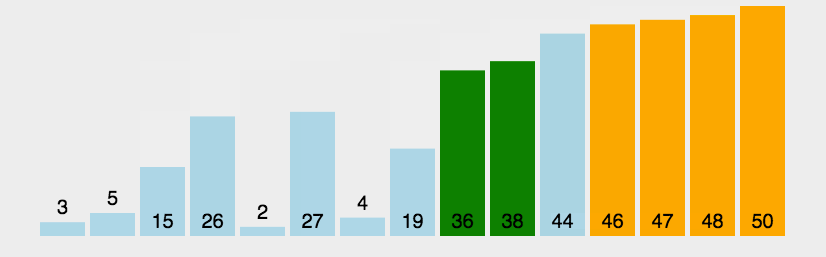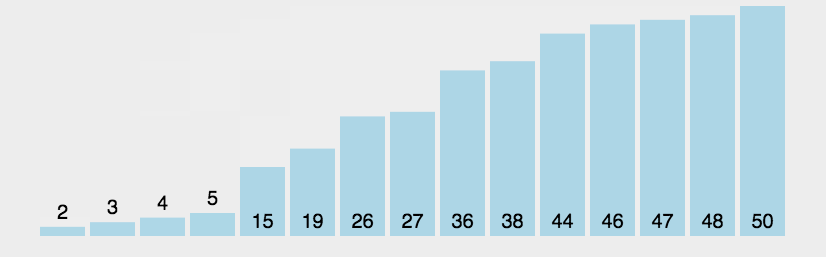常用排序算法总结

排序算法

1. 排序算法概述

1.1 什么是排序算法？

对一序列对象根据某个关键字，按照某种规则进行排序

1.2 排序术语

• 稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面
• 不稳定：如果a原本在b的前面，而a=b，排序之后a可能会出现在b的后面
• 内排序：所有排序操作都在内存中完成
• 外排序：由于数据太大，因此把数据放在磁盘中，而排序通过磁盘和内存的数据传输才能进行
• 时间复杂度： 一个算法执行所耗费的时间。
  空间复杂度：运行完一个程序所需内存的大小

1.3 算法总结

• （注意：n指数据规模；k指“桶”的个数；In-place指占用常数内存，不占用额外内存；Out-place指占用额外内存）

1.4 算法分类

1.5 比较排序与非比较排序

1.5.1 比较排序

• 常见的快速排序、归并排序、堆排序、冒泡排序等属于比较排序。在排序的最终结果里，元素之间的次序依赖于它们之间的比较。每个数都必须和其他数进行比较，才能确定自己的位置。在冒泡排序之类的排序中，问题规模为n，又因为需要比较n次，所以平均时间复杂度为\(O(n²)\)。在归并排序、快速排序之类的排序中，问题规模通过分治法消减为\(log n\)次，所以时间复杂度平均\(O(nlogn)\)。比较排序的优势是，适用于各种规模的数据，也不在乎数据的分布，都能进行排序。可以说，比较排序适用于一切需要排序的情况。

1.5.2 非比较排序

• 计数排序、基数排序、桶排序则属于非比较排序。非比较排序是通过确定每个元素之前，应该有多少个元素来排序。针对数组arr，计算arr[i]之前有多少个元素，则唯一确定了arr[i]在排序后数组中的位置。非比较排序只要确定每个元素之前的已有的元素个数即可，所有一次遍历即可解决。算法时间复杂度\(O(n)\)。非比较排序时间复杂度底，但由于非比较排序需要占用空间来确定唯一位置。所以对数据规模和数据分布有一定的要求。

---

2. 排序算法具体实现

2.1 冒泡排序

2.1.1 算法思想

• 冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

2.1.2 算法描述

1. 比较相邻的元素。如果第一个比第二个大，就交换它们两个

2. 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样在最后的元素应该会是最大的数；

3. 针对所有的元素重复以上的步骤，除了最后一个；

4. 重复步骤1~3，直到排序完成。

   从前往后将最大的拍到后面

   

   从后往前将最小的排到前面

   

2.1.3 算法实现

（1）数组线性表

/**
 * 冒泡排序-数组线性表排序算法
 */
public void bubbleSort(){
    if(this.size <= 1){
        return ;
    }
    for(int i = 0;i)objects[j+1]).compareTo((E)objects[j])<0){
                Comparable temp =(Comparable) objects[j+1];
                objects[j+1] = objects[j];
                objects[j] = temp;
                didSwap = true;
            }
        }
        if(!didSwap){
            return ;
        }
    }
}

（2）链式线性表

/**
 * 冒泡排序-链式表排序算法
 */
public void bubbleSort(){
    if(this.head.next == null||this.head.next.next==null){
        return ;
    }
    //后面已经浮上来的（排好序的）头结点
    Node sortedHead = null;
    //第一个存储元素的结点
    Node first = head.next;
    for(Node outCur = head.next;outCur!=null;outCur = outCur.next){
        Node cur = first;
        for(Node afterCur = first.next;afterCur!=sortedHead;afterCur = afterCur.next,cur = cur.next){
            if(cur.elem.compareTo(afterCur.elem)>0){
                Node.swapElem(cur, afterCur);
            }
        }
        sortedHead = cur;
    }
}

2.1.4 算法分析

• 最佳情况：\(T(n) = O(n)\)
  • 此时数组为正序排列，如果第一次检测没有发生交换，则可以认为为正序排列，则可以直接退出
• 最差情况：\(T(n) = O(n^2)\)
  • 逆序排列，对于每个位置都需要进行交换
• 平均情况：\(T(n) = O(n^2)\)

---

2.2排序

2.2.1 算法思想

• 选择排序(Selection-sort)是一种简单直观的排序算法。它的工作原理：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

2.2.2 算法描述

n个记录的直接选择排序可经过n-1趟直接选择排序得到有序结果。具体算法描述如下：

1. 初始状态：无序区为\(R[1..n]\)，有序区为空；

2. 第i趟排序\((i=1,2,3…n-1)\)开始时，当前有序区和无序区分别为\(R[1..i-1]\)和\(R(i..n）\)。该趟排序从当前无序区中-选出关键字最小的记录 \(R[k]\)，将它与无序区的第1个记录R交换，使\(R[1..i]\)和\(R[i+1..n)\)分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区；

3. n-1趟结束，数组有序化了。

2.2.3 算法实现

（1）数组线性表

public class SelectionSorter> implements Sorter {
    @Override
    public void sort(E[] elemArr){
        for(int i = 0;i < elemArr.length;i++){
            int minIndex = i;
            for(int j = i;j

（2）链式线性表

/**
 * 插入排序
 */
public void selectionSort(){
    if(this.head.next==null||this.head.next.next==null){
        return ;
    }

    for(Node outCur = head.next;outCur!=null;outCur = outCur.next){

        Node innerCur = outCur;
        Node afterInnerCur = innerCur.next;
        Node minNode = outCur;
        for(innerCur = outCur;afterInnerCur!=null;innerCur = innerCur.next,afterInnerCur = afterInnerCur.next){
            if(innerCur.elem.compareTo(minNode.elem)<0){
                minNode = innerCur;
            }
        }
        Node.swapElem(outCur,minNode);
    }
}

---

2.3 插入排序

2.3.1 算法思想

• 插入排序（Insertion-Sort）的算法描述是一种简单直观的排序算法。
• 它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。
• 插入排序在实现上，通常采用in-place排序（即只需用到O(1)的额外空间的排序），因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。

2.3.2 算法描述

1. 从第一个元素开始，该元素可以认为已经被排序

2. 取出下一个元素，在已经排序的元素序列中从后向前扫描

3. 如果该元素（已排序）大于新元素，将该元素移到下一位置

4. 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置

5. 将新元素插入到该位置后

6. 重复步骤2~5

   

   

2.3.3 算法实现

public class InsertSorter> implements Sorter {
    @Override
    public void sort(E[] arr) {
        for (int i = 1; i < arr.length; i++) {
            for (int j = i;j > 0;--j) {
                if (arr[j].compareTo(arr[j - 1]) < 0) {
                    E temp = arr[j];
                    arr[j] = arr[j - 1];
                    arr[j - 1] = temp;
                } else {
                    break;
                }
            }
        }
    }
}

2.3.4 算法分析

• 最佳情况：\(T(n) = O(n)\) 序列本身有序（每次选取的第一个无序点都大于有序序列的最大值）
• 最差情况：\(T(n) = O(n^2)\) 序列为逆序（每次选取的无序序列都需要移动到有序序列最前面\(1+2+...+(n-1)=\frac{(n-1)n}{2}\)）
• 平均情况：\(T(n) = O(n^2)\)

---

2.4 希尔排序

2.4.1 算法思想

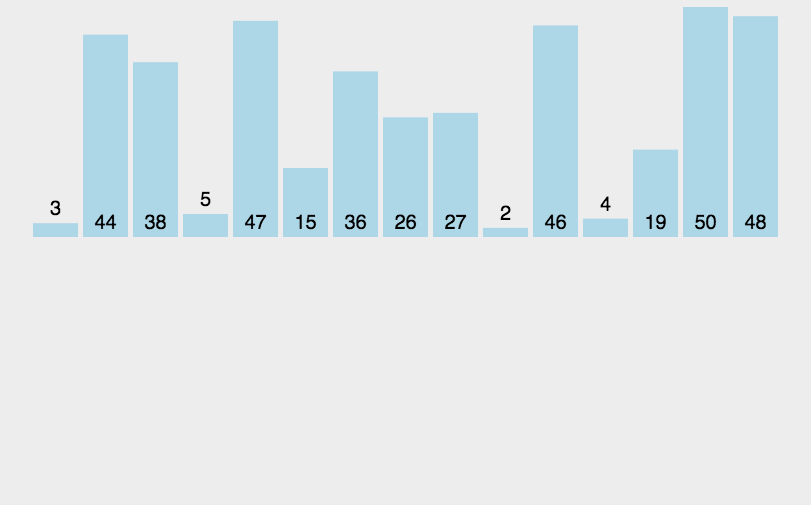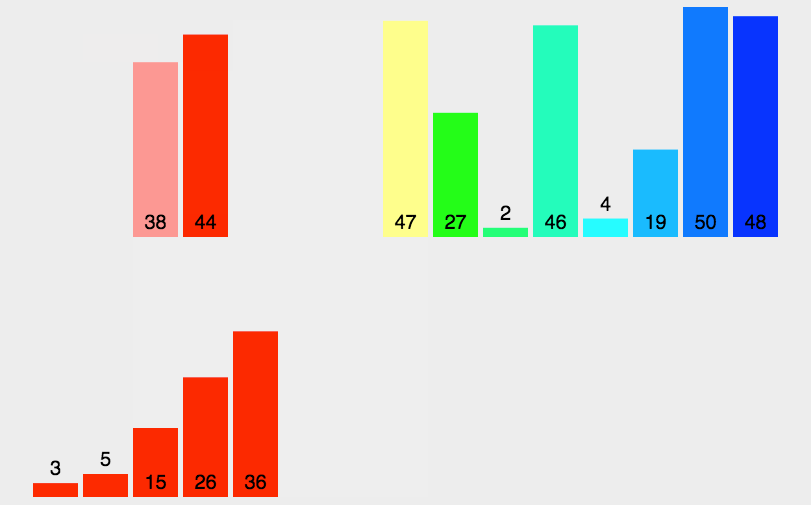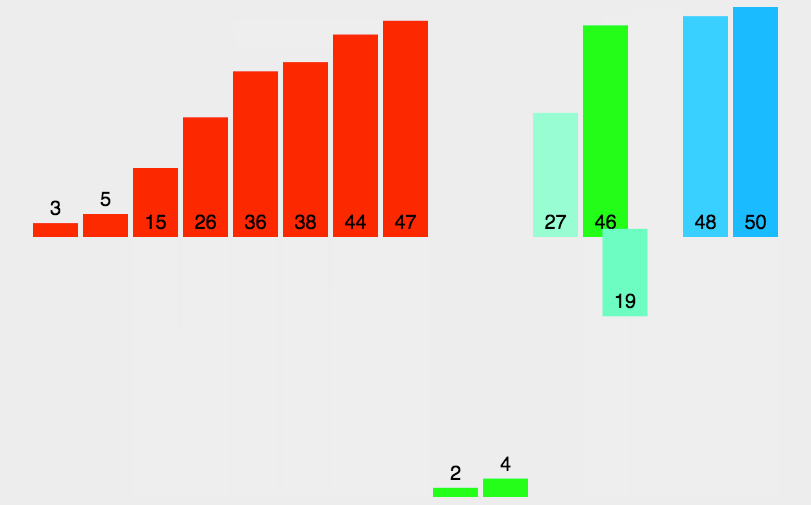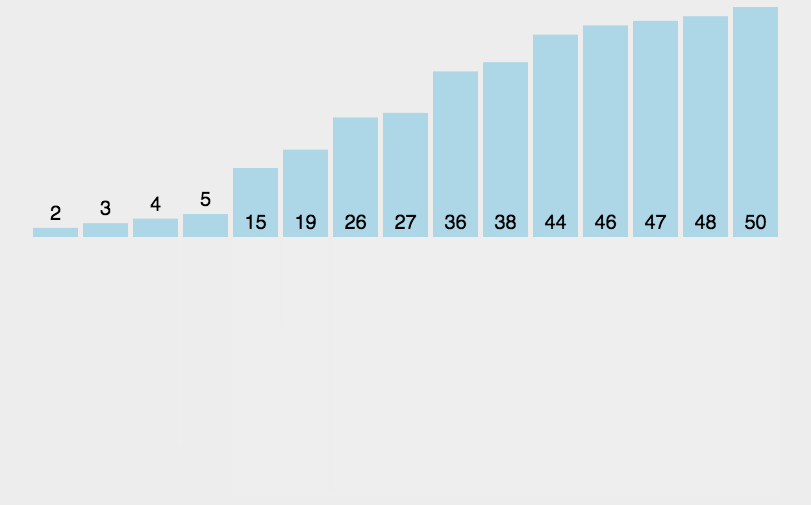
• 希尔排序也是一种插入排序，它是简单插入排序经过改进之后的一个更高效的版本，也称为缩小增量排序，同时该算法是冲破\(O(n^2)\)的第一批算法之一。
• 它与插入排序的不同之处在于，它会优先比较距离较远的元素。
• 希尔排序又叫缩小增量排序。希尔排序是把记录按下表的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止
• 该方法实质上是一种分组插入方法
• 增量序列的最后一个增量值必须等于1

2.4.2 算法描述

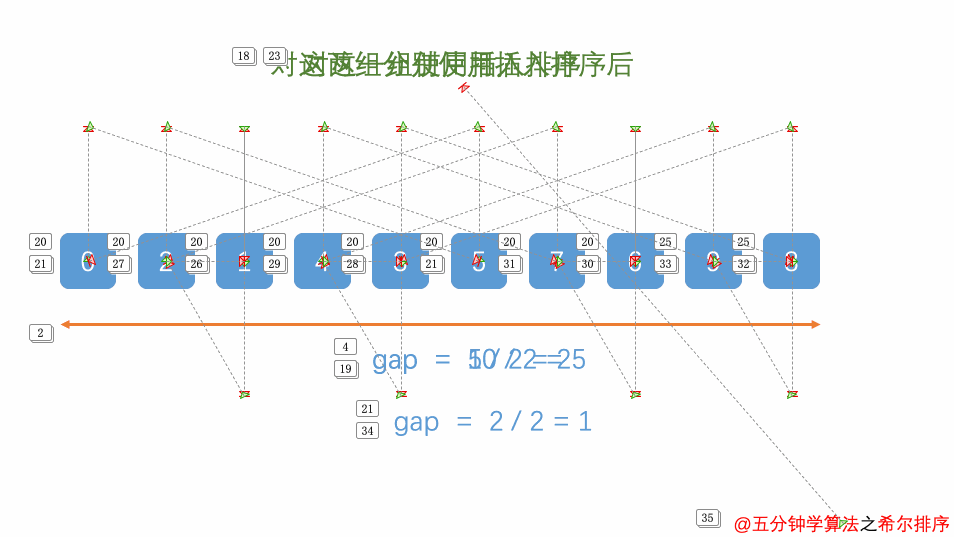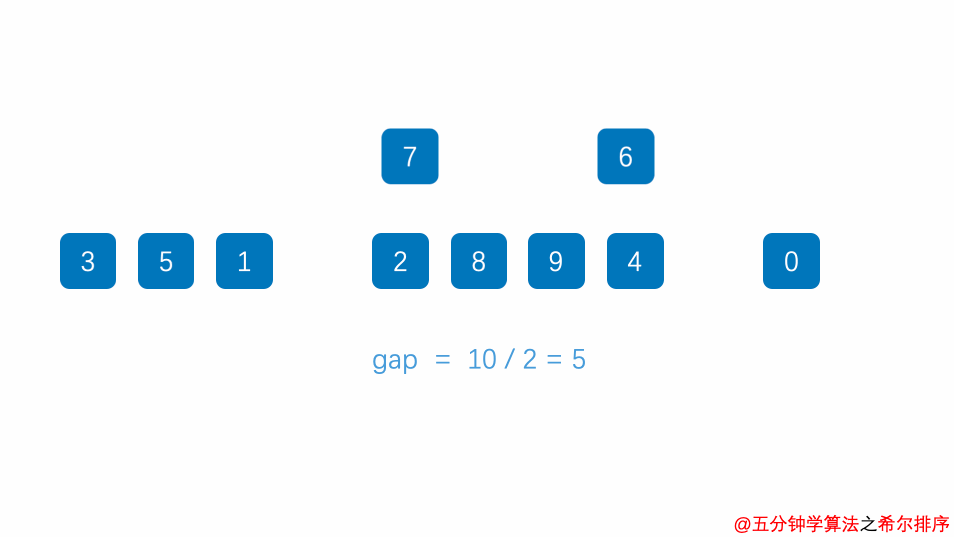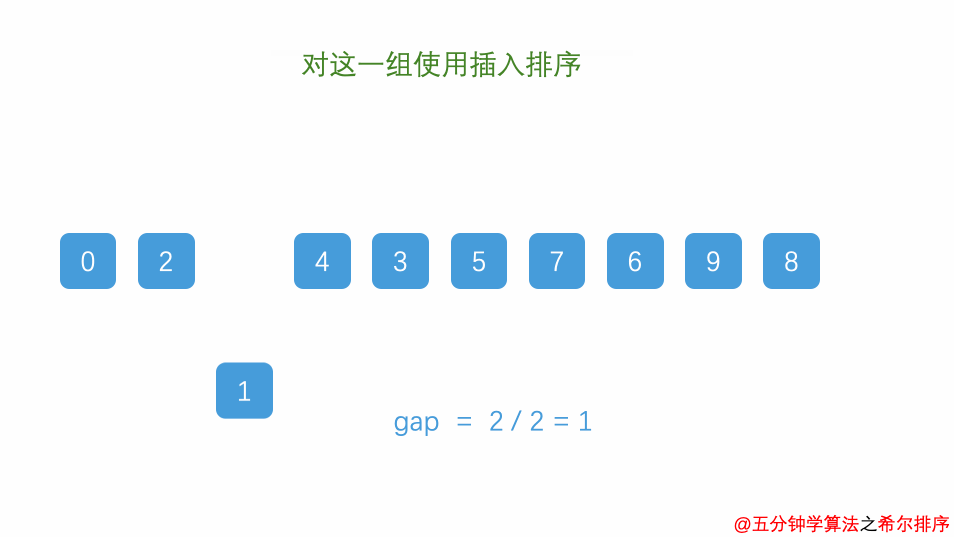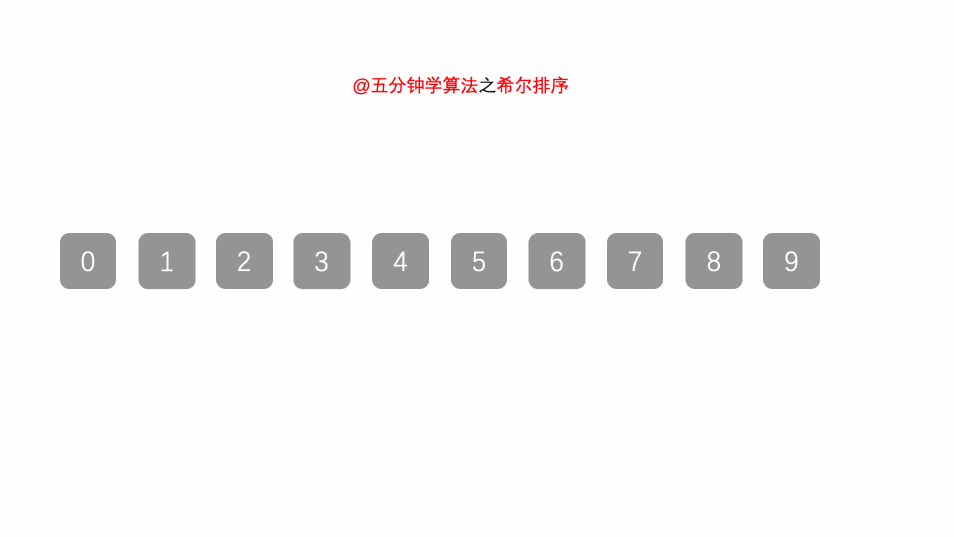
1. 选择增量\(gap=length/2\)，缩小增量继续以\(gap = gap/2\)的方式，这种增量选择我们可以用一个序列来表示，\(T=\{n/2,(n/2)/2,...,1\}\)，称为增量序列。
   • 采用上述增量序列因为增量序列难以通过数学证明求出，所以选择一个常用的增量序列 ，上述增量序列也被称为希尔增量。
     • 但其实这个增量序列不是最优的
2. 按增量序列个数k，对序列进行k 趟排序
3. 每趟排序，根据对应的增量ti，将待排序列分成若干长度为m 的子序列，分别对各子表进行直接插入排序。
4. 仅增量因子为1时，整个序列作为一个表来处理，表长度即为整个序列的长度
   
5. 

2.4.3 算法实现

package com.sort;


/**
 * @author Ni187
 */
public class ShellSorter> implements Sorter {
    @Override
    public void sort(E[] arr) {
        for (int gap = arr.length / 2; gap > 0; gap /= 2){
            for(int i=gap; i=0&&arr[j].compareTo(arr[j+gap])>0; j=j-gap){
                    E temp = arr[j];
                    arr[j] = arr[j+gap];
                    arr[j+gap] = temp;
                }
            }
        }
    }
}

2.4.4 算法分析

• 最佳情况：\(T(n)=O(n^2)\)
• 最坏情况：\(T(n)=O(nlog(2n))\)
• 平均情况：\(T(n)=O(nlog(2n))\)

---

2.5 归并排序

2.5.1 算法思想

• 归并排序是建立在归并操作上的一种有效的排序算法。
• 该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。
• 归并排序是一种稳定的排序方法。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并

2.5.2 算法描述

1. 把长度为n的输入序列分成两个长度为n/2的子序列

2. 对这两个子序列分别采用归并排序

3. 将两个排序好的子序列合并成一个最终的排序序列
   

   

2.5.3 算法实现

package com.sort;

import java.util.Arrays;

/**
 * @author Ni187
 */
public class MergeSorter> implements Sorter {

    @Override
    public void sort(E[] arr) {
        Object[] mergedArr = new Object[arr.length];
        sort(arr, 0, arr.length-1,mergedArr);
    }

    public void sort(E[] arr, int left, int right,Object[] mergedArr) {
        if (right<=left) {
            return;
        }
        int mid = (left + right) / 2;
        sort(arr, left, mid,mergedArr);
        sort(arr, mid+1 , right,mergedArr);
        merge(arr, left, mid, right,mergedArr);
    }

    private void merge(E[] arr, int left, int mid, int right,Object[] mergedArr) {
        int i = left;
        int j = mid + 1;
        int index = 0;
        while (i <= mid && j <= right) {
            if (arr[i].compareTo(arr[j]) <= 0) {
                mergedArr[index++] = arr[i++];
            } else {
                mergedArr[index++] = arr[j++];
            }
        }
        while (i <= mid) {
            mergedArr[index++] = arr[i++];
        }
        while (j <= right) {
            mergedArr[index++] = arr[j++];
        }
        index = 0;
        while(left <= right){
            arr[left++] = (E)mergedArr[index++];
        }
    }

}

2.5.5 算法分析

• 每次合并操作的平均时间复杂度为\(O(n)\)，而完全二叉树的深度为\(logn\)。总的平均时间复杂度为\(O(nlogn)\)
• 归并排序的最好，最坏，平均时间复杂度均为\(O(nlogn)\)
• 由于使用辅助数组来存储归并的数组，空间复杂度为\(O(n)\)

---

2.6 快速排序

2.6.1 算法思想

• 通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序

2.6.2 算法描述

1. 从数列中挑出一个元素，称为 “基准”（pivot）；
2. 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作
   • 挖坑法
   • 交换法
3. 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序
   

2.6.3 算法实现

• 此处使用交换法实现

package com.sort;

import java.util.Random;

/**
 * @author Ni187
 */
public class QuickSorter> implements Sorter {
    @Override
    public void sort(E[] arr) {
        QuickSort(arr, 0, arr.length-1);
    }

    public  void QuickSort(E[] array, int start, int end) {
        if (start > end) {
            return ;
        }
        int smallIndex = partition(array, start, end);
        QuickSort(array, start, smallIndex - 1);
        QuickSort(array, smallIndex + 1, end);
    }

    public int partition(E[] array, int left, int right) {
        int pivot = (int) (left + Math.random() * (right - left));
        E basic = array[pivot];
        while(left!=right){
            while(left < right && array[right].compareTo(basic)>=0){
                right--;
            }
            while(left < right && array[left].compareTo(basic)<=0){
                left++;
            }
            swap(array, left, right);
        }
        array[left]=basic;
        return left;
    }

    public void swap(E[] array, int i, int j) {
        E temp = array[i];
        array[i] = array[j];
        array[j] = temp;
    }
}

2.5.4 算法分析

• 最好情况：每次选择的基数恰好把两侧分开（左侧小于基数，右侧大于基数），每次扫描n,共分成logn,时间复杂度为\(O(logn)\)
• 最坏情况：每次选择的基数恰好位于两侧之一，每次扫描n,共分成n,时间复杂度为\(O(n^2)\)
• 平均：复杂度\(O(n\log n)\)