数据结构的分类
1.集合结构;
2.线性结构;一对一的关系
3.树型结构;一对多的关系
4.图形结构。多对多的关系
基于数组实现的数据结构
数组为什么需要指定长度?
想象一下,如果不指定长度的话,内存空间一次性得开辟多少连续的空间,我们是不能确定的。
因为数组是内存空间中连续的空间,这样是为了数组的连续编号性。所以到哪里截止就是一个需要确定的问题。
数组最大的优点:快速查询,所以数组最好应用于索引有语义的情况。
缺点:不能动态的开辟空间。每次开辟空间都得进行一轮复制操作。
动态数组
java中的动态数组
在java中,就是指ArrayList,在添加或删除元素时,都需要根据当前容器的大小来动态控制内部数据的大小。
细节点
第一,扩容的大小:与当前数量级成正比最好,所以每次扩容都是当前数组量的2倍。
第二,数字得size其实就是下一个待添加元素的索引。
涉及到复杂度的两个概念
均摊复杂度:一个相对比较耗时的操作,如果不是每次都触发的话,那么可以分摊到其他操作过程中去。
复杂度的震荡:在某些特殊情况下或者操作下,复杂度突然增加。
栈
后进先出:俄罗斯方块,往一个容器里放盒子。
队列
先进先出:生活中的排队。
普通队列:出队操作O(n)复杂度,每次出队时,需要对整个数据进行一次前移操作。由此出现了循环队列,多一个front指针来指向前节点。
注意点:对front和tail的操作需要考虑%(取余)操作,让指针循环起来。
链表
性质:一种真正的动态数据结构。在添加元素等逻辑操作时,为了统一处理逻辑,增加虚拟头节点。
基于链表也可形成栈和队列,形成栈时,由于只在第一个元素进行操作,所以可直接基于链表这种数据结构进行实现。但形成队列的时,会涉及到头部与尾部的操作,所以需要添加一个尾指针,尾部作入队操作,头部作出队操作。
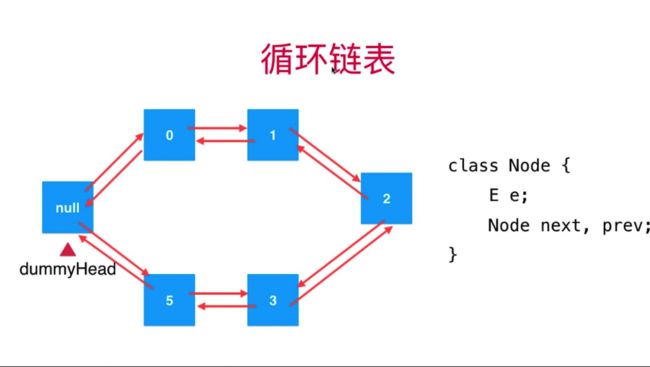
循环双向列表:先看双向链表,每个元素都包含上一个元素和下一个元素节点,再看循环链表,就是增加一个头指针和尾指针;再看形成了闭环的循环链表,可以只维护头指针,因为整体是循环的,可以看成一个圆,然后增加一个虚拟头节点,向头部添加元素就是向虚拟头节点后插入元素,向尾部添加元素就是向虚拟头节点前插入元素。如下图:
链表与数组的对比
链表的优势在于(取自bobo老师问答区总结):
1,节省空间,由于不是静态分配内存,没有空间浪费
2,不需要resize。在不停的添加且删除元素的过程中,如果经常触发resize,resize本身会很耗时。
3,如果你存储的数据没有顺序性要求,换句话说,如果你不会在特定位置插入或者删除元素,而只会在头尾插入或者删除元素的话,链表的时间复杂度是O(1)的!对于数组,只有在数组末尾添加元素,才是O(1)级别,而且是均摊后的结果。
4,对于java.util.LinkedList底层的双链表来说,在指定位置插入元素,或者删除指定位置的元素,实际最多只需要遍历n/2个元素就好了。虽然复杂度依然是O(n)的,但当元素个数没有超过一定限制的时候,平均比动态数组的O(n)快。
另外,对于链表来说,插入操作性能消耗点:
第一,寻址过程;
第二,不断new新的节点过程。
双向循环列表带来的寻址过程的优势,只有在一定数量级内才会体现出来。
递归
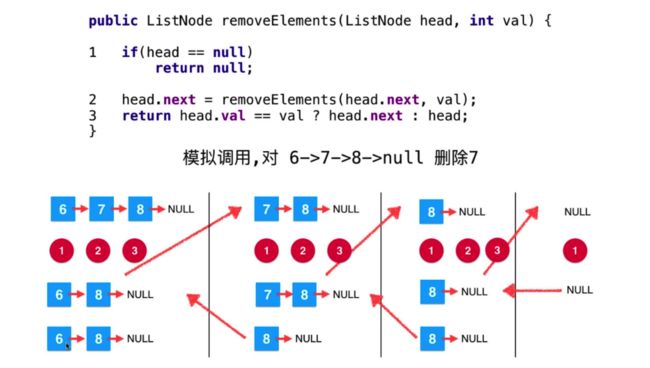
递归算是链表和树这类数据结构中应用最为广泛的一种实现方式。下图展示在链表中删除某一个元素的递归微观过程。
树结构
基本介绍
局限性:元素必须有可比性。
在满二叉树情况下,因为节点个数n与树的高度h存在2的h次方等于n的关系,所以增,删,查都是O(logn)级别,假如以2为底,操作次数之间的差别如下:
| num | log(n) | n | 相差倍数 |
|---|---|---|---|
| 16 | 4 | 16 | 4 |
| 1024 | 10 | 1024 | 100 |
| 100万 | 20 | 100万 | 5万 |
注意点:
对于树结构,删除操作需要找寻后继元素,移除最小元素,这两个操作也是Olog(n)级别。
java中的TreeSet,底层基于红黑树进行实现,保证了添加元素后不会退化成链表而影响性能。
完全二叉树:元素都是从最左边开始码放。
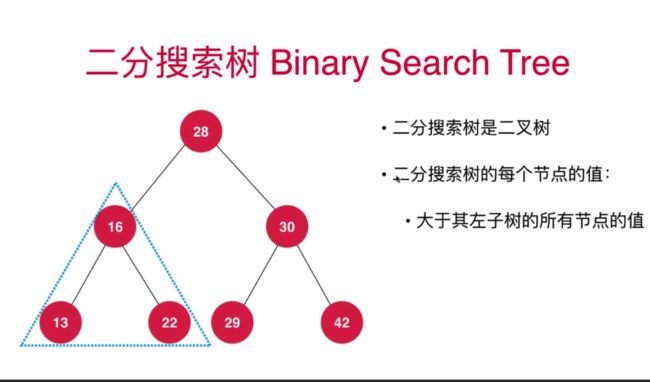
二分搜索树
任意节点左子树的值都小于节点值,右子树的值都大于节点值。
缺点:在极端情况下,有可能退化成链表。
之所以高效,是因为在每次查询的时候都能去除一半的数据。
查询元素:涉及到前序遍历,中序遍历,后续遍历,层序遍历。
删除元素:分三种情况来讨论,删除节点的左子树为空,删除节点的右子树为空,删除节点的左右子树都不为空。
平衡二叉树
定义:最大深度和最小深度相差为1。
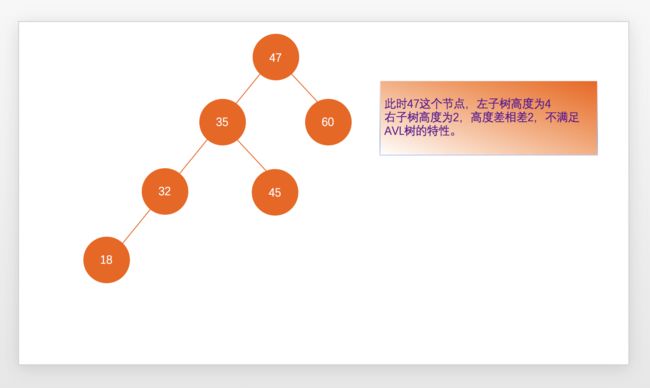
AVL树
二分搜索树在特殊的情况下会退化成链表,为了维持树的自平衡性,科学家们发明了AVL自平衡树。
特点如下:
1.满足二分搜索树所有性质;
2.带有平衡条件:每个结点的左右子树的高度之差的绝对值(平衡因子)最多为1。
trie
trie是一种多叉树,因为多个指针(假设为n)的缘故,一次查看操作就会去除 n-1/n 数据。
缺点:空间消耗
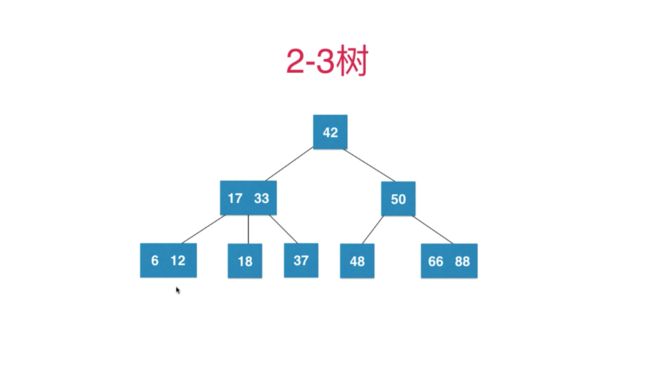
2-3树
1.满足二分搜索树基本性质。
2.二节点存放两个元素。
3.三节点存放两个元素,有三个孩子。
4.三节点,左孩子节点小于父亲节点中的最小值,中孩子节点介于父亲节点左右节点中,有孩子节点大于父亲节点中任意节点。
绝对平衡树:从根节点到任意一个叶子节点所经过的节点数量一定是相同的。2-3树是一颗绝对平衡树
由于水平有限,如有错误,欢迎指出,后续还会不断完善。本文图片转自慕课网玩转数据结构课程,侵删