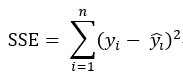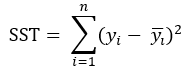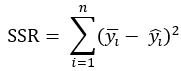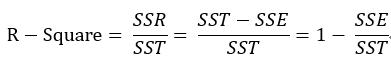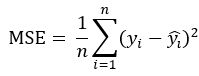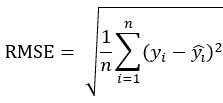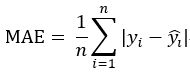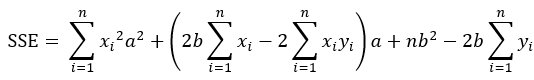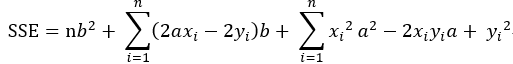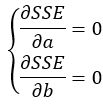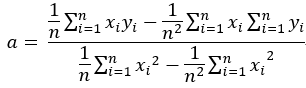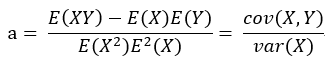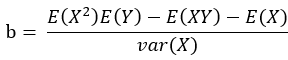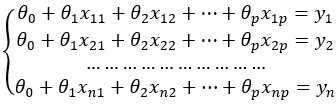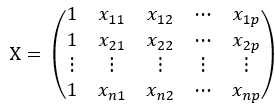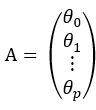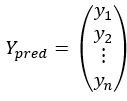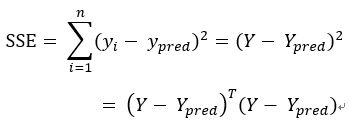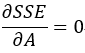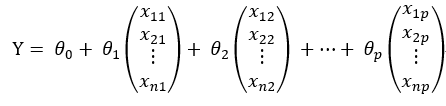最小二乘法的回归方程求解
最近短暂告别大数据,开始进入到了算法学习的领域,这时才真的意识到学海无涯啊,数学领域充满了无限的魅力和乐趣,可以说更甚于计算机带给本人的乐趣,由于最近正好看到线性代数,因此,今天我们就来好好整理一下机器学习领域中的一个非常重要的算法——最小二乘法,那么,废话不多说,我们直接开始吧 !
1. 最小二乘法介绍
1.1 举例
现实生活中,我们经常会观察到这样一类现象,比如说某个男的,情商很高,身高180,家里很有钱,有房,有车,是个现充,结果就是他有好几个女朋友,那么从一个观测者的角度来看,该男性具备好多个特征(比如EQ值较高,身高较高,有钱对应的布尔值是True等等),输出结果就是女友的个数;这只是一条记录,那么,当我们将观测的样本数扩大到很多个时,每个个体作为输入,而输出就是每个个体的女朋友数量;于是在冥冥之中,我们就能感觉到一个男性拥有的女友数量应该和上述特征之间存在着某种必然的联系。然后可以这样理解,决定一个男性可以交到女友数量的因素有很多,那么,在那么多的因素之中,肯定有几项因素比较重要,有几项相对不那么重要,我们暂时将每个因素的重要程度用一个数值来表示,可以近似理解为权重,然后将每个权重和因素的数值相乘相加,最后再加上一个常数项,那么这个式子就可以理解为一个回归方程。
1.2 SSE,SST和SSR
有了上述的基础,我们就可以做这样一件事,预先设定好一个方程(先简单一点,假设该方程只有一个自变量):y = ax + b,a和b是我们要求出来的;那么,我们可不可以这样理解,每输入一个x,即能通过这个计算式输出一个结果y,如果输出的y和真实的y偏差是最小的,那么不就能说明这个方程拟合的是最佳的了吗?顺着这个思路,原问题就可以演变成一个求解当a和b各为多少时能使得这个偏差值最小的求最优化问题了,或者说我们的目标就是求使得SSE最小的a和b的值。于是乎,SSE这个概念由此得来:SSE的英文全称为Sum Squared Error,误差平方和,它在数值上等于预测值减去真实值的平方和,计算公式为:
既然都已经价绍SSE了,我们就把另外两个成员也一并介绍了吧,先是SST,Sum Squared Total,总平方和,它在数值上等于真实值减去真实值的均值的平方和,注意不是方差!计算公式为:
再是SSR,Sum Squared Regression,回归平方和,它在数值上等于预测值减去真实值均值的平方和,计算公式为:
三者在数值上存在这样的关系:
1.3 R-Square及其他评估指标
经过上述公式的介绍,其实可以大致感觉到,SSE值越小则说明回归方程拟合得越好,但是到底要多小,小到什么程度才算比较好呢。比如,我们计算出来SSE等于10000,足够大了,但是我们并不能说这个方程拟合得不好,因为有可能,我们面对的数据量是100000000,相对这个数据量,10000的SSE绝对不能说不好。因此,我们在制定指标衡量模型拟合好坏时就必须将原始数据的因素考虑进去,于是乎,出现了我们常说的r平方,即R-Square指标,计算公式为:
有上述公式可知,SST是由原始数据得出的,因此可以看成是一个定值,SSE越小,模型拟合度越高,R-Square就越接近于1,反之,SSE越大,R-Square越接近于0,则说明模型解释性越差,由于R-Sqare在数值上是介于0和1之间的,因此我们可以很明确的知道模型的拟合得到底是好还是不好。
当然,除了R-Square之外,还有其他好几个指标也能够评价一个回归方程拟合的好坏,这里也简单地介绍一下:
MSE(Mean Squared Error):均方误差
可以理解为就是SSE除了一个样本数,计算公式为:
RMSE(Root Mean Squared Error):均方根误差
就是给均方误差开了一个根号,计算公式为:
MAE(平均绝对误差):平均绝对误差
计算的不再是平方和,而是绝对值之和,有点类似于曼哈顿距离和欧式距离之间的区别,计算公式为:
2. 二维平面内求解最小二乘法
2.1 假设条件及问题描述
设在一个直角坐标平面内,最优直线方程为:![]() ,为简化后续书写步骤,之后会一律表示为
,为简化后续书写步骤,之后会一律表示为 ![]() ,将该直角坐标平面上的一系列的点,
,将该直角坐标平面上的一系列的点,![]() 代入到SSE的计算公式:
代入到SSE的计算公式: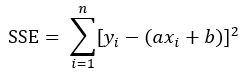 ,现求解a和b的值,使得SSE能取到最小值。
,现求解a和b的值,使得SSE能取到最小值。
2.2 计算过程详解
2.2.1 SSE图像形状
由SSE的计算式可知,该式可以表示的一般形式为:![]() ,这样的函数可以由基本函数
,这样的函数可以由基本函数![]() 进行一系列的拉伸平移等等的变换得到,研究该图像的形状,可知在三维空间中它是一个开口向上的抛物面,是一个凸函数,因此SSE必定可以取到最小值
进行一系列的拉伸平移等等的变换得到,研究该图像的形状,可知在三维空间中它是一个开口向上的抛物面,是一个凸函数,因此SSE必定可以取到最小值
2.2.2 求导,联立方程组并求解
下一步就比较简单了,对于这个方程,我们分别对a和b求偏导数,然后再联立方程组将a和b求解出来即可
将SSE表示成关于a的表达式(即将b看作常量),可得:
将SSE表示成关于b的表达式(即将a看作常量),可得:
将SSE分别对a和b求偏导数,得:
注意到该式分子分母都有1/n2,将1/n2 = 1/n * 1/n进行分配并表示成期望的形式,最终可将a的表达式变形为:
以上,二维平面内的回归方程的表达式求解步骤宣告完成!
3. 高维空间内求解最小二乘法
现在开始对原问题进行深入,现实情况错综复杂,如果需要用一个回归方程来解释某种现象,自变量的数量往往会有很多个,那这样,为求解出回归方程所需要用到的点组成的空间就必定是一个高维空间了,此时,需要使用到线性代数中的矩阵运算,现在开始求解这个方程的各项系数组成的矩阵
3.1 假设条件及问题描述
现将原问题扩展到p维空间,样本数量为n,将这些样本全部进行联立,并设置截距项组成一个多元方程组:
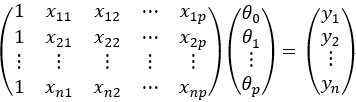
用线性代数中矩阵的思想将上式表示成矩阵相乘的形式,可得:
原式就变成了 ![]() ,现在,我们开始求解SSE,可得:
,现在,我们开始求解SSE,可得:
注意:上述求解过程利用到了矩阵转置公式 ![]()
3.2 计算过程详解
我们首先将SSE展开,可得:
![]()
对该式进行适当简单整理,可得:
![]()
观察上式,注意到该式的第二以及第三项经过矩阵运算过后的结果均为一个数字,该数字正好等于 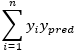 ,因此上式就可以进一步简化为:
,因此上式就可以进一步简化为:
![]()
对SSE求导,并令它的导数为0,可得(此处用到了矩阵求导方面的知识点,本人也还未对其进行深入的研究,对此有兴趣的朋友可以深入了解一下):
![]()
以上,矩阵A的求解过程宣告完成!
3.3 注意事项
由于A式包含逆矩阵,因此在使用该算法之前必须先计算XTX的行列式的值并判断其是否满秩,若XTX中的行或列存在线性相关,就无法运用该算法,这时,就需要用到Ridge或是Lasso算法来优化该模型,该知识点会在之后的博客中介绍。
4. 逐步回归算法
接下来介绍逐步回归算法,之前我们讲到的算法是根据公式推导直接得到最终结果的,而逐步回归算法则是通过反复地迭代一步一步将结果优化,最终得到一个最优结果,其基本思路如下:
(1). 原方程组可以表示成:
(2). 现对![]() 到
到![]() 这 p + 1 个元素进行迭代,每次迭代时,保持其他元素不变,而只变化当前元素,变化方式为预先设置一个lambda值,将当前元素加上这个lambda以及减去这个lambda各计算一次SSE,取两个SSE中的较小值,然后求得所有 p + 1 个元素的SSE的最小值,改变该元素的值即可,以上完成了一次迭代
这 p + 1 个元素进行迭代,每次迭代时,保持其他元素不变,而只变化当前元素,变化方式为预先设置一个lambda值,将当前元素加上这个lambda以及减去这个lambda各计算一次SSE,取两个SSE中的较小值,然后求得所有 p + 1 个元素的SSE的最小值,改变该元素的值即可,以上完成了一次迭代
(3). 将上述过程循环进行很多次,不断地迭代之后能够得到最优值
该算法具有一个一步步迭代的思想,由此可以引申到另一个机器学习领域中重要的算法:梯度下降法,这会在接下来的博客中进行总结。
5. 回归算法的代码实现
将上述算法使用python代码实现写成包如下:
import numpy as np import pandas as pd class regression: def __init__(self, data, intercept = True): self.X = np.mat(data.iloc[:,:-1].values) self.Y = np.mat(data.iloc[:,-1].values).T self.data = data self.intercept = intercept def basicfit(self): #This function aims to realize the basic linear regression algorithm if self.intercept == False: XTX = self.X.T * self.X if np.linalg.det(XTX) != 0: return np.ravel(XTX.I * self.X.T * self.Y) return ones = np.array([1] * self.data.shape[0]) self.X = np.mat(np.column_stack((ones, self.X))) XTX = self.X.T * self.X if np.linalg.det(XTX) == 0: print("linear dependent columns exist!!!") return return np.ravel(XTX.I * self.X.T * self.Y) def cal_SSE(self, theta): #This function aims to calculate the SSE value from a given theta Y_pred = self.X * np.mat(theta).T return np.power(self.Y - Y_pred, 2).sum() def stepfit(self, lam, iternum): #This function aims to realize the step linear regression algorithm theta = np.zeros(self.X.shape[1]) for _ in range(iternum): L = [] for i in range(len(theta)): v_plus = theta[i] + lam v_minus = theta[i] - lam theta[i] = v_plus SSE_plus = self.cal_SSE(theta) theta[i] = v_minus SSE_minus = self.cal_SSE(theta) L_tmp = [(SSE_plus, v_plus, i), (SSE_minus, v_minus, i)] L_tmp.sort() L.append(L_tmp[0]) L.sort() theta[L[0][2]] = L[0][1] return thetadef evaluate(self, coef): #This function aims to calculate SSE and R2 in order to evaluate whether the model is accurate or not Y_pred = self.X * np.mat(coef).T SSE = np.power(np.ravel(self.Y) - np.ravel(Y_pred), 2).sum() SST = np.power(np.ravel(self.Y) - np.ravel(self.Y).mean(), 2).sum() R2 = 1 - SSE / SST return SSE, R2