最近发生了一个报错:qt.network.ssl:QSslSocket::connectToHostEncrypted:TLSinitializationfailed//获取Qt所支持的版本qDebug()<<"OpenSSL支持的版本:"<
org.apache.flink.runtime.client.JobInitializationException: Could not start the JobMaster.
ForwardSummer
Error集锦大数据JVMjavajvmflink
IDEA执行Flink的类的main方法时,遇到如下错误,还以为是啥大错误,没想到只是路径错了,txt的文件格式没有拼全,加上txt就好了。Exceptioninthread"main"java.lang.RuntimeException:java.util.concurrent.ExecutionException:java.lang.RuntimeException:org.apache.fl
C语言读取 ini 配置文件,修改/添加键值对
Oliver-H
C_C++windowsc语言
C语言读取ini配置文件,修改/添加键值对C语言读取ini配置文件,对section中的键值对进行修改/添加,如果section不存在,则在末尾将新的section/key/value添加进去。一、了解什么是INI文件?ini文件是InitializationFile的缩写,即初始化文件,这是用来配置应用软件以实现不同用户的要求。二、INI文件的格式INI文件由节、键、值组成。一个简单的的INI文
C#性能优化技巧:利用Lazy<T>实现集合元素的延迟加载
AitTech
C#c#windows开发语言
一、C#中的LazyC#中的Lazy是一个泛型类,它实现了延迟加载(LazyInitialization)的功能。延迟加载是指对象的创建被推迟,直到第一次被使用时才进行实例化。这对于大型或资源密集型对象的性能优化非常有用,因为它可以避免不必要的初始化和资源消耗。二、Lazy与集合结合使用实现延迟加载Lazy可以与集合结合使用,以实现集合元素的延迟加载。这通常用于那些初始化代价较高或不需要立即初始化
Jmeter进阶篇(33)报错Error occurred during initialization of VM Could not reserve enough space…的解决方案
綦枫Maple
Jmeter性能测试大全jmeter
报错现象在使用Jmeter进行性能测试等操作时,可能会遇到各种各样的问题,其中一个比较常见的报错是在启动Jmeter的时候出现:ErroroccurredduringinitializationofVMCouldnotreserveenoughspacefor1048576KBobjectheaperrorlevel=1请按任意键继续...这个报错可能会让不少新手感到困惑,甚至会影响到性能测试工作
wandb超算运行的问题
ajin_97
python深度学习pytorch
wandb:Networkerror(ConnectionError),enteringretryloop.wandb:ERRORRuninitializationhastimedoutafter90.0sec.这是因为wandb需要联网运行,超算无法联网关闭wandb或者wandb设置为offline模式即可importosimportwandbos.environ["WANDB_API_KEY
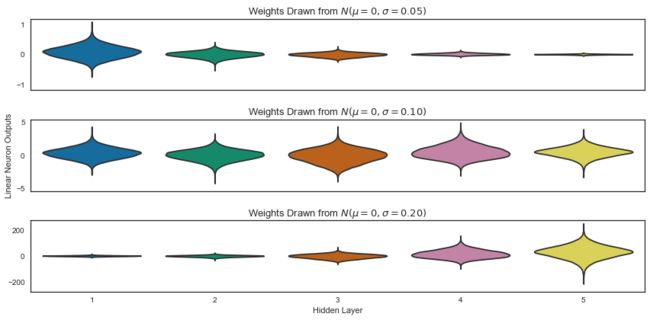
神经网络初始化 (init) 介绍
迷路爸爸180
神经网络人工智能深度学习初始化init
文章目录引言1.初始化的重要性1.1打破对称性1.2控制方差1.3加速收敛与提高泛化能力2.常见的初始化方法及其应用场景2.1Xavier/Glorot初始化2.2He初始化2.3正交初始化2.4其他初始化方法3.如何设置初始化4.基于BERT的文本分类如何进行初始化4.1项目背景4.2模型构建4.3模型训练与评估4.4结果分析结论参考资料引言在深度学习的世界中,构建一个高效且性能优异的神经网络模
HiveMetaException: Unknown version specified for initialization: 3.1.0(或者其他版本号)
一品_人生
mysqlhive大数据
遇到这个问题,也是很难发现的,查阅很多文章,乱七八糟,也可能是遇到的问题不相同吧,我们从以下两个方面去排查吧1.检查你的hive-site.xml和hive-env.sh,配置对就行,这个网上一大片,注意要正确。2.那就是你解压的hive压缩文件,然后发现要安装mysql,这时你会先检查你本地有没有mysql,使用find/-namemysql(罪源),然后你就一通删除,你没有发现你删除了一个hi
记录 io.springfox 3.0.0 整合 spring boot 2.6.x 由于 springfox bug 引发问题
树懒_Zz
Springspringbootbugwindows
首先第一个问题就是不兼容:解决方案:@BeanpublicstaticBeanPostProcessorspringfoxHandlerProviderBeanPostProcessor(){returnnewBeanPostProcessor(){@OverridepublicObjectpostProcessAfterInitialization(Objectbean,StringbeanNa
CSV文件转换coe
一条九漏鱼
matlabfpga开发matlab
CodeN=165;y=zeros(N,1);%unzip('Under_A.ila')A=importdata('Control_txA.csv');fid=fopen('demo.coe','wt');%-standardformatfprintf(fid,'MEMORY_INITIALIZATION_RADIX=16;\n');fprintf(fid,'MEMORY_INITIALIZATI
2011寒假-数据库学习笔记
weixin_33967071
数据库设计模式人工智能
第一课:数据库类型1.1平面文件适用于:1,数值小且简单2,数值不经常变化3,希望能够使用简单的文本编辑器来更改数值4,希望保存以前数值的简单历史清单,5,希望使用工具快速比较两个文件例如:INI文件(initialization)1.2关系数据库适用于:l需要在不同的表之间执行复杂的查询和连接.l需要执行数据有效性验证,如在其他表中检验相关行的存在.l需要为特定的数据有效性验证,如在其他表中检验
C++单例模式的设计
Alvin's Tech Blog
C/C++学习单例模式c++开发语言
单例模式(SingletonPattern)是一种设计模式,用于确保一个类只有一个实例,并提供一个全局访问点来访问该实例。在C++中,单例模式通常用于管理全局资源或共享状态。以下是C++中实现单例模式的几种常见方式:懒汉式(LazyInitialization)懒汉式单例在第一次使用时才创建实例。非线程安全版本:classSingleton{public:staticSingleton&getIn
npm dev时遇到错误“error:0308010C:digital envelope routines::unsupported“的解决办法
_Eolin
npm前端node.js
报错:opensslErrorStack:['error:03000086:digitalenveloperoutines::initializationerror'], library:'digitalenveloperoutines', reason:'unsupported', code:'ERR_OSSL_EVP_UNSUPPORTED'顺便看了一下错误堆栈,发现是一个Node的内核文件抛
C++——智能指针
很楠不爱
c++开发语言
前言:哈喽小伙伴们,今天我们继续来分享C++的一个全新知识——智能指针。目录一.何为智能指针RAII二.智能指针的种类三.内存泄漏结语一.何为智能指针RAIIRAII(ResourceAcquisitionIsInitialization)是一种利用对象生命周期来控制程序资源(如内存、文件句柄、网络连接、互斥量等等)的简单技术。在对象构造时获取资源,接着控制对资源的访问使之在对象的生命周期内始终保
Spring Boot启动卡在Root WebApplicationContext: initialization completed in...
江湖一码农
springboot后端javamysql
SpringBoot启动打印RootWebApplicationContext:initializationcompletedin...这行日志完成后需要等很长时间才能真正启动完成。分析一下发现是连接某个机器的MySQL就会出现这种情况。使用客户端软件连接MySQL时也很慢,但连接完成后执行MySQL各种语句非常看。查看MySQL链接时,发现所有的链接都会出现unauthenticateduser
设计模式 —— 单例模式
idealzouhu
设计模式设计模式单例模式
文章目录一、单例模式1.1单例模式定义1.2单例模式的优点1.3单例模式的缺点1.4单例模式的使用场景二、普通案例2.1饿汉式单例模式(EagerInitializationSingleton)2.2懒汉式单例模式(LazyInitializationSingleton)参考资料本文源代码地址为java-demos/singeleton-patternatmain·idealzouhu/java-
对Vue组件生命周期的理解
2401_85770776
vuevue.js前端javascript
Vue.js组件生命周期中的几个重要阶段:创建、初始化数据、编译模板、挂载DOM、更新渲染、卸载。这些阶段对应了Vue.js的生命周期钩子函数。下面我将详细解释每个阶段以及它们在Vue.js生命周期中的作用。文章目录1.创建(Creation)2.初始化数据(InitializationofData)3.编译模板(TemplateCompilation)4.挂载DOM(MountingtheDOM
iniparser 使用方法介绍
kunsir_
iniparserlinux嵌入式
一、iniparser的概述INI(InitializationFile)文件是一种简单直观的数据存储格式,常用于配置应用程序的初始化设置。这种文件通常包含若干个节(section)和键值对(key-valuepairs)。INI文件的每一部分都是自描述性的,易于阅读和编辑,使得非程序员也能轻易理解并修改配置参数。INI文件因其简单易用性而在许多编程语言中广泛应用,尤其是在Windows操作系统中
使用C++开发黑神话悟空类似3A如何避免内存泄漏
Code apprenticeship
后端c++java开发语言
智能指针:使用C++11或更高版本中的智能指针(如std::unique_ptr、std::shared_ptr和std::weak_ptr)来自动管理内存。这些智能指针在超出作用域时会自动释放它们所管理的内存。RAII(ResourceAcquisitionIsInitialization):采用RAII原则,确保资源在对象生命周期结束时被正确释放。这意味着资源的获取和释放与对象的创建和销毁同步
Spring IOC 创建Bean过程
学博成
框架Spring
ABC.class---推断构造涵数-->createInstance(普通对象)-->依赖注入字段、属性-->Aware(设置Bean名称)-->初始化InitializingBean【voidafterPropertiesSet()】回调-->BeanPostProcessor(AOP)后置处理初始化之前:ObjectpostProcessBeforeInitialization(Object
mongodb 在 Ubuntu系统上的安装及卸载
weixin_30892889
数据库嵌入式
mongodb官网Themongodb-org-serverpackageprovidesaninitializationscriptthatstartsmongodwiththe/etc/mongod.confconfigurationfile.SeeRunMongoDBCommunityEditionfordetailsonusingthisinitializationscript.These
Java中的单例模式
士伟丷
设计模式java单例模式
单例模式(SingletonPattern)本身并不是不安全的,但是它在多线程环境中的实现如果不正确,则可能会导致线程安全问题。单例模式的主要目的是确保一个类只有一个实例,并提供一个全局访问点来获取该实例。在Java中,实现线程安全的单例模式通常有几种方法:懒汉式(LazyInitialization)双重检查锁定(Double-CheckedLocking):这是一种常见的实现方式,通过双重检查
Go 语言范围(Range) 16
寂然如故
GO语言入门golangjava前端
在Go语言中,范围(Range)是一种语法结构,用于遍历切片、数组、字符串、map等数据结构中的值。范围语法结构通常用于遍历数据结构中的每个值,并对其进行处理。范围语法范围语法结构的基本形式是:forinitialization;condition;post{//代码块}其中:initialization:初始化语句,用于设置范围的起始值。condition:条件语句,用于判断是否继续遍历范围。p
解线性方程组
qiuwanchi
package gaodai.matrix;
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Test {
public static void main(String[] args) {
Scanner scanner = new Sc
在mysql内部存储代码
annan211
性能mysql存储过程触发器
在mysql内部存储代码
在mysql内部存储代码,既有优点也有缺点,而且有人倡导有人反对。
先看优点:
1 她在服务器内部执行,离数据最近,另外在服务器上执行还可以节省带宽和网络延迟。
2 这是一种代码重用。可以方便的统一业务规则,保证某些行为的一致性,所以也可以提供一定的安全性。
3 可以简化代码的维护和版本更新。
4 可以帮助提升安全,比如提供更细
Android使用Asynchronous Http Client完成登录保存cookie的问题
hotsunshine
android
Asynchronous Http Client是android中非常好的异步请求工具
除了异步之外还有很多封装比如json的处理,cookie的处理
引用
Persistent Cookie Storage with PersistentCookieStore
This library also includes a PersistentCookieStore whi
java面试题
Array_06
java面试
java面试题
第一,谈谈final, finally, finalize的区别。
final-修饰符(关键字)如果一个类被声明为final,意味着它不能再派生出新的子类,不能作为父类被继承。因此一个类不能既被声明为 abstract的,又被声明为final的。将变量或方法声明为final,可以保证它们在使用中不被改变。被声明为final的变量必须在声明时给定初值,而在以后的引用中只能
网站加速
oloz
网站加速
前序:本人菜鸟,此文研究总结来源于互联网上的资料,大牛请勿喷!本人虚心学习,多指教.
1、减小网页体积的大小,尽量采用div+css模式,尽量避免复杂的页面结构,能简约就简约。
2、采用Gzip对网页进行压缩;
GZIP最早由Jean-loup Gailly和Mark Adler创建,用于UNⅨ系统的文件压缩。我们在Linux中经常会用到后缀为.gz
正确书写单例模式
随意而生
java 设计模式 单例
单例模式算是设计模式中最容易理解,也是最容易手写代码的模式了吧。但是其中的坑却不少,所以也常作为面试题来考。本文主要对几种单例写法的整理,并分析其优缺点。很多都是一些老生常谈的问题,但如果你不知道如何创建一个线程安全的单例,不知道什么是双检锁,那这篇文章可能会帮助到你。
懒汉式,线程不安全
当被问到要实现一个单例模式时,很多人的第一反应是写出如下的代码,包括教科书上也是这样
单例模式
香水浓
java
懒汉 调用getInstance方法时实例化
public class Singleton {
private static Singleton instance;
private Singleton() {}
public static synchronized Singleton getInstance() {
if(null == ins
安装Apache问题:系统找不到指定的文件 No installed service named "Apache2"
AdyZhang
apachehttp server
安装Apache问题:系统找不到指定的文件 No installed service named "Apache2"
每次到这一步都很小心防它的端口冲突问题,结果,特意留出来的80端口就是不能用,烦。
解决方法确保几处:
1、停止IIS启动
2、把端口80改成其它 (譬如90,800,,,什么数字都好)
3、防火墙(关掉试试)
在运行处输入 cmd 回车,转到apa
如何在android 文件选择器中选择多个图片或者视频?
aijuans
android
我的android app有这样的需求,在进行照片和视频上传的时候,需要一次性的从照片/视频库选择多条进行上传
但是android原生态的sdk中,只能一个一个的进行选择和上传。
我想知道是否有其他的android上传库可以解决这个问题,提供一个多选的功能,可以使checkbox之类的,一次选择多个 处理方法
官方的图片选择器(但是不支持所有版本的androi,只支持API Level
mysql中查询生日提醒的日期相关的sql
baalwolf
mysql
SELECT sysid,user_name,birthday,listid,userhead_50,CONCAT(YEAR(CURDATE()),DATE_FORMAT(birthday,'-%m-%d')),CURDATE(), dayofyear( CONCAT(YEAR(CURDATE()),DATE_FORMAT(birthday,'-%m-%d')))-dayofyear(
MongoDB索引文件破坏后导致查询错误的问题
BigBird2012
mongodb
问题描述:
MongoDB在非正常情况下关闭时,可能会导致索引文件破坏,造成数据在更新时没有反映到索引上。
解决方案:
使用脚本,重建MongoDB所有表的索引。
var names = db.getCollectionNames();
for( var i in names ){
var name = names[i];
print(name);
Javascript Promise
bijian1013
JavaScriptPromise
Parse JavaScript SDK现在提供了支持大多数异步方法的兼容jquery的Promises模式,那么这意味着什么呢,读完下文你就了解了。
一.认识Promises
“Promises”代表着在javascript程序里下一个伟大的范式,但是理解他们为什么如此伟大不是件简
[Zookeeper学习笔记九]Zookeeper源代码分析之Zookeeper构造过程
bit1129
zookeeper
Zookeeper重载了几个构造函数,其中构造者可以提供参数最多,可定制性最多的构造函数是
public ZooKeeper(String connectString, int sessionTimeout, Watcher watcher, long sessionId, byte[] sessionPasswd, boolea
【Java命令三】jstack
bit1129
jstack
jstack是用于获得当前运行的Java程序所有的线程的运行情况(thread dump),不同于jmap用于获得memory dump
[hadoop@hadoop sbin]$ jstack
Usage:
jstack [-l] <pid>
(to connect to running process)
jstack -F
jboss 5.1启停脚本 动静分离部署
ronin47
以前启动jboss,往各种xml配置文件,现只要运行一句脚本即可。start nohup sh /**/run.sh -c servicename -b ip -g clustername -u broatcast jboss.messaging.ServerPeerID=int -Djboss.service.binding.set=p
UI之如何打磨设计能力?
brotherlamp
UIui教程ui自学ui资料ui视频
在越来越拥挤的初创企业世界里,视觉设计的重要性往往可以与杀手级用户体验比肩。在许多情况下,尤其对于 Web 初创企业而言,这两者都是不可或缺的。前不久我们在《右脑革命:别学编程了,学艺术吧》中也曾发出过重视设计的呼吁。如何才能提高初创企业的设计能力呢?以下是 9 位创始人的体会。
1.找到自己的方式
如果你是设计师,要想提高技能可以去设计博客和展示好设计的网站如D-lists或
三色旗算法
bylijinnan
java算法
import java.util.Arrays;
/**
问题:
假设有一条绳子,上面有红、白、蓝三种颜色的旗子,起初绳子上的旗子颜色并没有顺序,
您希望将之分类,并排列为蓝、白、红的顺序,要如何移动次数才会最少,注意您只能在绳
子上进行这个动作,而且一次只能调换两个旗子。
网上的解法大多类似:
在一条绳子上移动,在程式中也就意味只能使用一个阵列,而不使用其它的阵列来
警告:No configuration found for the specified action: \'s
chiangfai
configuration
1.index.jsp页面form标签未指定namespace属性。
<!--index.jsp代码-->
<%@taglib prefix="s" uri="/struts-tags"%>
...
<s:form action="submit" method="post"&g
redis -- hash_max_zipmap_entries设置过大有问题
chenchao051
redishash
使用redis时为了使用hash追求更高的内存使用率,我们一般都用hash结构,并且有时候会把hash_max_zipmap_entries这个值设置的很大,很多资料也推荐设置到1000,默认设置为了512,但是这里有个坑
#define ZIPMAP_BIGLEN 254
#define ZIPMAP_END 255
/* Return th
select into outfile access deny问题
daizj
mysqltxt导出数据到文件
本文转自:http://hatemysql.com/2010/06/29/select-into-outfile-access-deny%E9%97%AE%E9%A2%98/
为应用建立了rnd的帐号,专门为他们查询线上数据库用的,当然,只有他们上了生产网络以后才能连上数据库,安全方面我们还是很注意的,呵呵。
授权的语句如下:
grant select on armory.* to rn
phpexcel导出excel表简单入门示例
dcj3sjt126com
PHPExcelphpexcel
<?php
error_reporting(E_ALL);
ini_set('display_errors', TRUE);
ini_set('display_startup_errors', TRUE);
if (PHP_SAPI == 'cli')
die('This example should only be run from a Web Brows
美国电影超短200句
dcj3sjt126com
电影
1. I see. 我明白了。2. I quit! 我不干了!3. Let go! 放手!4. Me too. 我也是。5. My god! 天哪!6. No way! 不行!7. Come on. 来吧(赶快)8. Hold on. 等一等。9. I agree。 我同意。10. Not bad. 还不错。11. Not yet. 还没。12. See you. 再见。13. Shut up!
Java访问远程服务
dyy_gusi
httpclientwebservicegetpost
随着webService的崛起,我们开始中会越来越多的使用到访问远程webService服务。当然对于不同的webService框架一般都有自己的client包供使用,但是如果使用webService框架自己的client包,那么必然需要在自己的代码中引入它的包,如果同时调运了多个不同框架的webService,那么就需要同时引入多个不同的clien
Maven的settings.xml配置
geeksun
settings.xml
settings.xml是Maven的配置文件,下面解释一下其中的配置含义:
settings.xml存在于两个地方:
1.安装的地方:$M2_HOME/conf/settings.xml
2.用户的目录:${user.home}/.m2/settings.xml
前者又被叫做全局配置,后者被称为用户配置。如果两者都存在,它们的内容将被合并,并且用户范围的settings.xml优先。
ubuntu的init与系统服务设置
hongtoushizi
ubuntu
转载自:
http://iysm.net/?p=178 init
Init是位于/sbin/init的一个程序,它是在linux下,在系统启动过程中,初始化所有的设备驱动程序和数据结构等之后,由内核启动的一个用户级程序,并由此init程序进而完成系统的启动过程。
ubuntu与传统的linux略有不同,使用upstart完成系统的启动,但表面上仍维持init程序的形式。
运行
跟我学Nginx+Lua开发目录贴
jinnianshilongnian
nginxlua
使用Nginx+Lua开发近一年的时间,学习和实践了一些Nginx+Lua开发的架构,为了让更多人使用Nginx+Lua架构开发,利用春节期间总结了一份基本的学习教程,希望对大家有用。也欢迎谈探讨学习一些经验。
目录
第一章 安装Nginx+Lua开发环境
第二章 Nginx+Lua开发入门
第三章 Redis/SSDB+Twemproxy安装与使用
第四章 L
php位运算符注意事项
home198979
位运算PHP&
$a = $b = $c = 0;
$a & $b = 1;
$b | $c = 1
问a,b,c最终为多少?
当看到这题时,我犯了一个低级错误,误 以为位运算符会改变变量的值。所以得出结果是1 1 0
但是位运算符是不会改变变量的值的,例如:
$a=1;$b=2;
$a&$b;
这样a,b的值不会有任何改变
Linux shell数组建立和使用技巧
pda158
linux
1.数组定义 [chengmo@centos5 ~]$ a=(1 2 3 4 5) [chengmo@centos5 ~]$ echo $a 1 一对括号表示是数组,数组元素用“空格”符号分割开。
2.数组读取与赋值 得到长度: [chengmo@centos5 ~]$ echo ${#a[@]} 5 用${#数组名[@或
hotspot源码(JDK7)
ol_beta
javaHotSpotjvm
源码结构图,方便理解:
├─agent Serviceab
Oracle基本事务和ForAll执行批量DML练习
vipbooks
oraclesql
基本事务的使用:
从账户一的余额中转100到账户二的余额中去,如果账户二不存在或账户一中的余额不足100则整笔交易回滚
select * from account;
-- 创建一张账户表
create table account(
-- 账户ID
id number(3) not null,
-- 账户名称
nam