2.1.2回归预测
回归问题和分类问题的区别在于:其待预测的目标是连续变量,比如:价格、降水量等等。
2.1.2.1线性回归器
模型介绍:在“2.1.1.1线性分类器“节中,重点介绍了用于分类的线性模型。其中为了便于将原本在实数域上的计算结果映射到(0,1)区间,引入了逻辑斯蒂函数。而在线性回归问题中,由于预测目标直接是实数域上的数值,因此优化目标就更为简单,即最小化预测结果与真实值之间的差异。
美国波士顿地区房价数据描述
from sklearn.datasets import load_boston
#从读取房价数据存储在变量boston中。
boston=load_boston()
#输出数据描述
print(boston.DESCR)
该数据共有506条,每条数据包括对指定房屋的13项数值型特征描述和目标房价。另外,该数据中没有缺失的属性/特征值,更加方便了后续分析。
美国波士顿地区房价数据分割
from sklearn.cross_validation import train_test_split
import numpy as np
X=boston.data
y=boston.target
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.25,random_state=33)
#分析回归目标值的差异
print('The max target value is',np.max(boston.target))
print('The max target value is',np.min(boston.target))
print('The max target value is',np.mean(boston.target))
The max target value is 50.0
The max target value is 5.0
The max target value is 22.5328063241
经初步查验,预测目标房价之间的差异较大,因此需要对特征以及目标值进行标准化处理。
训练与测试数据标准化处理
from sklearn.preprocessing import StandardScaler
#分别初始化对特征和目标值的标准化器
ss_X=StandardScaler()
ss_y=StandardScaler()
#分别对训练和测试数据的特征以及目标值进行标准化处理
X_train=ss_X.fit_transform(X_train)
X_test=ss_X.fit_transform(X_test)
y_train=ss_y.fit_transform(y_train)
y_test=ss_y.fit_transform(y_test)
使用线性回归模型LinearRegression和SGDRegressor分别对美国波士顿地区房价进行预测
from sklearn.linear_model import LinearRegression
#使用默认配置初始化线性回归器LinearRegression
lr=LinearRegression()
#使用训练数据进行参数估计
lr.fit(X_train,y_train)
#对测试数据进行回归预测。
lr_y_predict=lr.predict(X_test)
from sklearn.linear_model import SGDRegressor
#使用默认配置初始化线性回归器SGDRegressor
sgdr=SGDRegressor()
sgdr.fit(X_train,y_train)
sgdr_y_predict=sgdr.predict(X_test)
不同于类别预测,我们不能苛求回归预测的数值结果要严格地与真实值相同。一般情况下,我们希望衡量预测值与真实值之间的差距。因此,可以通过多种测评函数进行评价。其中最为直观的评价指标包括,平均绝对误差(Mean Absolute Error,MAE)以及均方误差(Mean Squared Error,MSE),因为这也是线性回归模型所要优化的目标。
R-squared用来衡量模型回归结果的波动可被真实值验证的百分比,也暗示模型在数值回归方面的能力。
使用三种回归评价机制以及两种调用R-squared评价模块的方法,对本节模型的回归性能做出评价
print('The value of default measurement of LinearRegression is',lr.score(X_test,y_test))
#回归性能的评估
from sklearn.metrics import r2_score,mean_squared_error,mean_absolute_error
#使用r2_score模块,并输出评估结果
print('The value of R-squared error of LinearRegression is',r2_score(y_test,lr_y_predict))
#使用mean_squared_error模块,并输出评估结果
print('The mean_squared_error of LinearRegression is',mean_squared_error(ss_y.inverse_transform(y_test),ss_y.inverse_transform(lr_y_predict)))
#使用mean_absolute_error模块,并输出评估结果
print('The mean_absolute_error of LinearRegression is',mean_absolute_error(ss_y.inverse_transform(y_test),ss_y.inverse_transform(lr_y_predict)))
The value of default measurement of LinearRegression is 0.676930350524
The value of R-squared error of LinearRegression is 0.676930350524
The mean_squared_error of LinearRegression is 25.0512388542
The mean_absolute_error of LinearRegression is 3.51371562676
print('The value of default measurement of SGDRegressor is',sgdr.score(X_test,y_test))
#使用r2_score模块,并输出评估结果
print('The value of R-squared error of SGDRegressor is',r2_score(y_test,sgdr_y_predict))
#使用mean_squared_error模块,并输出评估结果
print('The mean_squared_error of SGDRegressor is',mean_squared_error(ss_y.inverse_transform(y_test),ss_y.inverse_transform(sgdr_y_predict)))
#使用mean_absolute_error模块,并输出评估结果
print('The mean_absolute_error of SGDRegressor is',mean_absolute_error(ss_y.inverse_transform(y_test),ss_y.inverse_transform(sgdr_y_predict)))
The value of default measurement of SGDRegressor is 0.655904035792
The value of R-squared error of SGDRegressor is 0.655904035792
The mean_squared_error of SGDRegressor is 26.6816465185
The mean_absolute_error of SGDRegressor is 3.51881056828
通过上面两段代码的输出,我们知道两种调用R-squared的方式是等价的。后续有关回归模型的评价,我们都会采用第一种方式,即回归模型自带的评估模块来完成性能的评估,另外,也可以看出三种评价方式R-squared、MSE以及MAE在具体评估结果上不同,但是在评价总体优劣程度上是一致的。
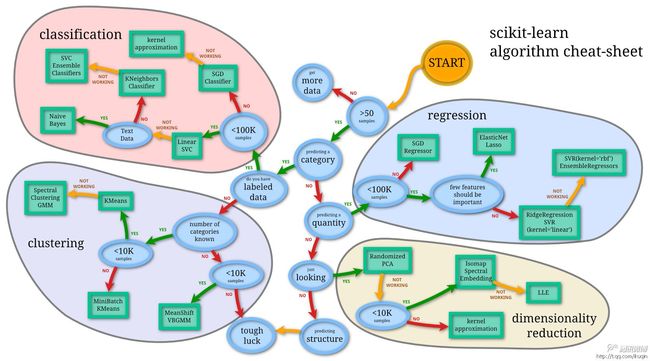
虽然,使用随机梯度下降估计参数的方法SGDRegressor在性能表现上不及使用解析方法的LinearRegression;但是如果面对训练数据规模十分庞大的任务,随机梯度法无论是在分类还是回归问题上都表现得十分高效,可以在不损失过多性能的前提下,节省大量计算时间。请读者在今后使用中,根据预测任务的数据规模,参考图片选择合适的模型。如果数据规模超过10万,推荐使用随机梯度法估计参数模型。
特点分析
线性回归器是最为简单、易用的回归模型。正是因为其对特征与回归目标之间的线性假设,从某种程度上说也局限了其应用范围。特别是,现实生活中的许多实例数据的各个特征与回归目标之间,绝大多数不能保证严格的线性关系。尽管如此,在不清楚特征之间关系的前提下,我们仍然可以使用线性回归模型作为大多数科学试验的基线系统。