第一次DS博客作业
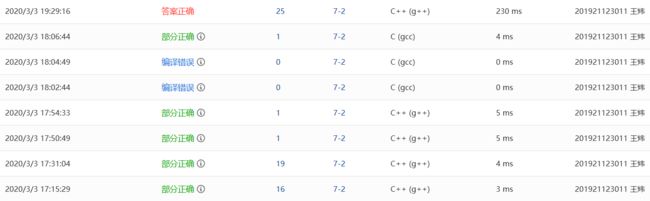
Q0.展示PTA总分
Q1.本章学习总结
1.1 学习内容总结
-
顺序表
-
顺序表和有序表？
- 顺序表和有序表都是以数组的形式保存的线性表，用一组地址连续的存储单元依次存储线性表中的各个元素。
- 其中，顺序表是指数据在存储位置上相邻，但数据值不一定递增或递减（例如某一数组储存的线性表1->5->2->4->3）
- 而有序表，就是数据元素按序排列，数据的值按递增或递减的关系储存顺序表（如1->2->3->4->5就是一个有序表）
- 因此可以说，有序表就是一种特殊的顺序表
-
顺序表的定义：结构体中一般包含两个内容，用于存储数据的数组和用于记录顺序表长度的一个变量，无特别内容
-
typedef struct List
{
ElemType data[MaxSize]; //ElemType代表该顺序表存储的数据类型，MaxSize代表顺序表元素最大数量
int length ; //记录顺序表的长度
} ;
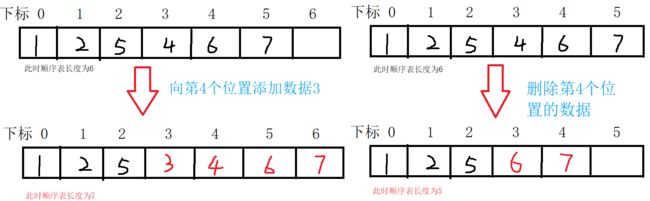
- 顺序表插入与删除：对于顺序表来说，插入或删除第i个位置的元素的操作较为简单，只需要对第i个位置之后的数组内容进行挪动（插入：右移，删除：左移）即可，但是要注意，这些操作结束之后要对顺序表的长度进行增减，同时最好要对输入的i进行验证，判断是不是合法的位置
for (int j = L->length; j >= i; j--) //插入
{
L->data[j] = L->data[j - 1]; //数组内元素右移
}
L->data[j] = x; //插入数据x
L->length++; //插入后顺序表长度+1
for (int j = i - 1; j < L->length - 1; j++) //删除
{
L->data[j] = L->data[j + 1]; //数组内元素左移，注意不要越界了
}
L->length--; //插入后顺序表长度-1
- 顺序表查找：由于是数组保存，查找第i个位置时我们可以直接通过下标来进行访问，同样注意对i进行验证；查找元素时则可以用遍历
/*查找位置，如找到返回该数值，否则返回-1*/
int Find1(int i, List L)
{
if(i <= 0 && i > L->length)
return -1;
else return L->data[i - 1];
}
/*查找元素，如找到返回该元素的下标，否则返回-1*/
int Find2(int i, List L)
{
for(int j = 0; j < L->length; j++)
if (L->data[j] == i)
return j;
return -1;
}
-
顺序表销毁：同样因为是数组，销毁的操作也很方便，只需要一句delete L即可，这里不做说明
-
链表
- 定义：链表是一种物理存储单元上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列结点组成，结点可以在运行时动态生成。每个结点包括两个部分：一个是存储数据元素的数据，另一个是存储下一个结点地址的指针。
typedef struct LNode //定义单链表结点类型
{
ElemType data;
struct LNode *next; //指向后继结点
} LNode,*LinkList;
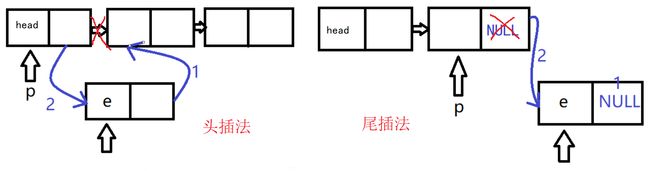
- 头插法与尾插法：头插法会使输入的数据插入到链表的表头，使输入数据的顺序与即为链表的倒序；尾插法使每次的数据插入到链尾，使输入数据的顺序与即为链表的顺序。使用哪一种方法建立链表要根据具体题目具体分析。以空链表分别用头插、尾插法按顺序添加新结点1、2、3为例，头插法为1、2->1、3->2->1，尾插法为1、1->2、1->2->3
void CreateListF(LinkList& L, int n) //头插法，n为数据个数
{
int i;
LinkList p;
L = new LNode;
L->next = NULL;
for (i = 0; i < n; i++)
{
p = new LNode;
cin >> p->data;
p->next = L->next; //这两句是关键。将原本头结点后面的所有结点保留
L->next = p; //让p作为头结点的next结点
}
}
void CreateListR(LinkList& L, int n) //尾插法
{
LinkList tail, p;
int i;
L = new LNode;
L->next = NULL;
tail = L; //尾插法需要一个尾指针
for (i = 0; i < n; i++)
{
p = new LNode;
cin >> p->data;
p->next = NULL; //这三句是关键。这句话在这里不要的话需要在插入完毕后tail->next=NULL;
tail->next = p; //尾指针的next结点为p结点
tail = p; //尾指针指向p结点
}
}
- 链表的插入与删除：链表不能利用下标直接访问，那么我们只能逐个结点进行访问，再进行插入和删除的操作，同样的要对i和结点位置进行判断，防止出现非法访问。一定要注意各个结点之间的关系，不要出现断链的情况，删除操作要记得释放删除结点的空间
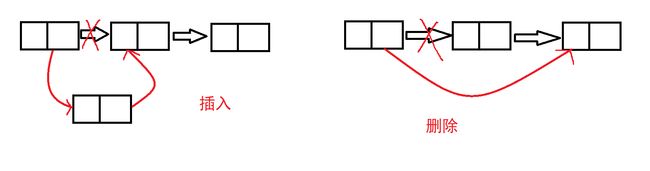
/*删除第i个位置的元素*/
bool DeleteList（LinkList head，int i）
{
ListNode* p，*r; //声明两个指针，p用来找到删除结点前的结点。r存储要删除结点的后继结点。
p = head;
int j = 1;
while(p->next && jnext
{
p=p->next;
j++;
}
if(p->next ==NULL || j>i) //找不到的情况
{
return false;
}
r=p->next; //这两句是重点。改变了原来链的关系
p->next=r->next; //相当于p->next=p->next->next
delete r; //释放结点
retuen true;
}
/*向第i个位置插入元素x*/
bool InsertList(LinkList head,ElemType x,int i)
{
ListNode* p;
p=head;
int j=1;
while(p && jnext;
j++;
}
if(!p || j>i) //找不到的情况
{
return false;
}
ListNode* s = new LNode;
s->data=x;
s->next=p->next //这两句是关键。先保留插入位置之后链表的关系
p->next=s; //然后再把该结点接入
return true;
}
- 查找：本质上还是对链表的遍历，查找第i个位置只需将链表从头节点向后遍历i次，查找元素的位置只需遍历链表寻找数据相符的元素，同时注意不要发生非法访问即可，大体上代码和插入删除的代码的循环部分相同，这里不再重复说明
- 销毁：链表的销毁，虽然我们平时在写程序中很少会在程序结束前将所有的链表销毁掉，但我们还是要知道这个东西的，毕竟一个很长的链表可能会占用很多内存。链表的销毁不能像数组那样一步到位，我们需要一个结点一个结点的进行删除
void DestroyList(LinkList &L)
{
LinkList p = L;
while (L)
{
p = L;
L = L->next;
delete p;
}
}
- 有序表的操作
- 插入
对于有序表的插入，我们常用下面的方法进行操作（以从小到大排序为例子），数组存储的：从头结点开始遍历-->找到第i个结点的数据大于需要插入的数据x-->从表的最后一个元素到第i个元素都向右移动一位-->将元素x插入到第i个位置-->有序表长度加1
对于链表存储的：从头结点开始遍历-->找到第i个结点的下一个结点的数据大于需要插入的数据x-->新建临时节点，在第i个结点进行插入操作
- 插入
/*数组*/
void InsertSq(SqList& L, int x)
{
int i;
for (i = 0; i < L->length; i++)
{
if (L->data[i] >= x)
{
for (int j = L->length; j > i; j--) //右移
L->data[j] = L->data[j - 1];
L->data[i] = x;
L->length++; //一定不能漏，因为插入了元素表长改变了
return;
}
}
L->data[L->length] = x; //插入到尾部的情况
L->length++;
}
/*链表*/
void ListInsert(LinkList& L, ElemType e)
{
LinkList p = L;
LinkList temp = new LNode;
while (p->next != NULL)
{
if (p->next->data > e)
break;
else
p = p->next;
}
temp->data = e;
temp->next = p->next;
p->next = temp;
}
- 删除
删除操作其实与插入操作大同小异，只有少许不同。数组存储的：从头结点开始遍历-->找到第i个结点的数据即为需要删除的数据x-->从表的第i个元素到length-1个元素全部左移一位-->有序表长度减1
对于链表存储的：从头结点开始遍历-->找到第i个结点的下一个结点的数据即为需要删除的数据x-->保存该结点，原结点的下一个结点链接到删除结点的下一个结点-->释放空间
/*数组*/
void DelNode(SqList& L, int x)
{
int i;
for (i = 0; i < L->length; i++)
{
if (L->data[i] == x)
{
L->length--; //删去一个元素，表长减一
for (int j = i; j < L->length; j++)
L->data[j] = L->data[j + 1];
return;
}
}
}
/*链表*/
void ListDelete(LinkList& L, ElemType e)
{
LinkList p = L;
LinkList temp = new LNode;
while (p->next != NULL)
{
if (p->next->data == e)
break;
else
p = p->next;
}
temp = p->next;
p->next = temp->next;
delete temp;
}
- 有序表合并
- 对于数组储存，可以通过新建一个数组，将数组A和数组B的元素逐个比较，若A的第i个元素大于B的第j个元素，则将B的第j个元素放入C中，j向后移动；若B的第j个元素大于A的第i个元素，则将A的第i个元素放入C中，i向后移动；若A的第i个元素与B的第j个元素相等，选取一个存入C中，i、j同时向后移动。若一个数组遍历完后，另一个数组还有剩余，则直接将剩余数组的内容插入到C的尾部
- 对于链表储存，可以通过上面的方法新建一条链表进行操作，也可以直接在其中的一条链上进行操作（因为不用再担心数组会越界的问题，并且如果另一表有剩余可以一步到位赋给原表）
void MergeList(LinkList& L1, LinkList L2) //两个链表合并
{
LinkList p1 = L1, p2 = L2;
LinkList temp;
while (1)
{
if (!p2->next)
break;
if (p1->data == p2->next->data) //已有数据跳过
{
p2 = p2->next;
continue;
}
if (p1->next == NULL && p2->next != NULL) //一表有剩余的情况
{
p1->next = p2->next;
break;
}
if (p1->next->data > p2->next->data) //使得合并后的表仍然有序排列
{
temp = new LNode;
temp->data = p2->next->data;
temp->next = p1->next;
p1->next = temp;
p2 = p2->next;
}
else
p1 = p1->next;
}
}
-
循环链表与双链表
- 循环链表
- 如图所见，循环链表与普通的单链表大同小异，只是尾指针的next又指向了头结点而已
- 所以十分简单我们可以知道，循环链表的创建只需要在创建完毕后在补上尾指针tail->next=head就可以了
- 通过循环链表，我们可以在链表的任何一个结点遍历整个链表了
- 循环链表为空的判断条件为head->next==head
- 双链表
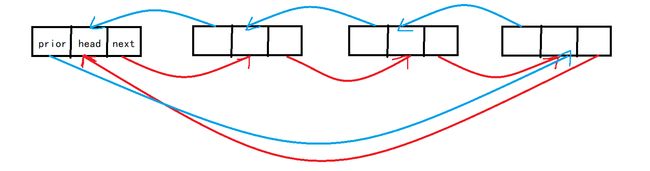
- 在单链表的基础上新增了一个prior的前驱指针，指向该结点的上一个结点，它同时也是循环链表
- 可以同时往两个方向遍历，循环结束的条件根据结点个数的奇偶不同
- 与创建普通链表需要添加：L->next=L->prior=L（初始化双向链表L时）
尾插法添加一个新结点时：tail->next = temp;（尾指针连向新结点） tail->next->prior = tail;（新结点的前驱指针等于当前结点） tail->next->next = L;（新的尾指针的下一节点指向头节点，形成循环） tail = tail->next;（尾指针向后移动，指向新插入的结点）
在所有结点插入完毕后：L->prior = tail（头指针的前驱指针等于尾指针）
- 循环链表
-
数组还是链表？
- 根据他们的优缺点具体情况具体分析进行选择
- 数组的优缺点
+ 查找速度快
+ 随机访问时直接访问下标，方便
- 插入和删除操作需要大量操作，耗时略久
- 内存空间要求高，必须有足够的连续内存空间
- 数组容易开的过大，造成内存浪费
- 数组大小固定，不能动态拓展 - 链表的优缺点
+ 大小没有固定，拓展灵活
+ 插入删除速度快
+ 内存利用率高，不会浪费内存
- 只能遍历查找，效率低
- 销毁比数组略复杂
1.2 学习体会
进入了新学期的学习，第一章的主要内容还是与上学期的数组和链表基本相同，但正是因为相同又恰恰暴露出来一些问题：以前的内容生疏了。数组左移右移从哪里开始，到哪里结束？实际写代码时出现越界的问题不是一次两次。但其实也不是什么大问题，多写几次，多碰几次壁，慢慢改过来就可以了。尤其是对数组进行操作时，什么时候下标要-1？什么时候下标不变？循环条件要不要等号？一步步改，就能记住该怎么写了。
其他特别大的问题基本没有遇到，希望能在接下来的学习中做到更好吧。
同时也发现了C++的stl库的强大之处，vector、list、map、algorithm等一系列库函数，要了解的东西还有很多很多。
Q2.PTA实验作业
2.1 一元多项式的乘法与加法运算
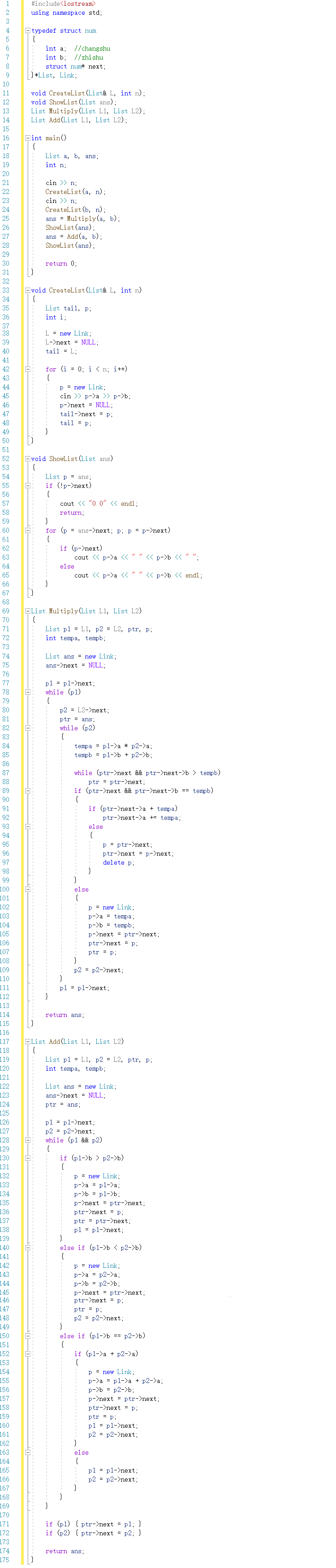
2.1.1 代码截图
2.1.2 PTA提交列表及说明
1.部分正确：对多项式结果应输出0 0的情况判断条件出错，原来判断条件直接写的p，后改为p->next后通过
2.其他问题：在乘法的函数中，我一开始对ptr的循环条件写的是ptr->next->b >= tempb导致我一直跑出错误的结果，在F11和纸上模拟的操作后，终于发现问题将等号去掉
3.其他问题：当乘/加法中出现0的情况时，我一开始的做法是在输出时只输出不为0的内容，但却又引发了一系列奇怪的问题，最终选择直接将系数为0的结点删除
4.个人看法：现在回过头来看这份代码，代码重复的地方太太太多了，阅读起来非常吃力，现在可以考虑用上list库来对代码进行改进了
2.2 两个有序链表序列的交集
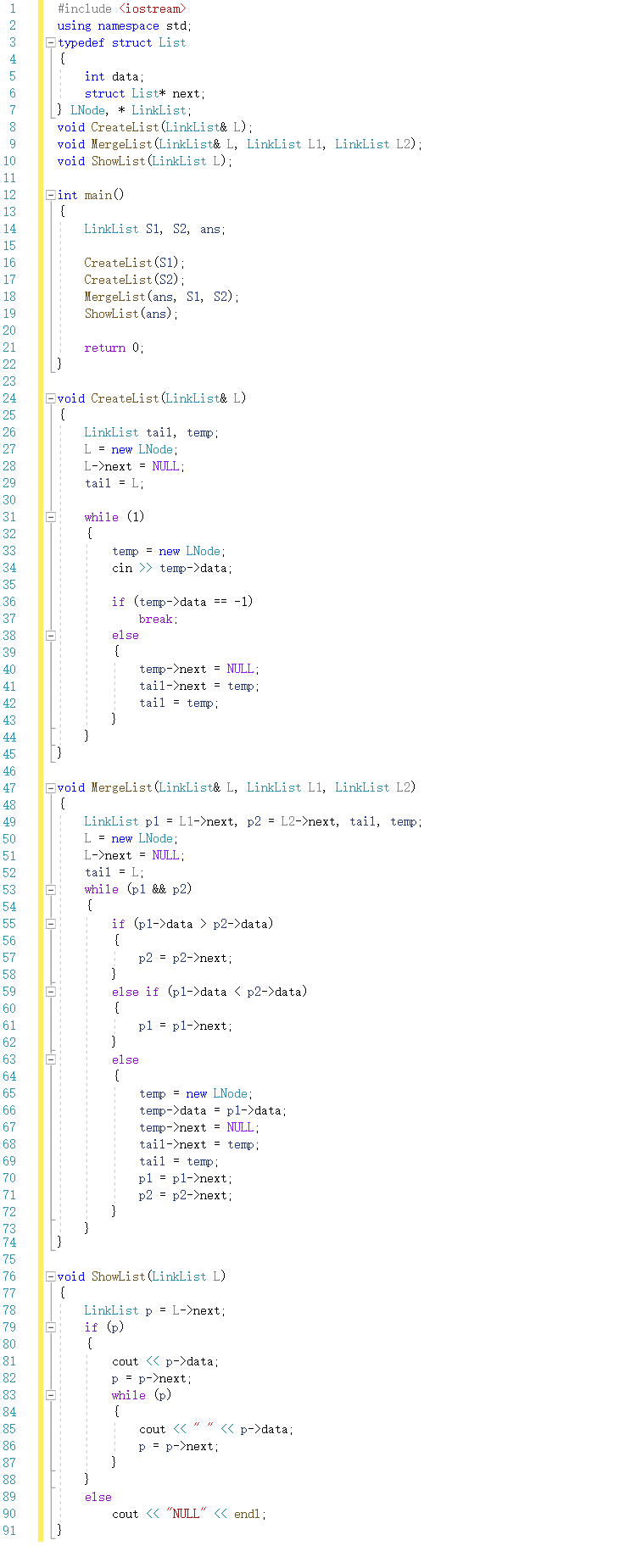
2.2.1 代码截图
2.2.2 PTA提交列表及说明
1.部分正确：没有看完整题目要求，没有按要求输出NULL
2.其他问题：一开始写的时候又犯了老问题，当遇到L1与L2中相等的元素，添加至新链表后，死循环了，因为没有将L1和L2链表继续向下循环
3.个人看法：感觉代码还可以再优化，似乎可以直接在一条链上进行操作？若没有出现相同的元素却出现了比它大的元素，则将该结点删除；若有相同元素则向下遍历，比较下一个元素？
2.3 重排链表
2.3.1 代码截图
2.3.2 PTA提交列表及说明
1.前两个部分正确：这道题真的是多灾多难……一开始我是用循环双链表写的这题，但是多余结点和最大N测试点没有过，多余结点测试点稍加修改通过了，但是最大N测试点依旧超时，毕竟是链表，不断的逐个遍历太耗费时间了，找不到解决方案，只能想用数组来储存数据
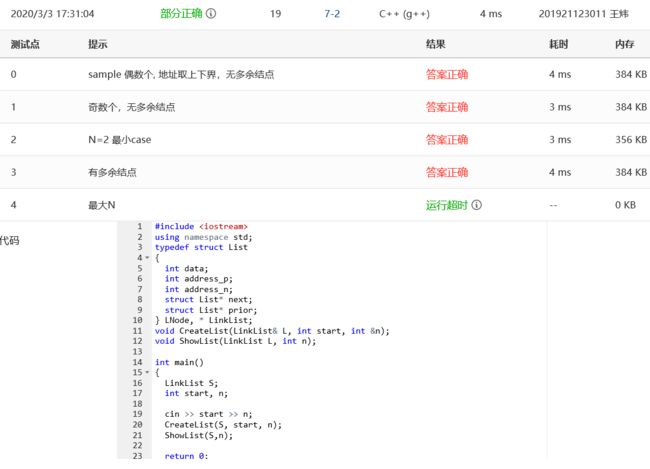
2.中间一大串的0分和1分：于是我选择一开始都使用数组来储存，最后再储存到双链表中（现在想想真是多此一举……早都用数组就好了），结果出现了新问题：内存超限。于是寻求百度：双链表会更占用内存空间吗？但是找不到类似的问题。（至今不懂内存超限错误的原因，我自己VS运行找不到问题……蹲一个解答）
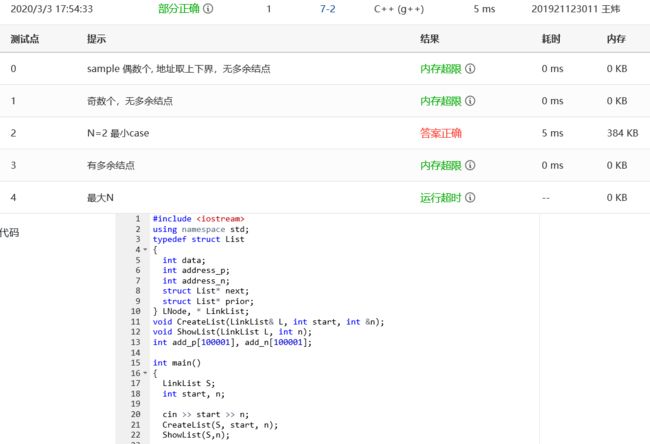
3.答案正确：放弃了双链表，全部使用数组，add1为普通数组，add2为哈希数组，最终经过排序后存到p的结构体数组中，终于通过本题
4.碎碎念：明明题目写的是重排链表，结果最后却用了数组，包括在做完后去网上找其他做法时也全都是数组，佛了
Q3.阅读代码
3.1 复制带随机指针的链表
3.1.1 设计思路
该链表除了一个元素外，还包含一个指向随机结点的指针，所以对于一个节点，除了要处理他前后节点，还要处理它的随机指针
本题要求深拷贝一个链表，除了结点的数据需要复制外还需要保持原来的随机的指针不被破坏。
题解的代码思路如下：
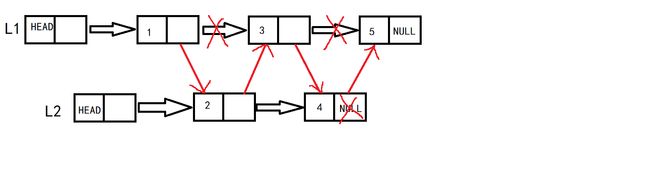
假设有链表
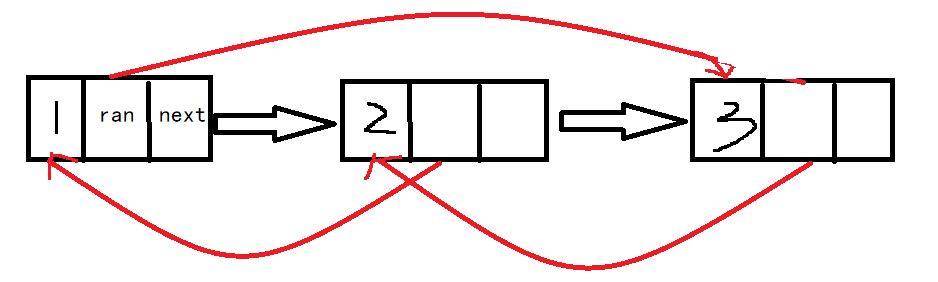
接下来我们将这个链表“复制”
首先应该复制成1[r->3]->1->2[r->1]->2->3[r->2]->3->NULL的状态，其中复制出来的那个结点不包含随机指针
然后跳跃处理，将每个复制出来的结点的随机指针进行复制
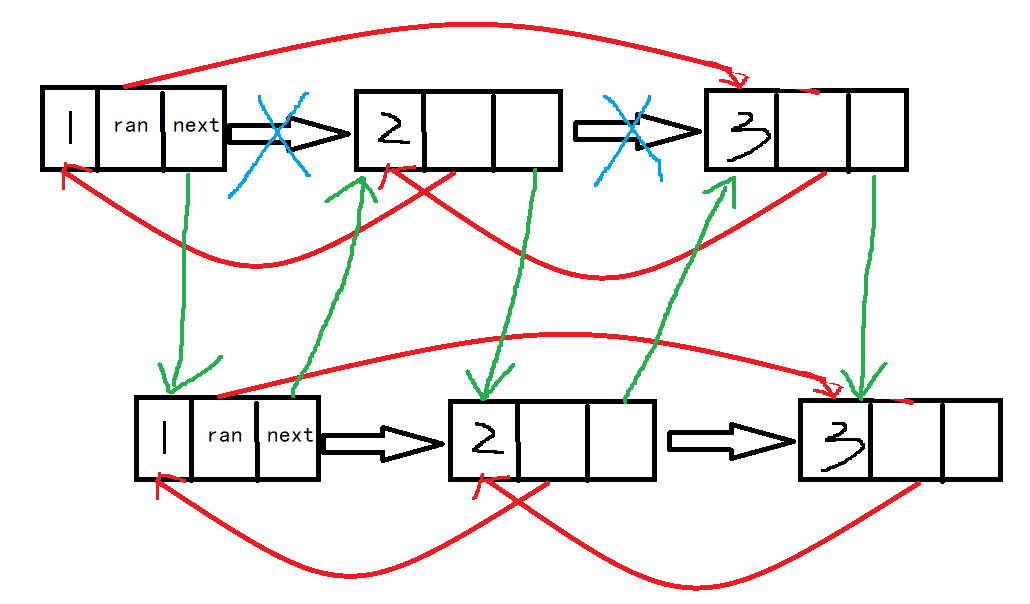
然后将新复制的结点单独拉出来，并恢复原来的链表，即得到两条一摸一样的链表
即为两条1[r->3]->2[r->1]->3[r->2]->NULL的链表，即得到答案
时间复杂度为O(3n)即为O(n)，空间复杂度为O(1)
3.1.2 伪代码
if 头节点为空 then return NULL; end if
初始化遍历指针cur=head
while cur不为空 do
复制当前结点的数据，插入链表中（不包含随机指针）
end while
cur = head;
while cur不为空 do
if cur->random不为空 then
cur->next->random = cur->random->next; //依次给新的节点的随机指针赋值
end if
cur = cur->next->next; //因为复制了一遍，所以要向下遍历两次
end while
cur = head;
初始化指针res=head->next辅助分离链表
while cur不为空 do
分离新旧链表
end while
3.1.3 运行结果
PS：本题是函数题，我没有找到主函数代码，只能自己随便写了一个
3.1.4 分析
- 该题目的难点在于有一个随机指针，随机指针指向链表中的第i个结点或者NULL结点，有可能所有的结点随机指针都指向去NULL或者某个奇怪的结点
- 如果只是按我们以前的想法去做的话，要实现本题会变成以下步骤：先复制原来链表中的数据内容-->再通过原来的链表逐个复制随机结点
- 听起来也不是很复杂对不对？但是如果所有随机结点都指向了尾结点NULL呢？它的时间复杂度可就不是一个级别的了，空间复杂度也变高了
- 而这个题解直接通过“分裂”，直接在原来的链表上复制，以极低的时间和空间复杂度实现最终结果
- 代码简单，思路中最重要的cur->next->random = cur->random->next是点睛之笔，写起来简单但想起来十分困难
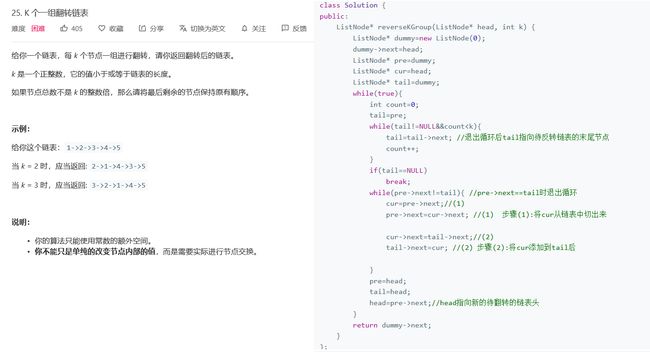
3.2 K个一组反转链表
3.2.1 设计思路
本体要求每K个一组反转链表，例如有链表1->2->3->4->5->6->7，且k为3
那么我们就要每3个结点进行一次反转，最终结果为3->2->1->6->5->4->7
我们以1->2->3->4->5为链表，k=3来看这个题解
题解中使用了3个辅助指针，首先初始化3个指针，prev和tail指针都在头结点，head指针指向prev的next结点
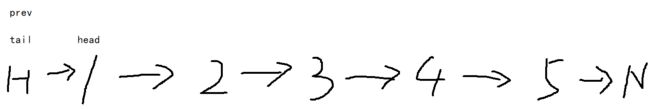
然后让tail指针开始向后移动k次，到达第k个结点
让prev的next结点的元素插入到当前tail结点之后，这样tail结点不断前移，被挪动的元素头插入tail之后的链表
循环这一步，直到prev的next结点即为tail结点
此时第一次翻转完成，让prev、tail结点指向当前head结点，head结点继续指向prev的next结点，完成下一次的初始化，准备第二次翻转
本次tail结点向后移动，遇到了NULL结点，即使也往后走了3个结点，但不进行翻转了
于是就得到最终结果3->2->1->4->5
时间复杂度为O(n)，空间复杂度为O(1)
3.2.2 伪代码
初始化指针，prev与tail指向头结点，head指向头结点的next结点
while 1 do
初始化count为0，用于记录往后走了几个结点
tail=prev
while tail不为NULL且count小于k
tail=tail->next; //这样子能使退出循环后tail结点指向待反转链表的末尾节点
count++;
end while
if tail为NULL then
退出循环，得到结果
end if
while prev的next结点不为tail do
分离出prev的next结点
将prev的next结点插入到tail结点后
end while
pre=head //新一轮的初始化！
tail=head
head=pre->next
end while
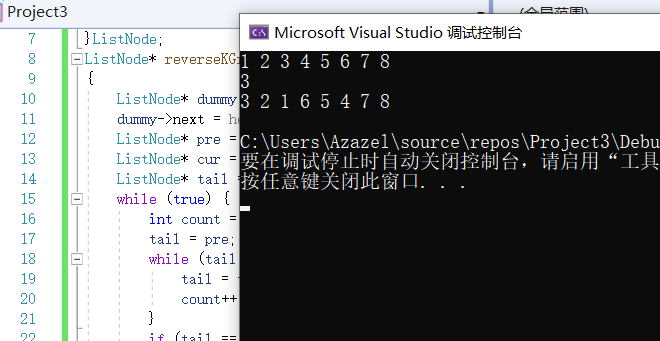
3.2.3 运行截图
3.2.4 分析
- 不同于普通的翻转，本题要求每K个元素将链表的这一部分进行翻转，如何实现不借助其他数据结构的帮助（因为要求你的算法只能使用常数的额外空间）和一小段链表的逆置是本题的难点
- 如果用现有的知识来做这道题，我可能会借助栈来实现本题，每k个元素进栈，然后逐个出栈
- 但是这也意味着更多空间使用，不太符合本题规定
- 这个题解代码最棒的部分我认为是翻转的部分，他让prev的next结点的元素插入到当前tail结点之后，这样做有如下优势：
1.第一次移动让head结点移动，prev下一次该指向的位置即为反转后head结点的位置
2.将新结点头插后tail结点后，使tail指针的位置不断前移，方便判断 - 题解作者通过巧妙地对链表内指针关系进行一定的转换，做到了仅一遍遍历、0额外空间完成题目要求，思路清晰明了，值得学习