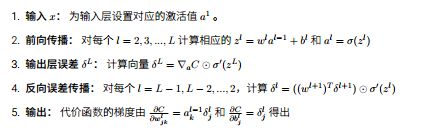SGD方法实现BP神经网络
方法主要参照Nielsen的Neural Networks and Deep Learning
核心规则如下反向算法:(输出层L:惩罚函数C(二次代价函数)对每个节点的敏感度为a(输出层的输出)-y(真实值),即规则3的下三角C;圆圈点为 hadamard乘积)
实现代码(代码附带详细备注):
# encoding: utf-8
"""
@version: python3.5.2
@author: kaenlee @contact: [email protected]
@software: PyCharm Community Edition
@time: 2017/8/9 13:07
purpose:
"""
import numpy as np
from tensorflow.examples.tutorials.mnist import input_data
import random
mnist = input_data.read_data_sets(r'D:\PycharmProjects\HandWritingRecognition\TF\data', one_hot=True)
training_data = list(zip(mnist.train.images, mnist.train.labels))
test_data = list(zip(mnist.test.images, mnist.test.labels))
def Sigmod(z):
return 1 / (1 + np.exp(-z))
def SigmodPrime(z):
"""对S函数求导"""
return Sigmod(z) * (1 - Sigmod(z))
class NetWorks:
# 定义一个神经网络,也就是定义每一层的权重以及偏置
def __init__(self, size):
"""
给出每层的节点数量,包含输出输出层
:param size: list
"""
self.size = size
self.Layers = len(size)
# 以正太分布形式随机赋予初始值
# 每一层的偏置以行保存在list
self.bias = [np.random.randn(num) for num in size[1:]] # 输入层没有bias
# 每层的权重row取决于该层的节点数量,col取决于前面一层的输出即节点数
self.weight = [np.random.randn(row, col) for row, col in zip(size[1:], size[:-1])]
def Feedward(self, a):
"""
d对网络给定输入,输出对应的输出
:param a:@iterable给定的输入向量
:return:
"""
# 上层m节点, 当前n个
# 每一层的输出: W * X.T + b
# W[n, m]
# X: 为上一层(节点数m)的输出[1, m]
# b: [1, n]
a = np.array([i for i in a]) # 输入向量
for b, w in zip(self.bias, self.weight):
z = w.dot(a) + b # 带全输入信号
a = Sigmod(z) # 输出信号
return a
def SGD(self, training_data, epochs, minibatch_size, eta, test_data=None):
"""
随机梯度下降法
:param training_data:输入模型训练数据@[(input, output),...]
:param epochs: 迭代的期数@ int
:param minibatch_size: 每次计算梯度向量的取样数量
:param eta: 学习速率
:param test_data: 训练数据
:return:
"""
if test_data:
n_test = len(test_data)
n = len(training_data)
for e in range(epochs):
# 每个迭代器抽样前先打乱数据的顺序
random.shuffle(training_data)
# 将训练数据分解成多个mini_batch:???,这里讲个样本分批计算了和整体计算区别在哪???
mini_batches = [training_data[k:(k + minibatch_size)] for k in range(0, n, minibatch_size)]
for batch in mini_batches:
# print('bias', self.bias)
self.Update_miniBatchs(batch, eta)
if test_data:
print('Epoch {0}: {1}/{2}'.format(e, self.Evalueate(test_data), n_test))
def Update_miniBatchs(self, mini_batch, eta):
"""
对mini_batch采用梯度下降法,对网络的权重进行更新
:param mini_batch:
:param eta:
:return:
"""
# 用来保存一个计算把周期的权重变换和
B_change = [np.zeros(b.shape) for b in self.bias]
W_change = [np.zeros(w.shape) for w in self.weight]
for x, y in mini_batch:
Cprime_bs, Cprime_ws = self.BackProd(x, y)
B_change = [i + j for i, j in zip(B_change, Cprime_bs)]
W_change = [i + j for i, j in zip(W_change, Cprime_ws)]
# 改变, 原始权重减去改变权重的均值
n = len(mini_batch)
# print('change bias', B_change)
self.bias = [bias - eta/n * change for bias, change in zip(self.bias, B_change)]
self.weight = [weight - eta / n * change for weight, change in zip(self.weight, W_change)]
def BackProd(self, x, y):
"""
反向算法
:param x: iterable,
:param y: iterable
:return:
"""
x = np.array(x)
y = np.array(y)
# 获取没层的加权输入
zs = [] # 每层的加权输入向量, 第一层没有(输入层)
activations = [x] # 每层的输出信号,第一层为x本身
for b, w in zip(self.bias, self.weight):
# print(w.shape)
# print("z", activations[-1])
z = w.dot(activations[-1]) + b
zs.append(z) # 从第二层开始保存带权输入,size-1个
activations.append(Sigmod(z)) # 输出信号a
# print('a', Sigmod(z))
# print(zs)
# print(activations)
# 计算输出层L每个节点的delta
delta_L = self.CostDerivate(activations[-1], y) * SigmodPrime(zs[-1]) # 每个节点输出与y之差 乘 S 在z的偏导数
# 输出成L的c对b偏倒等于delta_L
Cprime_bs = [delta_L]
# c对w的骗到等于前一层的输出信号装置乘当前层的误差
Cprime_ws = [np.array(np.mat(delta_L).T * np.mat(activations[-2]))]
# 计算所有的层的误差
temp = delta_L
# 最后一层向前推
for i in range(1, self.Layers - 1):
# 仅仅需要计算到第二层(且最后一层已知),当前层的delta即b可以用下一层的w、delta表示和当前z表示
# 从倒数第二层开始求解
x1 = (self.weight[-i]).T.dot(temp) # 下一层的权重的装置乘下一层的delta
x2 = SigmodPrime(zs[-i - 1]) # 当前层的带权输入
delta_now = x1 * x2
Cprime_bs.append(delta_now)
Cprime_ws.append(np.array(np.mat(delta_now).T * np.mat(activations[-i-2])))
temp = delta_now
# 改变输出的顺序
Cprime_bs.reverse()
Cprime_ws.reverse()
return (Cprime_bs, Cprime_ws)
def Evalueate(self, test_data):
"""
评估模型
:param test_data:
:return:返回预测正确的数量@int
"""
# 最大数字位置相对应记为正确
res_pred = [np.argmax(self.Feedward(x)) == np.argmax(y) for x, y in test_data]
return sum(res_pred)
def CostDerivate(self, output_acativation, y):
"""
计算最后一个层的误差
:param output_acativation:输出L层的输出信号
:param y: 真实值
:return:
"""
return output_acativation - y
if __name__ == '__main__':
net = NetWorks([784, 20, 10])
# print(net.Feedward([1, 1, 1]))
# print(net.BackProd([1, 1, 1], [1, 0]))
#net.Update_miniBatchs([([1, 1, 1], [1, 0]), ([0, 0, 0], [0, 1])], 0.1)
net.SGD(training_data, 30, 10, 3, test_data)
- 下面为每一迭代期模型识别的准确率(为了计算更加快,这里仅仅用到3层网络,并且隐藏层节点仅为20, 学习步长eta设置在3较理想, 过小学习慢, 过大不易收敛到最优解)
Epoch 0: 9039/10000
Epoch 1: 9182/10000
Epoch 2: 9221/10000
Epoch 3: 9280/10000
Epoch 4: 9316/10000
Epoch 5: 9276/10000
Epoch 6: 9359/10000
Epoch 7: 9334/10000
Epoch 8: 9312/10000
Epoch 9: 9352/10000
Epoch 10: 9333/10000
Epoch 11: 9392/10000
Epoch 12: 9382/10000
Epoch 13: 9395/10000
Epoch 14: 9374/10000
Epoch 15: 9395/10000
Epoch 16: 9361/10000
Epoch 17: 9410/10000
Epoch 18: 9391/10000
Epoch 19: 9403/10000
Epoch 20: 9384/10000
Epoch 21: 9375/10000
Epoch 22: 9386/10000
Epoch 23: 9405/10000
Epoch 24: 9382/10000
Epoch 25: 9398/10000
Epoch 26: 9418/10000
Epoch 27: 9384/10000
Epoch 28: 9404/10000
Epoch 29: 9390/10000