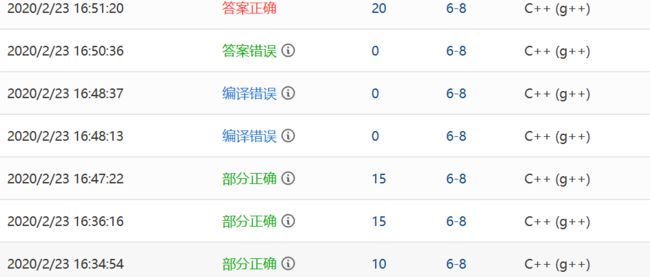
0.PTA得分截图
1.本周学习总结
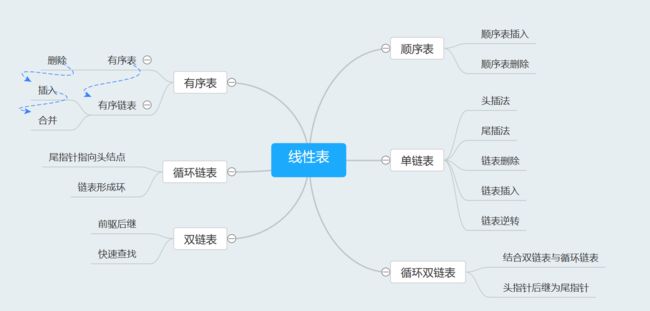
1.1 线性表内容
顺序表结构体定义、顺序表插入、删除的代码操作
定义:把线性表的结点按逻辑次序依次存放在一组地址连续的存储单元里的方法存储的线性表简称为顺序表
顺序表结构体中需要定义两个元素:存放元素的数组以及存放顺序表长度
typedef struct
{
int data[maxsize];//存放元素
int length;//存放顺序表长度
}SqList;
顺序表插入:
原先顺序表:(a1,a2,a3,a4,ai-1,ai....an)
length==n
插入元素e:(a1,a2,a3,a4,ai-1,e,ai...an)
length==n+1
顺序表插入分为表头,表尾,表中,其中插入表尾最方便,只需增长表的长度后插入尾
表头与表中插入均需要挪动表,其中插入表头挪动次数最多
顺序表插入代码
typedef struct{
int data[maxsize];
int length;
}SqList;
void InsertSq(SqList& L, int x)
{
int i = 0;
int j;
for (i = 0; i < L->length; i++)//确定插入位置
{
if (xdata[i])
break;
}
if (i == 0)//当插入表头
{
L->length = L->length + 1;
for (j = L->length; j > 0; j--)
L->data[j] = L->data[j - 1];//将顺序表依次向后挪
L->data[j] = x;
}
else if (i == L->length)//插入表尾
{
L->length = L->length + 1;
L->data[L->length - 1] = x;//将表长增加后,放入表尾
}
else
{
for (j = L->length; j > i; j--)//插入表中
{
L->data[j] = L->data[j - 1];
}
L->data[i] = x;
L->length = L->length + 1;
}
}
顺序表删除
原先顺序表:(a1,a2,a3,a4,ai-1,ai,ai+1...an)
length==n
插入元素e:(a1,a2,a3,a4,ai-1,ai+1...an)
length==n-1
顺序表删除主要在挪动数组,通过元素的覆盖将需要删除的元素剔除
bool Delete(int i,LinkList L,ElemType &e)
{
if(i<1||i>L->length)//判断删除位置是否合法
return false;
else
{
i--;
e=L->data[i];//确定需要删除的元素位于数组的位置
for(int j=i;jlength;j++)//挪动元素
L->data[j] = L->data[j - 1];
L->length--;
}
}
链表结构体定义、头插法、尾插法、链表插入、删除操作
定义:
结构体结指的是一种数据结构,是C语言中聚合数据类型的一类。结构体可以被声明为变量、指针或数组等,用以实现较复杂的数据结构。结构体同时也是一些元素的集合,这些元素称为结构体的成员,且这些成员可以为不同的类型,链表结构体则是通过链表将结构体元素串联在一起
头插法:

头插法,顾名思义就是不断在头结点处插入,因为链表不断增长,而插入只在头结点,所以插入后元素倒序
头插法代码
void CreateListF(LinkList& L, int n)
{
int num;
L = (LinkList)malloc(sizeof(LNode));
LNode* node = NULL;
L->next = NULL;
node = L->next;
for (int i = 0; i < n; i++)
{
node = (LinkList)malloc(sizeof(LNode)); //不断申请结点空间
scanf("%d", &num);
node->data = num;
node->next = L->next;
L->next = node;
}
}
尾插法
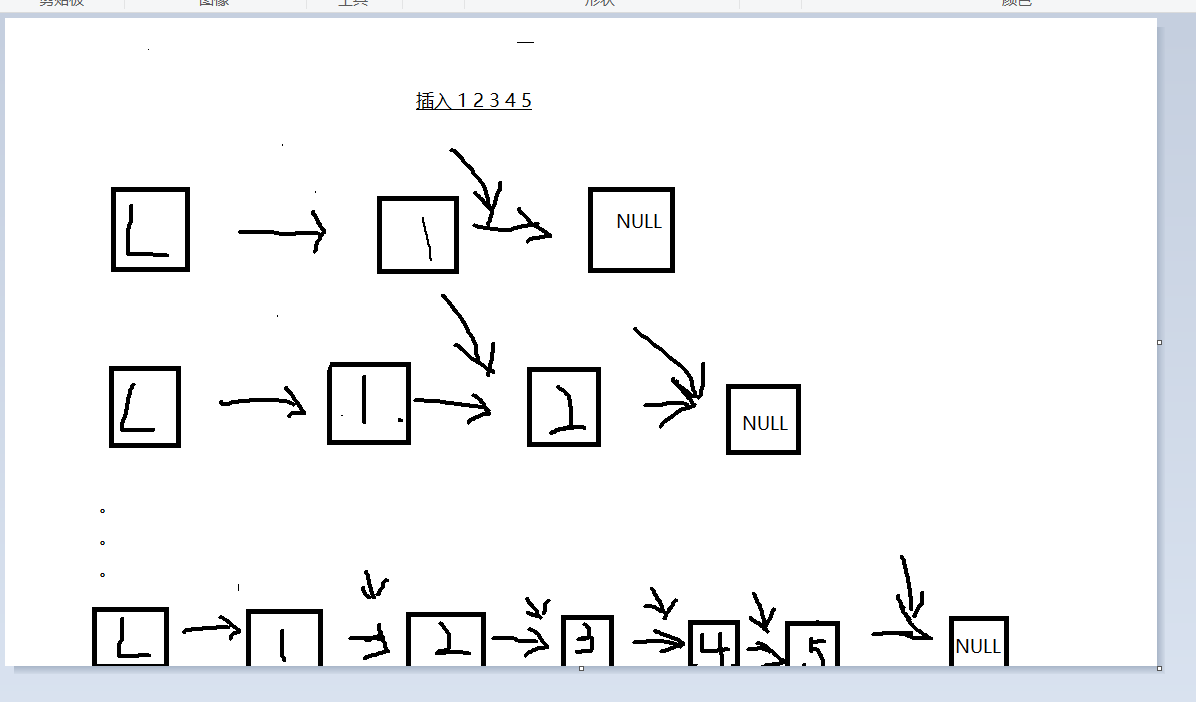
尾插法与头插法不同的是,它需要一个尾指针,通过不断移动尾指针,使它指向插入的元素后,就能按给定顺序插入元素
尾插法代码
void CreateListR(LinkList& L, int n)
{
int num;
LinkList data, r;
L = (LinkList)malloc(sizeof(LNode));
r = L;
for (int i = 0; i < n; i++)
{
data = (LinkList) malloc(sizeof(LNode));
scanf("%d", &num);
data->data = num;
r->next = data;
r = data;
}
r->next = NULL;
}
链表插入元素:第i个元素
1.声明一指针p 指向链表头结点,初始化从1开始;
2.当j 3.若到表末尾p 为空,则说明第i个结点不存在;
4.否则查找成功,在系统中生成一个空结点s;
5.将数据元素e 赋值给s->data;
6.单链表的插入标准语句s->next=p->next; p- >next = s
链表插入元素即改变数据的逻辑结构如:
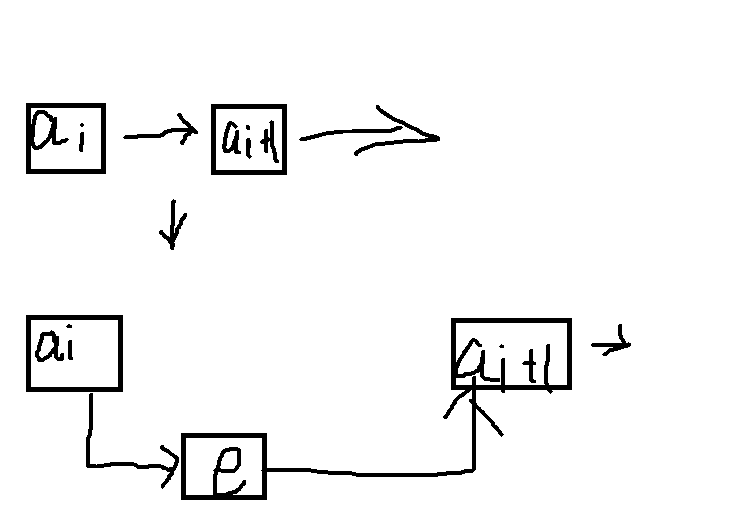
链表插入代码
void ListInsert(LinkList& L, ElemType e,int i)
{
int j=1;
LinkList p,s;
p = L;
while (p&&jnext;
j++;
}
if(j>i||!=p)
return false;
s=new LNode;
s->data=e;
s->next=p->next;
p->next=s;
}
链表删除元素
链表中删除元素,与插入一样,主要在于修改元素指向,不同在于,删除的元素的空间我们要将之释放。
因为涉及链表元素空间释放所以我们不能直接释放,不然会出现程序错误,所以我们需要引入一个中间量
链表删除代码:
void ListDelete(LinkList& L, ElemType e)
{
int flag = 0;
LinkList p = L, s, q;//q为我们需要的中间值
while (p->next)
{
if (p->next->data == e)
{
flag = 1;
q = p->next;
e = q->data;
p->next = q->next;
delete q;
break;
}
p = p->next;
}
if (flag == 0&&L->next!=NULL)
{
printf("%d找不到!\n", e);
}
}
有序表,尤其有序单链表数据插入、删除,有序表合并
有序表定义:表中元素按递增或递减有序排列的线性表
有序顺序表的插入:按照顺序表的排序以递增或递减的顺序插入,保证递增或递减顺序不变
有序表插入代码
void InsertSq(SqList &L,int x)
{
for(int j=L->length;j>0;j--)
{
if(x>=L->data[j-1])
{
L->data[j]=x;
break;
}
L->data[j]=L->data[j-1];
L->data[j-1]=x;
}
L->length++;
}
有序单链表顺序插入:挪动链表去找插入节点的前驱,以方便后续指向关系的修改
void ListInsert(LinkList &L,WlemType e)
{
LinkList pre=L,p;
while(pre->next!=NULL&&pre->next->datanext;//找插入节点的前驱
}
p=new LNode;
p->data=e;
p->next=pre->next;
pre->next=p;
}
有序单链表删除元素
void ListDelete(LinkList& L, ElemType e)
{
int flag = 0;
LinkList p = L, s, q;
while (p->next)
{
if (p->next->data == e)
{
flag = 1;
q = p->next;
e = q->data;
p->next = q->next;
delete q;
break;
}
p = p->next;
}
if (flag == 0&&L->next!=NULL)
{
printf("%d找不到!\n", e);
}
}
有序单链表的插入与删除与链表相同,只是有序单链表中元素具有规律,所以实行操作更方便
有序链表合并
合并在于保持有序,所以需要对两条链进行遍历,并进行每一个节点的比较,以保证插入的有序
所以在合并时遍历链表是一个很重要的过程,在遍历的同时就要进行排序,同时链的长度不一定相同,所以插入完一条后要将另一条剩余的节点放在最后
void MergeList(LinkList& L1, LinkList L2)
{
LinkList newHead = new LNode;
LinkList p = L1;
LinkList q = L2;
LinkList tail = newHead;
while (p && q)
{
if (p->data < q->data)
{
tail->next = p;
p = p->next;
}
else
{
if (p->data == q->data)
{
tail->next = q;
q = q->next;
p = p->next;
}
else
{
tail->next = q;
q = q->next;
}
}
tail = tail->next;
}
if (p) {
tail->next = p;
}
if (q) {
tail->next = q;
}
}
循环链表、双链表结构特点
循环链表:表尾指向的不再是NULL,而是指回表头,将链表形成一个环
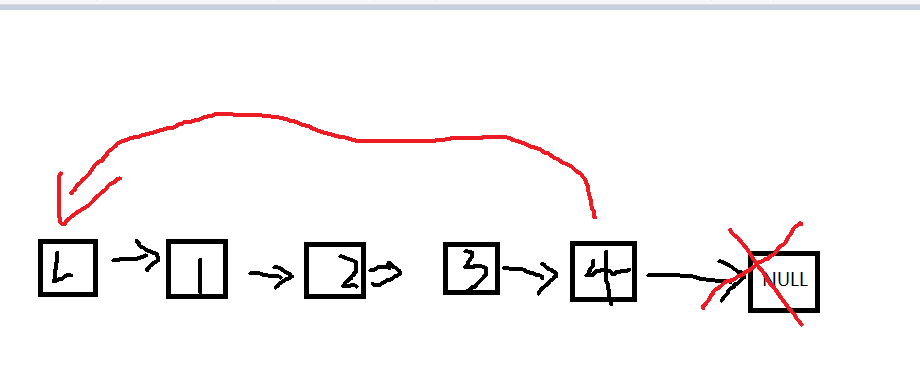
特点:从循环链表的任何一个结点的位置都可以找到其他所有结点且没有明显的尾结点
双链表:它的每个数据结点中都有两个指针,分别指向直接后继和直接前驱。所以,从双向链表中的任意一个结点开始,都可以很方便地访问它的前驱结点和后继结点
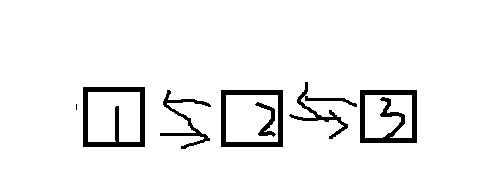
特点:从任意一个结点开始,都可以很方便地访问它的前驱结点和后继结点,从任意结点出发可以访问其他结点
循环双链表
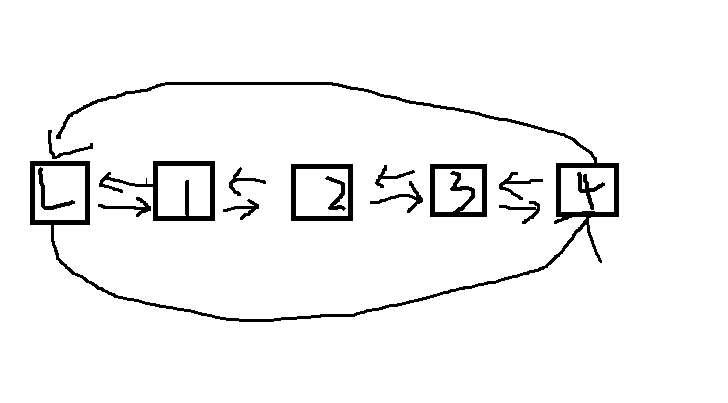
特点:链表中没有空指针域;p所指结点为尾结点的条件为p-next==L;一步操作即L->prior,可以找到尾结点
循环双链表是循环链表与双链表的结合,它查找结点非常方便,且尾结点有了明确
1.2.谈谈你对线性表的认识及学习体会。
对于线性表学习,插入,删除是最常接触的,于是就涉及到时间复杂度,在进行操作时,部分方法虽可行,但是时间复杂度太大,遇到大规模数据就会出现运行超时问题,所以这部分内容,方法是一个很重要的问题,时间复杂度越低的代码越高效。
同时在对链表进行操作,常常会不注意访问就越界了,并且有时链表结点也会出错,所以学习这一部分,一定要动手去试,链表的操作一定要谨慎,关系的修改一定要符合逻辑
2.PTA实验作业(0-2分)
2.1.题目1:6-8 jmu-ds-链表倒数第m个数
2.1.1代码截图(注意,截图,截图,截图。不要粘贴博客上。)
2.1.2本题PTA提交列表说明。
部分正确:三个判断中我只通过了第一个条件,即我一开始只考虑了中间的数,而m为0或者负(即不存在)以及大于链表长度的情况没有考虑
编译错误:条件判断中,将m0写成了m=0,使条件i-m出现错误,同时m被赋值为0,使程序出错
答案错误:我将i-m条件单独放出来,程序可以运行,但是m0还是没有修改所以答案错误
2.2 题目26-11 jmu-ds-链表分割
2.2.1代码截图
2.2.2本题PTA提交列表说明。
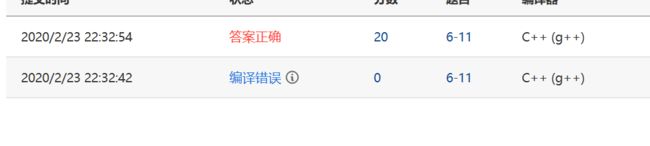
本题主要都是在vs上运行,所以提交并不多
在编写时我曾尝试使用奇数偶数的顺序方法来放各个数据,但是因为我的方法太过复杂以致于后续程序编写难以进行
PTA上提交的方法是通过两个指针来交替分割链表,也可以理解为快慢指针的一种
调试中出现错误有:访问越界,分割错误
访问越界主要是对指针访问没有注意,分割失败是关系之间出现问题
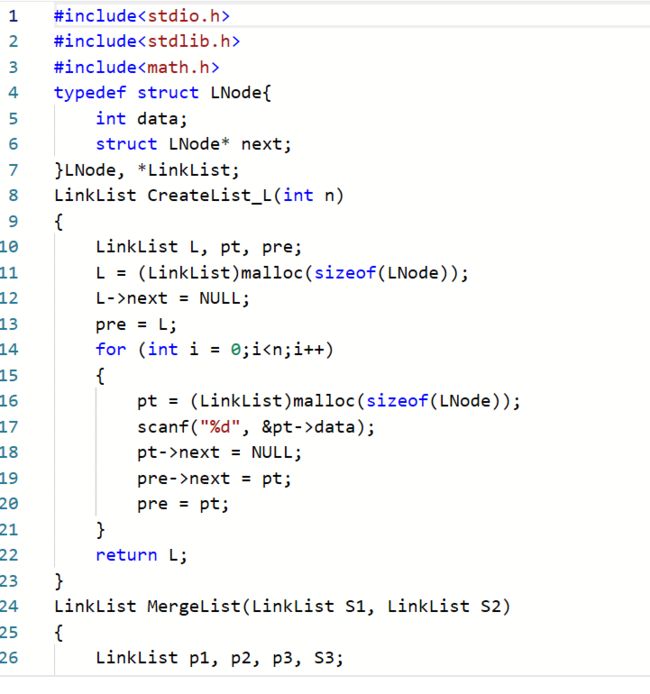
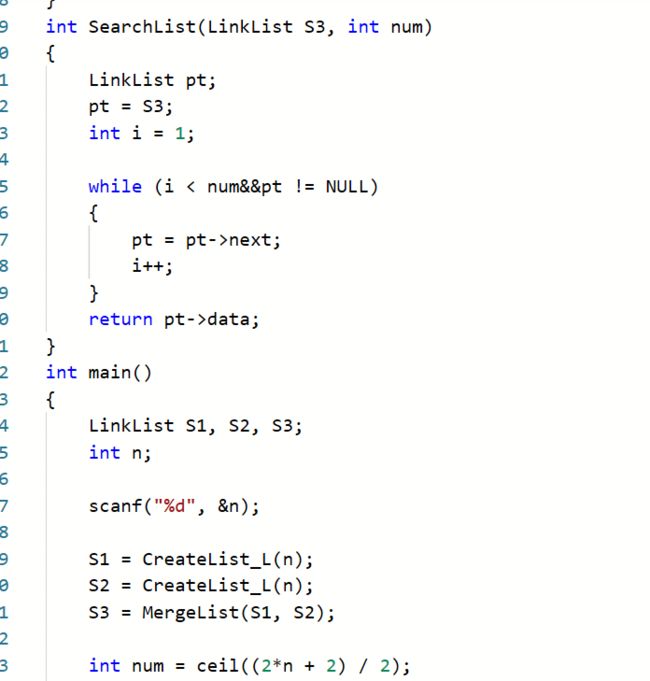
2.3 题目3 7-1 两个有序序列的中位数
2.3.1 代码截图
2.3.2本题PTA提交列表说明。
- 本题在vs运行
最初的方法中,因为无论如何第一个节点比较都会进入相等条件,且不知道到底什么原因所以换了其他方法
vs运行问题:合并两个链表时,因为觉得相等时应该同时移动,所以造成合并出现错误;解决:相等依然只移动一个以保证相等数全部放入
查找中位数时,因为觉得既然是两条一样长度的链所以只需要取第n个数就好,但是奇数长度会出现错误,所以才引入了ceil函数,并对奇偶进行合并讨论
3.阅读代码(0--4分)
找2份优秀代码,理解代码功能,并讲出你所选代码优点及可以学习地方。主要找以下类型代码:
考研题种关于线性表内容。可以找参加过考研的学长学姐拿。尤其是想要考研同学,可以结合本章内容,用考研题训练学习。
ACM题解
leecode面试刷题网站,找线性表相关题目阅读分析。
leecode经典题目
注意:不能选教师布置在PTA的题目。完成内容如下。
3.1 回文链表
if (head == 0 || head->next == 0) return 1;
struct ListNode* slow_p = head, * p = head;
while (p->next != 0 && p->next->next != 0) {
slow_p = slow_p->next;
p = p->next->next;
}
struct ListNode* head_ = slow_p->next;
slow_p->next = 0;
p = head_;
while (p->next != 0) {
slow_p = head_;
head_ = p->next;
p->next = p->next->next;
head_->next = slow_p;
}
while (head_ != 0) {
if (head->val != head_->val) return 0;
head = head->next;
head_ = head_->next;
}
return 1;
3.1.1 该题的设计思路
通过将链表从中间进行分割后反转一个链表,比较链表的每一个节点的值
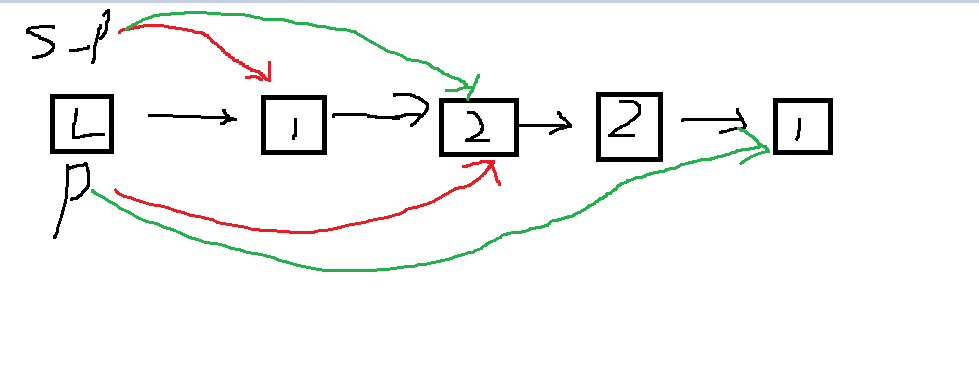
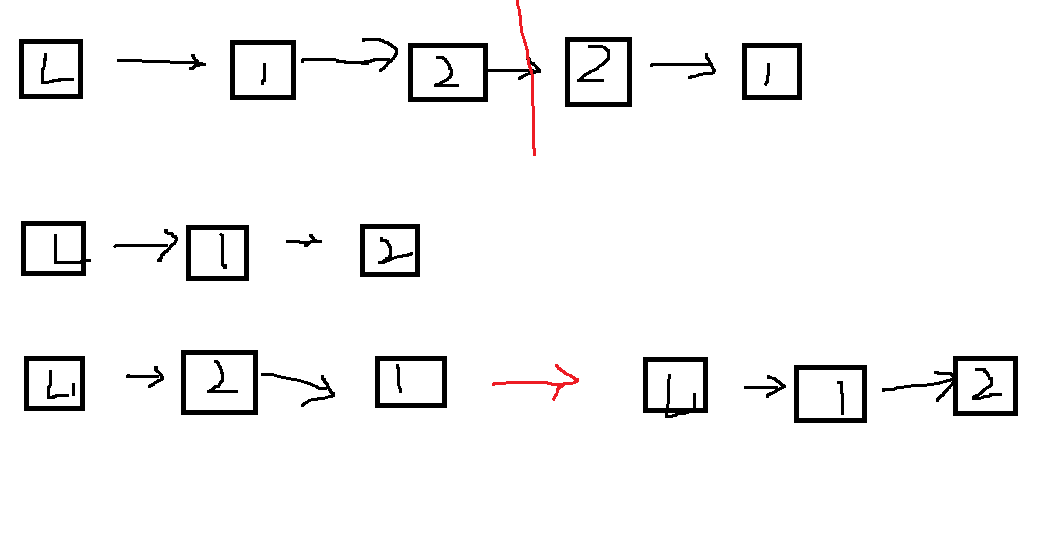
该算法先是找中间结点时遍历一次链表,之后链表一分为二时对分开的链表两次遍历,故时间复杂度为
T(n)=O(n)=n+n/2+n/2=n
空间复杂度为O(1)
3.1.2 该题的伪代码
if (head == 0 || head->next == 0) return 1;//如果链表为空
struct ListNode* slow_p = head, * p = head;
while (p->next != 0 && p->next->next != 0) {//找到链表的中间节点以方便反转链表
slow_p = slow_p->next;
p = p->next->next;
}
//将链表分成两半。
struct ListNode* head_ = slow_p->next;
slow_p->next = 0;
//将第二个链表反转。
p = head_;
while (p->next != 0) {
slow_p = head_;
head_ = p->next;
p->next = p->next->next;
head_->next = slow_p;
}
end while
//按顺序比较两链表val值。
while (head_ != 0) {
if (head->val != head_->val) return 0;
head = head->next;
head_ = head_->next;
}
end while
如果while执行完则为回文
return 1;
3.1.3 运行结果
3.1.4分析该题目解题优势及难点。
回文链表的判断主要在于对链表的遍历,再进行判断,但是如果遇见大规模数据则运行会慢一些,所以该题主要在于如何节省时间
反转链表再用两个指针同时判断,有一个不符马上结束,节省时间,同时该题解不用考虑奇数长度,偶数长度,更方便
3.2 环形链表
class Solution {
public:
bool hasCycle(ListNode* head)
{
ListNode* faster{ head };
ListNode* slower{ head };
if (head == NULL)
return false;
while (faster != NULL && faster->next != NULL)
{
faster = faster->next->next;
slower = slower->next;
if (faster == slower)
return true;
return false;
}
};
3.2.1该题的设计思路
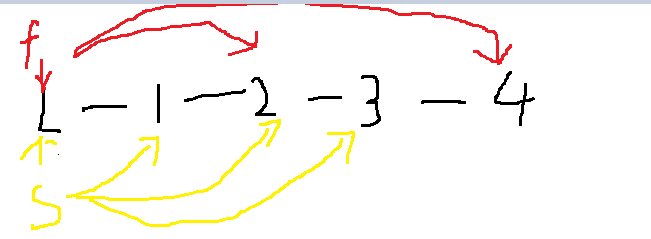
定义快慢指针,来对链表进行遍历,如图,若链表不存在环,则快慢指针不可能碰到,而若存在环,快慢指针不停的跑就一定能遇上
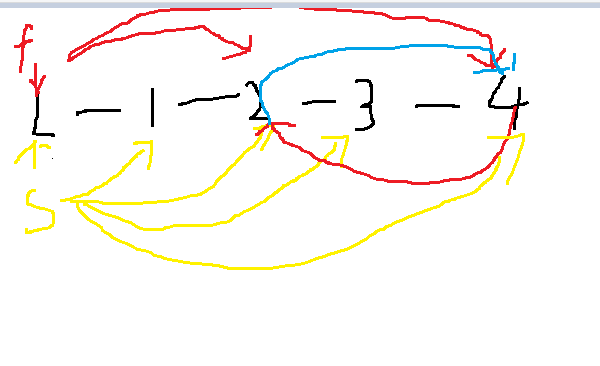
因为从始至终只遍历一次链表所以时间复杂度为
O(n)=n
空间复杂度:O(1)
3.3.2该题的伪代码
两个指针位于同起点head
ListNode* faster{ head }; //快指针
ListNode* slower{ head }; //慢指针
if (head == NULL) //输入链表为空,必然不是循环链表
return false;
while (faster != NULL && faster->next != NULL)
{
faster = faster->next->next; //快指针每次移两步
slower = slower->next; //慢指针每次移一步
if (faster == slower) //他们相遇了
return true; //可以断定是环形链表
}
end while
return false; //快的到终点了,那就不是环形
}
};
3.2.3运行结果
3.2.4分析该题目解题优势及难点
优势:快慢指针的使用能很方便的就得到结果,且整个过程不会很复杂,在时间复杂度上较小
难点:难点在于对快慢指针的应用,让他们同时进行
总的来说,我认为这个题解是很好的