02 主题模型 - SVD矩阵分解、LSA模型

01 主题模型 - 大纲

主题模型 克服了传统信息检索中文档相似度计算方法的缺点，并且能够在海量的数据中找出文字间的语义主题。主题模型在自然语言和给予文本的搜索上起到了重要的作用。

怎样才能生成主题？对文章的主题应该怎么分析？这是主题模型要解决的问题。

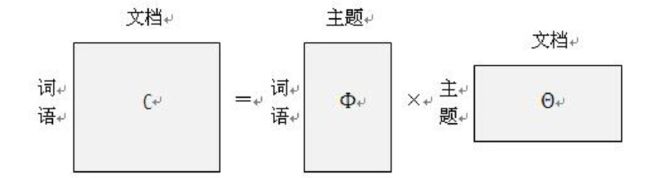
从结果上来看，我们希望将一个包含(词语×文档)的矩阵，分解成(词语×主题)和(主题×文档)两个矩阵相乘的结果。如果可以分解成功，那么矩阵对应的主题向量就是我们所有获取的主题信息。 从而达到了文档分类的结果。

当我们想要提取文档隐含主题的时候，我们可以通过矩阵分解来提取我们需要的信息。下面介绍矩阵分解的算法。

三、SVD 奇异值分解

将m×n的矩阵，分解成三个m×r、r×r、r×n的矩阵。这是我们本质上想要做的事情。但是有些时候我们的原始m×n矩阵比较大，我们可以这样操作：
1、在m×r矩阵中取前k列。
2、在r×r矩阵中我们取对角线的k个元素。
3、在r×n矩阵中取前k行。
即分解形成：m×k、k×k、k×n三个矩阵。这三个矩阵相乘的结果近似于原始矩阵m×n矩阵。

求解SVD的方法：

定义： 现在有矩阵A_n×n，X_n×1是一个向量。如果AX=λX;那么λ就是矩阵A的一个特征值，X是当前特征值λ对应的特征向量。

一个特征向量可以对应多少特征值？1个。
一个特征值可以对应多少特征向量？多个。
为了使特征向量唯一，我们要对特征向量做标准化。
有了特征向量和特征值以后，我们便可以对原始矩阵A进行矩阵分解了。

思考： 我们想将方阵A_n×n分解成：A=WΣW^-1 。
W是特征向量形成的矩阵，Σ是系数，就类似特征值λ；
标准化操作，令 |W|=1 即 W_i^TW_i
∴ W^TW=1 → W^T = W^-1→ A=WΣW^-1
但上述的前提是矩阵A是一个方阵。如果A不是方阵，那么矩阵分解就必须用到SVD的方法。

奇异值分解的几何意义：https://www.jianshu.com/p/e1b8a315fd36

SVD的特性

对于奇异值,它跟我们特征分解中的特征值类似，在奇异值矩阵中也是按照从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。也就是说，我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。

由于可以使用小矩阵来近似的描述样本信息的这个重要特性，SVD可以常用于PCA降维、推荐系统以及主题模型等场景中。

四、LSA模型

潜在语义分析(Latent Semantic Analysis, LSA)，也叫做Latent Semantic Indexing, LSI. 是一种常用的简单的主题模型。LSA是基于奇异值分解(SVD)的方法得到文本主题的一种方式。

分析为什么用近似值： 我们在做奇异值分解的时候，我们可以得到一个矩阵相乘的分解结果。我们认为可以用前K个特征构成一个近似的分解结果。我们来分析一下，如果分解的结果是这样的形式：U_m×m∑_m×nV^T_n×n;分解出来的矩阵大小和我的文章个数 |μ文| 或词的个数 |μ词| 挂钩。如果文章里的词特别多，那么我分解出来的结果，即提取出来的主题个数，不是m就是n，就没有了分解的意义。
所以我们要通过一个近似的方法，k代表的是我们主题的个数。|μ主题|

总结： 我们输入的有m个文本，每个文本有n个词。而Aij则对应第i个文本的第j个词的特征值。k是我们假设的主题数，一般要比文本数少。

SVD分解后：
U_il 对应第i个文本和第l个主题的相关度。
V_jm 对应第j个词和第m个词义的相关度。
Σ_lm 对应第l个主题和第m个词义的相关度

值得注意的是：V_jm词义相关度也是一个隐含变量。
思考： 我们通过奇异值分解出来的是3个矩阵。A_m×n = U_m×k∑_k×kV^T_n×k; 那么三个矩阵需要由几个不同的变量？

1、一个矩阵分解成两个个矩阵的时候，有文章、词语、主题三个变量。我认为多出来的一维变量是主题。

2→3

2、那么现在两个个矩阵矩阵分解到三个矩阵的时候，有文章、词语、主题、词义四个变量。多出来的一维变量是词义。

U_il 对应第i个文本和第l个主题的相关度。
V_jm 对应第j个词和第m个词义的相关度。
Σ_lm 对应第l个主题和第m个词义的相关度

下面通过一个例子来进一步解释这个问题。

LSA案例

假设有10个词、3个文本对应的词频TF矩阵如下：

我们该如何去做矩阵分解？

假定主题数为2，通过SVD降维后的三个矩阵分布为：

通过SVD矩阵分解我们可以得到文本、词与主题、语义之间的相关性，但是这个时候计算出来的内容存在负数，我们比较难解释，所以我们可以对LSI得到文本主题矩阵使用余弦相似度计算文本的相似度的计算。最终我们得到第一个和第三个文档比较相似，和第二个文档不太相似。(备注：这个时候直接在文本主题矩阵的基础上直接应用聚类算法即可)

03 主题模型 - LSA案例

LSA主题模型总结

除非数据规模比较小，而且希望快速的粗粒度的找出一些主题分布关系，否则我们一般不会使用LSA主题模型。

优点：
原理简单，一次SVD分解即可得到主题模型，可以同时解决词义的问题。

缺点：
1、SVD分解的计算非常耗时，对于高维度矩阵做SVD分解非常困难；
2、主题模型数量的选取对于结果的影响非常大，很难选择合适的k值；
3、LSA模型不是概率模型，缺乏统计基础，结果难以直观的解释。

04 主题模型 - NMF
06 主题模型 - pLSA又称pLSI - 基于概率的潜在语义分析模型