Prolog学习:基本概念
上一篇对Prolog有了一个感性的认识,今天介绍下Prolog中一些基本概念,想要用Prolog解决一些实际问题之前必须要先了解它们。这些概念在《七周七语言》这本书中都有介绍,我简单提炼汇总下,就当给这门小众语言做个宣传吧。
变量/规则/知识库
在Prolog中变量的命名是有特殊要求的,如果一个词以小写字母开头,它就是一个原子(atom),类似于其他语言中的符号(symbol),如果一个词以大写或下划线开头,那么它就是一个变量,和其他语言一样变量值可以改变,可以赋值(不过更灵活)。
符号组成一些事实:
likes(zhangsan,lisi).
likes(wangwu,lisi).
likes(chenliu,maqi).
符号和变量在一起可以用来定义规则:
friend(X,Y):- \+(X = Y),likes(X,Z),likes(Y,Z).
事实是我们对这个世界直接观察的结果。规则是关于现实世界的逻辑推论。
事实 + 规则 = 知识库。
上面的规则可以叫做friend/2因为它有两个参数(类似C#方法中的形参),:-读作“如果”,“如果”后面是由一系列“子目标”组成,子目标之间可以是且的关系,用“,”分割,也可以是或者的关系,用“.”表示。Prolog就是通过验证规则来回到我们yes或no的,如果参数能满足所有子目标就是yes。

合一(unification)
合一是Prolog中一个非常重要的概念。简单的来说合一就相当于其它语言中的赋值:
cat(lion). cat(tiger). dorothy(X,Y,Z) :- X = lion,Y = tiger,Z = bear. twin_cast(X,Y) :- cat(X),cat(Y).
合一的意思是:找出那些使规则匹配的值。
所以执行dorothy(lion,tiger,bear).这句,Prolog会返回yes:
dorothy/3规则的右侧,Prolog将lion赋值给X,tiger赋值给Y,bear赋值给Z,就像在命令式语言中这样:
var X = lion; var Y = tiger; var Z = bear;
这些值和左侧(也就是dorothy(lion,tiger,bear))对应的值相匹配,所以合一成功。
不过真正让合一发挥作用的是因为它在规则的两侧都能工作,在GNU Prolog中执行下面的语句:
dorothy(One,Two,Three).
会得到这样的结果:
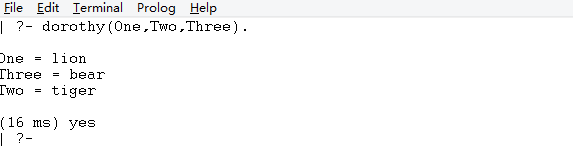
在规则右侧Prolog还是分别将X,Y,Z和lion,tiger,bear进行绑定,而在规则的右侧,Prolog是的One,Two,Three分别和X,Y,Z进行合一了:
One = X = lion; Two = Y = tiger; Three = Z = bear;
并且合一的情况有时候不是唯一的,我们如下执行上面的twin_cast规则:
twin_cast(One,Two).
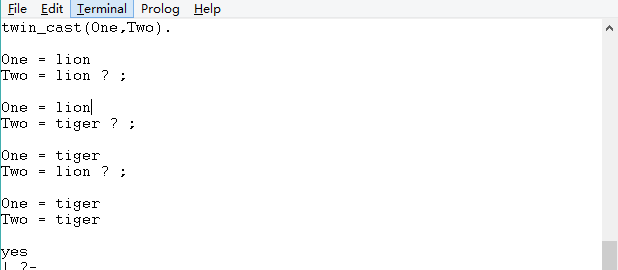
可以通过“;”来进行追问,有时候我们可能不满足于一个答案。
怎么样你是不是已经预见到合一在Prolog中发挥的至关重要的作用了:输出。
列表/元组
只要是语言都会有数据结构,因为程序 = 算法 + 数据结构。
Prolog中有两个非常重要的数据结构:列表和元祖。列表是变长的容器:像[1,2,3]这样表示,元组是定长的容器,像(1,2,3)这样表示。两个数据结构非常简单,但是和合一配合起来的时候会十分强大。
| ?- (1,2,3) = (1,2,3). yes
| ?- [A,B,C] = [A,B,C].
yes
如果两个元组拥有的元素数量相同并且每个元素可以合一 ,则它们整体就是合一的。
加入变量会更有趣:
| ?- [A,B,C] = [1,2,3]. A = 1 B = 2 C = 3 yes
并且变量在哪一侧无所谓,只要Prolog认为它们可以相同,那么就可以合一:
| ?- [A,2,C] = [1,B,3]. A = 1 B = 2 C = 3 (16 ms) yes
这让我想到小时候玩的一种扑克牌游戏了,当抓到大王或小王的时候,我可以把它看做是任何一张牌。
另外列表拥有一个元组不拥有的功能,这个功能在后面介绍的递归中会被广泛使用。 那就是通过[Head|Tail]解析列表,很简单看个例子就明白了:
| ?- [Head|Tail] = [1,2,3,4]. Head = 1 Tail = [2,3,4] yes
Head绑定到1,Tail绑定到剩下的元素,Tail仍然是一个列表。因为Prolog的变量是没有数据类型之分的,所以它可以很容易的绑定为列表或元组,这点有点动态语言的性质,Prolog中也有匿名变量:
| ?- [a,b,c,d,e]=[_,_|[Head|_]]. Head = c yes
这样我们就能指定提取列表中某一个元素了。
递归
我们趁热打铁看看Prolog中递归是怎么发挥作用的,留心它和命令式语言中的不同。
我们就以经典的斐波那契数列做例子吧,我们先来看下命令式语言是如何实现,这个再熟悉不过了:
static void Main(string[] args) { Console.WriteLine(Fibonacci(8)); Console.ReadKey(); }
static int Fibonacci(int n)
{ if (n == 1) return 0; if (n == 2) return 1; return Fibonacci(n - 2) + Fibonacci(n - 1); }
在看Prolog是如何实现之前,我们先来描述一下关于斐波那契数列的既定事实和规则,因为Prolog正是基于事实和规则的一门语言:
- 第一个数是0;
- 第二个数是1;
- 从第三个数开始等它前面两个数之和。
好了和上面对应的Prolog的代码也是三行:
fibonacci(1,0). fibonacci(2,1). fibonacci(N,V) :- N > 2, N1 is N -1, N2 is N -2, fibonacci(N1,V1),fibonacci(N2,V2), V is V1 + V2.
注:is是Prolog中内置的一个谓词。

比较起来你可能觉得和C#代码差不多,都很简洁,Prolog有什么特别的或者说优势呢?其中区别各位自己体会吧,我也在慢慢体会,这个区别就是声明式语言和命令式语言之间的区别。
这个例子太简单不能很好体现Prolog的优势,下一篇文章我们看下用Prolog是如何解决数独和八皇后问题的。我们来看下《七周七语言》这本书中几个递归的例子,也许你能感兴趣不妨试试:
count(0,[]). count(Count,[Head|Tail]):- count(TailCount,Tail),Count is TailCount + 1. sum(0,[]). sum(Total,[Head|Tail]):- sum(Sum,Tail),Total is Sum + Head. average(Average,List):- sum(Sum,List),count(Count,List),Average is Sum/Count.
count是求列表元素的个数,sum是求和,average是求平均值。
内置谓词
所谓内置的谓词,可以简单理解为Prolog提供的一些基本“功能”,就像.net中的一些类库一样。上面提到的is就是。
length:获取列表的长度:
| ?- length([1,2,3],L). L = 3 yes
append:可以用来合并两个列表,当然还有很多其他功能:
| ?- append([1],[2],What). What = [1,2] yes
用于列表的减法:
| ?- append([1],What,[1,2,3]). What = [2,3] yes
排列组合:
| ?- append(One,Two,[1,2,3,4]). One = [] Two = [1,2,3,4] ? ; One = [1] Two = [2,3,4] ? ; One = [1,2] Two = [3,4] ? ; One = [1,2,3] Two = [4] ? ; One = [1,2,3,4] Two = [] (15 ms) yes
fd_domain:验证值是否在一个范围之内:
| ?- fd_domain(1,1,4). yes | ?- fd_domain([1,2,3,4],1,4). yes | ?- fd_domain([1,2,3,5],1,4). no
fd_all_different:检查列表中是否有重复元素:
| ?- fd_all_different([1,2,3]). yes | ?- fd_all_different([1,2,1]). no
member:检查某一个值是否在一个列表内:
| ?- member(1,[1,2]). true ? yes | ?- member(3,[1,2]). no
好了关于Prolog的基本概念就介绍到这,下一篇文章我们会看下通过这些基本概念Prolog是如何解决一些复杂问题的。想了解更多推荐大家去看看这本书。