【杨氏矩阵+勾长公式】POJ 2279 Mr. Young's Picture Permutations

Description

Mr. Young wishes to take a picture of his class. The students will stand in rows with each row no longer than the row behind it and the left ends of the rows aligned. For instance, 12 students could be arranged in rows (from back to front) of 5, 3, 3 and 1 students. 

X X X X X


X X X


X X X


X

In addition, Mr. Young wants the students in each row arranged so that heights decrease from left to right. Also, student heights should decrease from the back to the front. Thinking about it, Mr. Young sees that for the 12-student example, there are at least two ways to arrange the students (with 1 as the tallest etc.): 

 1  2  3  4  5     1  5  8 11 12


 6  7  8           2  6  9


 9 10 11           3  7 10


12                 4

Mr. Young wonders how many different arrangements of the students there might be for a given arrangement of rows. He tries counting by hand starting with rows of 3, 2 and 1 and counts 16 arrangements: 

123 123 124 124 125 125 126 126 134 134 135 135 136 136 145 146


45  46  35  36  34  36  34  35  25  26  24  26  24  25  26  25


6   5   6   5   6   4   5   4   6   5   6   4   5   4   3   3

Mr. Young sees that counting by hand is not going to be very effective for any reasonable number of students so he asks you to help out by writing a computer program to determine the number of different arrangements of students for a given set of rows.

Input

The input for each problem instance will consist of two lines. The first line gives the number of rows, k, as a decimal integer. The second line contains the lengths of the rows from back to front (n1, n2,..., nk) as decimal integers separated by a single space. The problem set ends with a line with a row count of 0. There will never be more than 5 rows and the total number of students, N, (sum of the row lengths) will be at most 30.

Output

The output for each problem instance shall be the number of arrangements of the N students into the given rows so that the heights decrease along each row from left to right and along each column from back to front as a decimal integer. (Assume all heights are distinct.) The result of each problem instance should be on a separate line. The input data will be chosen so that the result will always fit in an unsigned 32 bit integer.

Sample Input

1

30

5

1 1 1 1 1

3

3 2 1

4

5 3 3 1

5

6 5 4 3 2

2

15 15

0

Sample Output

1

1

16

4158

141892608

9694845

题意：给出行数k，以及每行数字的个数n[i]，问一共有多少种排列方法使元素从左到右从上到下依次递减。（即构成一个杨氏矩阵）。
分析：勾长公式。暴力+公式；

杨氏矩阵（杨表）（面试会问到）

杨表由有限的方格组成。

对于一个正整数，给定一个整数分拆λ(10=1+4+5)，则对应一个杨表（注意这是一个递降的过程，也就是说下面一行的方格数要大于等于上一行的方格数）。

 

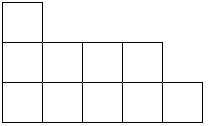
一个（1,4,5）分拆表示的杨表

杨表与整数分拆λ一一对应。

给定一个杨表，一共有n个方格。那么把1到n这n个数字填到这个杨表中，使得每行从左到右都是递增的，每列从下到上也是递增的。如图

 

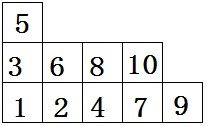
一个杨表的表示

【勾长】对于杨表中的一个方格v，其勾长hook(v)等于同行右边的方格数加上同列上面的方格数，再加上1（也就是他自己）。

【勾长公式】用表示杨表个数，则

 

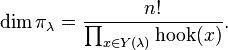
对于分拆10 = 5 + 4 + 1 的应的杨表. 因此共有

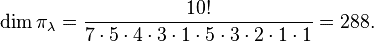种方法。

公式题。求出同行右边的方格数+同列上面的方格数+1。唯一注意的地方是最后除的时候要防止溢出。

 1 LL ans = 1;

 2 for(int i = 1; i <= tot; i++)

 3 {

 4     factor[i] = i;

 5     for(int j = 1; j <= tot; j++)

 6     {

 7         int tmp = gcd(factor[i], young[j]);

 8         factor[i] /= tmp;

 9         young[j] /= tmp;

10     }

11 }

12 //经过上述处理后young[i]均变为1，至于原因，分子除分母是整数，结果分母一定会变为1。

13 for(int i = 1; i <= tot; i++)

14 {

15     ans *= factor[i];

16 }

代码：

 1 /*

 2 Problem: poj_2279

 3 tags: 杨氏矩阵+勾长公式

 4 */

 5 

 6 #include<iostream>

 7 #include<cstdio>

 8 #include<cstdlib>

 9 #include<cstring>

10 #define mems(x, t) memset(x, t, sizeof(x));

11 using namespace std;

12 typedef long long LL;

13 const int maxn = 110;

14 const int INF = 0x3f3f3f3f;

15 

16 int k, tot, n[maxn];

17 int table[maxn][maxn], young[210], factor[210];

18 LL gcd(LL a, LL b)

19 {

20     return b == 0? a : gcd(b, a%b);

21 }

22 int main()

23 {

24     while(~scanf("%d", &k) && k)

25     {

26         mems(table, 0);

27         tot = 0;

28         for(int i = 1; i <= k; i++)

29         {

30             scanf("%d", &n[i]);

31             tot += n[i];

32             for(int j = 1; j <= n[i]; j++)

33             {

34                 table[i][j] = 1;

35             }

36         }

37         mems(young, 0);

38         int cnt = 1;

39         for(int i = 1; i <= k; i++)

40         {

41             for(int j = 1; j <= n[i]; j++)

42             {

43                 if(table[i][j] == 1)

44                 {

45                     young[cnt]++;

46                     for(int l = i+1; l <= k; l++)

47                     {

48                         if(!table[l][j]) break;

49                         young[cnt]++;

50                     }

51                     young[cnt] += n[i]-j;

52                     cnt++;

53                 }

54             }

55         }

56         LL ans = 1;

57         for(int i = 1; i <= tot; i++)

58         {

59             factor[i] = i;

60             for(int j = 1; j <= tot; j++)

61             {

62                 int tmp = gcd(factor[i], young[j]);

63                 factor[i] /= tmp;

64                 young[j] /= tmp;

65             }

66         }

67         for(int i = 1; i <= tot; i++)

68         {

69             ans *= factor[i];

70         }

71         printf("%lld\n", ans);

72     }

73     return 0;

74 }

View Code