【回文串-Manacher】
Manacher算法能够在O(N)的时间复杂度内得到一个字符串以任意位置为中心的回文子串。其算法的基本原理就是利用已知回文串的左半部分来推导右半部分。
转:http://blog.sina.com.cn/s/blog_70811e1a01014esn.html
首先,在字符串s中,用rad[i]表示第i个字符的回文半径,即rad[i]尽可能大,且满足:
s[i-rad[i],i-1]=s[i+1,i+rad[i]]
很明显,求出了所有的rad,就求出了所有的长度为奇数的回文子串.
至于偶数的怎么求,最后再讲.
假设现在求出了rad[1..i-1],现在要求后面的rad值,并且通过前面的操作,得知了当前字符i的rad值至少为j.现在通过试图扩大j来扫描,求出了rad[i].再假设现在有个指针k,从1循环到rad[i],试图通过某些手段来求出[i+1,i+rad[i]]的rad值.
根据定义,黑色的部分是一个回文子串,两段红色的区间全等.
因为之前已经求出了rad[i-k],所以直接用它.有3种情况:
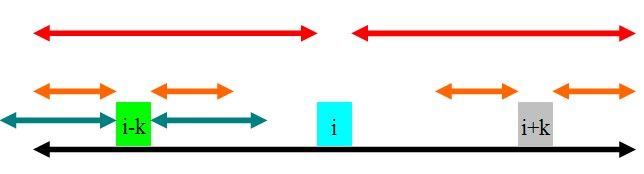
①rad[i]-k<rad[i-k]
如图,rad[i-k]的范围为青色.因为黑色的部分是回文的,且青色的部分超过了黑色的部分,所以rad[i+k]肯定至少为rad[i]-k,即橙色的部分.那橙色以外的部分就不是了吗?这是肯定的.因为如果橙色以外的部分也是回文的,那么根据青色和红色部分的关系,可以证明黑色部分再往外延伸一点也是一个回文子串,这肯定不可能,因此rad[i+k]=rad[i]-k.为了方便下文,这里的rad[i+k]=rad[i]-k=min(rad[i]-k,rad[i-k]).
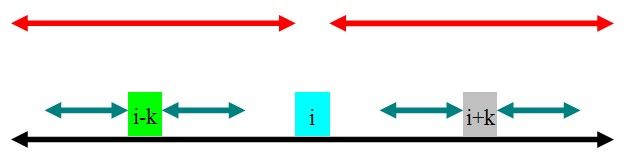
②rad[i]-k>rad[i-k]
如图,rad[i-k]的范围为青色.因为黑色的部分是回文的,且青色的部分在黑色的部分里面,根据定义,很容易得出:rad[i+k]=rad[i-k].为了方便下文,这里的rad[i+k]=rad[i-k]=min(rad[i]-k,rad[i-k]).
根据上面两种情况,可以得出结论:当rad[i]-k!=rad[i-k]的时候,rad[i+k]=min(rad[i]-k,rad[i-k]).
注意:当rad[i]-k==rad[i-k]的时候,就不同了,这是第三种情况:
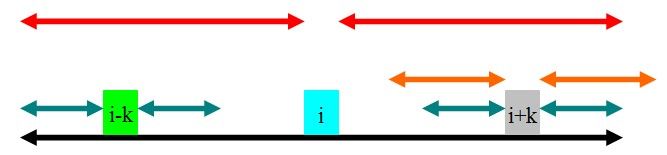
如图,通过和第一种情况对比之后会发现,因为青色的部分没有超出黑色的部分,所以即使橙色的部分全等,也无法像第一种情况一样引出矛盾,因此橙色的部分是有可能全等的,但是,根据已知的信息,我们不知道橙色的部分是多长,因此就把i指针移到i+k的位置,j=rad[i-k](因为它的rad值至少为rad[i-k]),等下次循环的时候再做了.
整个算法就这样.
至于时间复杂度为什么是O(n),我已经证明了,但很难说清楚.所以自己体会吧.
上文还留有一个问题,就是这样只能算出奇数长度的回文子串,偶数的就不行.怎么办呢?有一种直接但比较笨的方法,就是做两遍(因为两个程序是差不多的,只是rad值的意义和一些下标变了而已).但是写两个差不多的程序是很痛苦的,而且容易错.所以一种比较好的方法就是在原来的串中每两个字符之间加入一个特殊字符,再做.如:aabbaca,把它变成(#a#a#b#b#a#c#a#),左右的括号是为了使得算法不至于越界。这样的话,无论原来的回文子串长度是偶数还是奇数,现在都变成奇数了.
HDU-3068 最长回文
分析:直接套上算法即可,注意插入一些字符来使得算法能够适应长度为奇数和偶数的情况。

#include <cstdlib> #include <cstring> #include <cstdio> #include <iostream> #include <algorithm> using namespace std; const int N = 110005; char str[N], cpy[N<<1]; int seq[N<<1]; void manacher(char s[], int length, int rad[]) { for (int i=1,j=0,k; i < length; i+=k) { while (s[i-j-1] == s[i+j+1]) ++j; rad[i] = j; for (k = 1; k <= rad[i] && rad[i-k] != rad[i]-k; ++k) { // 利用类似镜像的方法缩短了时间 rad[i+k] = min(rad[i-k], rad[i]-k); } j = max(j-k, 0); } } int main() { while (scanf("%s", str) != EOF) { int len = strlen(str); cpy[0] = '(', cpy[1] = '#'; for (int i=0, j=2; i < len; ++i, j+=2) { cpy[j] = str[i]; cpy[j+1] = '#'; } len = len*2+3; cpy[len-1] = ')'; manacher(cpy, len, seq); int Max = 1; for (int i = 0; i < len; ++i) { Max = max(Max, seq[i]); } printf("%d\n", Max); } return 0; }
HDU-4513 吉哥系列故事——完美队形II
题意:给定一个数列,长度最长达到100000,要求找出一个最长的左边单调递增,右边单调递减的回文子串。
分析:刚开始的错误想法想法是所有的合法的解必定是一个回文串,因此把以任意一点为中心的所有回文串长度求出来,然后按照长度由长到短排一个序,暴力先判定最长的单调回文串,然后依据当前的最优值进行剪枝,不过还是TLE。网上看了下别人的想法,都说是一个Manacher的应用,而且貌似别人的模板和我的不太一样,现在来说说我的理解。
其实一开始的时候我就有想过直接定义一个单调回文来做,但是仔细想想,如果某个单调回文已经求了出来,那么其左翼对应右翼肯定不会是一个单调回文,因为左翼一定是一个单调的序列,不会出现以一个为中心向两边下降的情况,当然除非出现相同的值。之所以出现这种想法是因为我以为只有左翼里面包含回文子串才会使得时间复杂度降低,而时间上该题的模型中,求出了一个单调回文区间,那么利用左翼的对应面不可能产生单调回文同样能够加速匹配。总而言之,该算法就是通过求回文来使得右翼的值复制左翼的值达到降低时间复杂度的目的,因此该题只要更改扩展原则即可,由单一的相等改为单调递增或递减。

#include <cstdlib> #include <cstring> #include <cstdio> #include <algorithm> #include <iostream> using namespace std; const int N = 100005; const int inf = 0x3f3f3f3f; int n; int seq[N<<1]; int rad[N<<1]; inline bool check(int seq[], int a, int b) { if (seq[a] != seq[b]) return false; if (!seq[a] && !seq[b] || a == b) return true; int ar = a+2, bl = b-2; if (seq[a] <= seq[ar]) return true; return false; } void manacher(int seq[], int rad[], int length) { for (int i=1,j=0,k; i<length; i+=k,j-=k) { while (check(seq, i-j-1, i+j+1)) ++j; rad[i] = j; for (k=1; k<=j && rad[i-k]!=rad[i]-k; ++k) { rad[i+k] = min(rad[i-k], rad[i]-k); } } } inline void getint(int &t) { char ch; while ((ch = getchar()), ch < '0' || ch > '9') ; t = ch - '0'; while ((ch = getchar()), ch >= '0' && ch <= '9') { t = t * 10 + ch - '0'; } } int main() { int T; scanf("%d", &T); while (T--) { memset(seq, 0, sizeof (seq)); scanf("%d", &n); seq[0] = inf-1; for (int i=2,j=0; j < n; i+=2,++j) { getint(seq[i]); } n = n*2+3; seq[n-1] = inf-2; manacher(seq, rad, n); int ret = 1; for (int i = 0; i < n; ++i) { ret = max(ret, rad[i]); } printf("%d\n", ret); } return 0; }
zstu-3769 数回文子串
题意:给定一个字符串序列,统计其中一共有多少个回文串,串的长度大于1。
分析:Manacher算法分析出以每一个位置为中心的长度,相加即可。

#include <cstdlib> #include <cstring> #include <cstdio> #include <iostream> #include <algorithm> using namespace std; const int N = 100005; char seq[N]; char cpy[N<<1]; int rad[N<<1]; void manacher(char str[], int rad[], int len) { for (int i=1,j=0,k; i < len; i+=k,j-=k) { while (str[i-j-1] == str[i+j+1]) ++j; rad[i] = j; for (k=1; k<=j && rad[i-k]!=rad[i]-k; ++k) { rad[i+k] = min(rad[i-k], rad[i]-k); } } } int main() { while (scanf("%s", seq) != EOF) { int len = strlen(seq); cpy[0] = '(', cpy[1] = '#'; for (int i=2,j=0; j < len; i+=2,++j) { cpy[i] = seq[j]; cpy[i+1] = '#'; } len = len*2+3; cpy[len-1] = ')'; manacher(cpy, rad, len); int ret = 0; for (int i = 0; i < len; ++i) { ret += rad[i] / 2; } printf("%d\n", ret); } return 0; }
HDU-3948 The Number of Palindromes
题意:给定一个长度为N的字符串,统计其中一共有多少个不同的回文子串。
分析:本来自己想的方法是manacher处理的同时暴力保留回文串,然后set去重,有算法本身可以知道若一个串是回文串,那么根据左右对称,在第二次循环镜像更新时便可知道右边的回文串在前面就被统计过了,所以不同的回文串只要在第一次扩充之后进行判定即可,因此也可知道不同回文串的个数是O(N)级别的。可惜我的方法还是超时了,遇到极端的aa...aa就会重复构造一个子串。
看到博客好像貌似可以使用后缀数组写,不会后缀数组只有另辟他径了。由于回文串的个数是O(N)级别的,因此可以直接枚举每一个中心点,从长度最长的回文串进行枚举,使用字符串hash(多项式插值取模)来判定是否已经被统计过,如果这个长串已经统计过就可以直接跳过了(因为长串中的短串在之前也一定统计过了)。
关于多项式插值取模:在给定一个字符串左右区间的情况下O(1)计算出其hash值。设一个串为1234123,那么定义一个数组sum[i],其中:
sum[1] = 1, sum[2] = 1*T+2, sum[3] = 1*T^2+2*T+3, sum[4] = 1*T^3+2*T^2+3*T+4 ......
通过这样的定义,[L,R]的值就为sum[R]-sum[L-1]*T^(R-L+1)。

#include <cstdlib> #include <cstring> #include <cstdio> #include <iostream> #include <algorithm> #include <string> #include <cctype> #include <set> using namespace std; typedef unsigned long long uint; const int N = 100005; char seq[N]; char cpy[N<<1]; int rad[N<<1]; const int muts = 37; uint mutpower[N]; uint sum[N]; struct hash_map { const static int mod = N*3+2; int idx, head[mod]; struct hash_tables { uint key; int next; }ele[N*2]; void init() { idx = 0; memset(head, 0xff, sizeof (head)); } void clear() { // clear的效率要高于init的效率,后期的用以替换init for (int i = 0; i < idx; ++i) head[ele[i].key%mod] = -1; idx = 0; } bool find(uint x) { int hashcode = x%mod; for (int i = head[hashcode]; i!=-1; i=ele[i].next) { if (ele[i].key == x) return true; } return false; } void insert(uint x) { int tmp = x % mod; ele[idx].key = x; ele[idx].next = head[tmp]; head[tmp] = idx++; } }; // 将hash表的实现封装成一个类 hash_map hash; void manacher(char str[], int rad[], int len) { for(int i=1,j=0,k; i < len; i+=k, j=max(j-k,0)) { while (str[i-j-1] == str[i+j+1]) ++j; rad[i] = j; for (k=1; k<=j && rad[i-k] != rad[i]-k; ++k) { rad[i+k] = min(rad[i-k], rad[i]-k); } } } // str串以i为中心,回文半径为j的回文串剔除插入字符后的hashcode uint gethashcode(char str[], int i, int j) { int L, R; // 在原来字符串中该回文串左右界 uint ret; if (isalpha(str[i])) { // 如果中心字符为字母 L = i/2-1 - j/2; R = i/2-1 + j/2; } else { L = i/2 - j/2; R = i/2-1 + j/2; } ret = sum[R]; if (L) ret -= sum[L-1]*mutpower[R-L+1]; return ret; } void gao(char str[], int len) { // 枚举每一点作为回文串的中心 int ret = 0; for (int i = 2; i < len-2; ++i) { int ee = (bool)(!isalpha(str[i])); for (int j = rad[i]; j >= ee; j-=2) { uint hashcode = gethashcode(str, i, j); if (!hash.find(hashcode)) { ++ret; hash.insert(hashcode); } else { // 如果一个长串已经在hash表里面,那么短的回文串也一定在里面 break; } } } printf("%d\n", ret); } int main() { mutpower[0] = 1; for (int i = 1; i < N<<1; ++i) { mutpower[i] = mutpower[i-1] * muts; } hash.init(); int T, ca = 0; scanf("%d", &T); while (T--) { scanf("%s", seq); hash.clear(); int len = strlen(seq); sum[0] = seq[0]-'a'+1; // 避免0元素的出现,其将导致00和0无区别 for (int i = 1; i < len; ++i) { // 做出一个前缀的多项式值模式 sum[i] = sum[i-1]*muts+seq[i]-'a'+1; } cpy[0] = '(', cpy[1] = '#'; for (int i=2,j=0; j < len; i+=2,++j) { cpy[i] = seq[j]; cpy[i+1] = '#'; } len = len*2+3; cpy[len-1] = ')'; printf("Case #%d: ", ++ca); manacher(cpy, rad, len); gao(cpy, len); } return 0; }
ZOJ-3661 Palindromic Substring
题意:给定一个字符串,现在取出串中回文串的一半,奇数回文的取左边部分加上中心元素,偶数回文取左边的一半,现在给一个回文串一个权值,要求统计所有回文串权值中倒数第K小的值为多少。
分析:主要想法是通过Manacher算法处理出以每个字符为中心所产生的回文半径的长度,然后将每个回文串的按照长度从长到短倒着插入到字段树中,插入的过程中访问hash表是否已经插入过回文串,hash表直接保存着上次回文串插入的位置,这样就可以O(1)的时间找到要插入的位置,然后将多出来的长度插入即可。由于上题中已经得知回文串的个数最多是O(N)的,因此这里插入字段树的次数也会控制在O(N)以内。最后通过遍历一次字典树得到最终的结果,从某节点出发,其子树上的数量将要累加到父亲节点上,因为这个子节点都包括这个父亲节点所表示的回文串。另外奇数串和偶数串需要分开处理。

#include <cstdlib> #include <cstring> #include <cstdio> #include <vector> #include <iostream> #include <algorithm> using namespace std; typedef unsigned long long LL; const int MOD = 777777777; const int N = 100005; const int P = 37; char seq[N]; char cpy[N<<1]; int rad[N<<1]; int val[30]; LL POW[N]; LL sum[N]; vector<pair<LL, int> >vt; int n, m; void manacher(char str[], int rad[], int len) { for (int i=1,j=0,k; i < len; i+=k,j-=k) { while (str[i-j-1] == str[i+j+1]) ++j; rad[i] = j; for (k=1; k<=j && rad[i-k]!=rad[i]-k; ++k) { rad[i+k] = min(rad[i-k], rad[i]-k); } } } LL getkey(int l, int r) { if (!l) return sum[r]; else return sum[r]-sum[l-1]*POW[r-l+1]; } struct Hash_map { static const int mod = N*3+2; int idx, head[mod]; struct hash_tables { LL key; // 字符串hash之后的值 int pos; // pos表示在字段树中的位置 int nxt; }ele[N]; // 最多N个不同回文串 void init() { idx = 0; memset(head, 0xff, sizeof (head)); } void clear() { for (int i = 0; i < idx; ++i) { head[ele[i].key%mod] = -1; } idx = 0; } int find(LL _key) { int id = _key % mod; for (int i = head[id]; ~i; i=ele[i].nxt) { if (ele[i].key == _key) { // 如果该元素在hash表中,说明已经插入到了字典树当中 return ele[i].pos; } } return -1; // 如果没有搜索到的话,返回-1 } void insert(LL _key, int _pos) { int id = _key % mod; ele[idx].key = _key, ele[idx].pos = _pos; ele[idx].nxt = head[id], head[id] = idx++; } }; Hash_map hash; struct Trie { int root, idx; struct Node { int ch[26]; int end; }ele[N]; // 这个空间会不会小了呢 int malloc() { ele[idx].end = 0; memset(ele[idx].ch, 0xff, sizeof (ele[idx].ch)); return idx++; } void init() { idx = 0; root = malloc(); } void insert(int p, int l, int r, int axis) { for (int i = r; i >= l; --i) { ele[p].ch[seq[i]-'a'] = malloc(); p = ele[p].ch[seq[i]-'a']; hash.insert(getkey(i, axis), p); } ++ele[p].end; } int cal(int p, LL fac, LL value) { int tot = ele[p].end; for (int i = 0; i < 26; ++i) { if (ele[p].ch[i] != -1) { tot += cal(ele[p].ch[i], fac*26%MOD, (value+val[i]*fac)%MOD); } } if (p != root) // 根节点上没有任何信息不应该被统计 vt.push_back(make_pair(value, tot)); return tot; } }; Trie Todd, Teven; void gao() { for (int i = 0; i < n; ++i) { // 处理奇数个元素构成的回文串 int pos = Todd.root, cpyi = i*2+2; int left = i-rad[cpyi]/2, right = i; for (int j = left; j <= right; ++j) { int tmp = hash.find(getkey(j, i)); if (tmp != -1) { pos = tmp; right = j-1; break; } } Todd.insert(pos, left, right, i); } hash.clear(); for (int i = 0; i < n-1; ++i) { // 处理偶数个元素构成的回文串 int pos = Teven.root, cpyi = i*2+3; int left = i-rad[cpyi]/2+1, right = i; for (int j = left; j <= right; ++j) { int tmp = hash.find(getkey(j, i)); if (tmp != -1) { pos = tmp; right = j-1; break; } } Teven.insert(pos, left, right, i); } for (int i = 0; i < m; ++i) { vt.clear(); LL K; scanf("%llu", &K); // K可能很大 for (int j = 0; j < 26; ++j) { scanf("%d", &val[j]); } Todd.cal(Todd.root, 1, 0), Teven.cal(Teven.root, 1, 0); sort(vt.begin(), vt.end()); for (int h=0; h < (int)vt.size(); ++h) { if (K > vt[h].second) { K -= vt[h].second; } else { K = 0; printf("%llu\n", vt[h].first); break; } } if (K) { // 如果总共不足K个回文串 printf("0\n"); } } puts(""); } int main() { POW[0] = 1; for (int i = 1; i < N; ++i) { POW[i] = POW[i-1]*P; } hash.init(); int T; scanf("%d", &T); while (T--) { hash.clear(); Todd.init(), Teven.init(); scanf("%d %d", &n, &m); scanf("%s", seq); sum[0] = seq[0]-'a'+1; for (int i = 1; i < n; ++i) { sum[i] = sum[i-1]*P+seq[i]-'a'+1; } // 做成一个多项式的形式 cpy[0] = '(', cpy[1] = '#'; for (int i=2,j=0; j < n; i+=2,++j) { cpy[i] = seq[j]; cpy[i+1] = '#'; } int len = n*2+3; cpy[len-1] = ')'; manacher(cpy, rad, len); // 求出每个点为中心的回文半径 gao(); } return 0; }
