ECNUOJ 2150 完美的拯救

完美的拯救

Time Limit:1000MS Memory Limit:65536KB
Total Submit:147 Accepted:50

Description 

一只可怜的蚂蚁被万恶的魔术师困在了一个魔方上, 蚁后决定委派你去拯救这只可怜的蚂蚁, 你被空投在魔方上的某个位置,你需要在最短的时间内找到那只蚂蚁, 之后使用逃离卷轴返回蚁巢,你只能在格子线上行走,并且知道被困蚂蚁的位置,你需要出色的计算来完成这项艰巨的任务.

假设魔方是3x3x3个正方体小块组成,如下图所示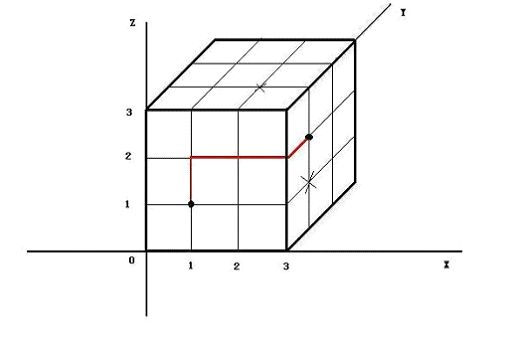


每面皆有4x4个格子道路可以行走.偶尔有些岔路点上有魔术师的魔兵把守,你不可以经过该岔路.现在以某个顶点为坐标原点建立空间坐标系,各个顶点坐标如上图所示. eg. 你被空投至(1,0,1),你要去(3,1,2), 并且(2,1,3)和(3,1,1)不可经过: 那么你可选择如下的四步路线:
(1,0,1) -> (1,0,2) -> (2,0,2) -> (3,0,2) -> (3,1,2)，(也有别的选择)

Input 

第一行有一个正整数N（1<=N<=500）,表示测试数据的组数。
对于每组测试数据：
第一行有7个整数: D, x1 y1 z1 x2 y2 z2,分别是魔方的大小,你的当前坐标以及蚂蚁的坐标(也为出口坐标);(两点均在魔方表面上).
第二行有1个整数t,表示不可经过的岔路个数.接下来t行,每行有一个坐标,是不可经过的岔路的坐标.
( 3 <= D <= 10, 0<=t<=10)

Output 

对于每组测试数据输出一个数,即最小步数,若不可到达则输出-1

Sample Input 

2
3 1 0 1 3 1 2
2
2 1 3
3 1 1
4 0 1 1 1 4 1
0

Sample Output 

4
4


Hint:
因为魔方是实体的，所以你只能在魔方的表面上行走.

Source

 

解题：无聊宽搜。。

 1 #include <bits/stdc++.h>

 2 using namespace std;

 3 struct Point {

 4     int x,y,z;

 5     int step;

 6 } start,des;

 7 int n;

 8 bool vis[20][20][20];

 9 const int dir[6][3] = {

10     0,-1,0,

11     0,1,0,

12     -1,0,0,

13     1,0,0,

14     0,0,-1,

15     0,0,1

16 };

17 queue<Point>q;

18 bool check(const Point &t) {

19     if(t.x < 0 || t.x > n || t.y < 0 || t.y > n || t.z < 0 || t.z > n) return false;

20     if(t.x > 0 && t.x < n && t.z > 0 && t.z < n && t.y > 0 && t.y < n) return false;

21     if(vis[t.x][t.y][t.z]) return false;

22     vis[t.x][t.y][t.z] = true;

23     return true;

24 }

25 int bfs() {

26     while(!q.empty()) q.pop();

27     start.step = 0;

28     q.push(start);

29     Point np;

30     vis[start.x][start.y][start.z] = true;

31     while(!q.empty()) {

32         Point now = q.front();

33         q.pop();

34         if(now.x == des.x && now.y == des.y && now.z == des.z)

35             return now.step;

36         for(int i = 0; i < 6; ++i) {

37             np.x = now.x + dir[i][0];

38             np.y = now.y + dir[i][1];

39             np.z = now.z + dir[i][2];

40             np.step = now.step + 1;

41             if(check(np)) q.push(np);

42         }

43     }

44     return -1;

45 }

46 int main() {

47     int kase,m,x,y,z;

48     scanf("%d",&kase);

49     while(kase--) {

50         scanf("%d%d%d%d",&n,&start.x,&start.y,&start.z);

51         scanf("%d%d%d",&des.x,&des.y,&des.z);

52         memset(vis,false,sizeof vis);

53         scanf("%d",&m);

54         while(m--) {

55             scanf("%d%d%d",&x,&y,&z);

56             vis[x][y][z] = true;

57         }

58         printf("%d\n",bfs());

59     }

60     return 0;

61 }

View Code