HDU 3976 Electric resistance (高斯消元法)
Electric resistance
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 326 Accepted Submission(s): 156
Problem Description
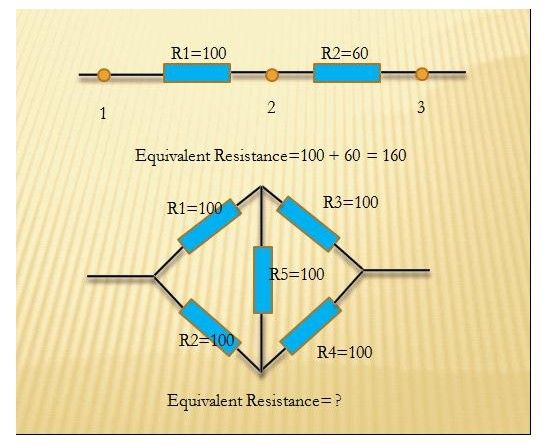
Now give you a circuit who has n nodes (marked from 1 to n) , please tell abcdxyzk the equivalent resistance of the circuit between node 1 and node n. You may assume that the circuit is connected. The equivalent resistance of the circuit between 1 and n is that, if you only consider node 1 as positive pole and node n as cathode , all the circuit could be regard as one resistance . (It's important to analyse complicated circuit ) At most one resistance will between any two nodes.

Input
In the first line has one integer T indicates the number of test cases. (T <= 100)
Each test first line contain two number n m(1<n<=50,0<m<=2000), n is the number of nodes, m is the number of resistances.Then follow m lines ,each line contains three integers a b c, which means there is one resistance between node a and node b whose resistance is c. (1 <= a,b<= n, 1<=c<=10^4) You may assume that any two nodes are connected!
Each test first line contain two number n m(1<n<=50,0<m<=2000), n is the number of nodes, m is the number of resistances.Then follow m lines ,each line contains three integers a b c, which means there is one resistance between node a and node b whose resistance is c. (1 <= a,b<= n, 1<=c<=10^4) You may assume that any two nodes are connected!
Output
for each test output one line, print "Case #idx: " first where idx is the case number start from 1, the the equivalent resistance of the circuit between 1 and n. Please output the answer for 2 digital after the decimal point .
Sample Input
1 4 5 1 2 1 2 4 4 1 3 8 3 4 19 2 3 12
Sample Output
Case #1: 4.21
Author
abcdxyzk
Source
高斯消元解方程组。
主要是方程的建立。
我建方程使用了n个未知数,表示n个点的电势。
需要列n个方程。
就根据n个点,流入电流等于流出电流,或者说每个点电流之和(假如流入为正,流出为负,反之也可)
这样可以列出n个方程,根据n个点电流和为0.
而且可以假设1这个点流入电流为-1, 这样设点电势为0,那么可以知道n这个点的电势就等于等效电阻了、。
流入肯定等于流出的,上面列的方程组中第n个的是多余的,可以去掉,替换成1点电压为0.
这样方程组正确建立。
对于u ----> v 电阻为w. 可以知道u加一个电流 xv/w - xu/w. 而v加一个电流 xu/w - xv/w;
1 /* *********************************************** 2 Author :kuangbin 3 Created Time :2013-11-17 23:18:47 4 File Name :E:\2013ACM\比赛练习\2013-11-17\EE.cpp 5 ************************************************ */ 6 7 #include <stdio.h> 8 #include <string.h> 9 #include <iostream> 10 #include <algorithm> 11 #include <vector> 12 #include <queue> 13 #include <set> 14 #include <map> 15 #include <string> 16 #include <math.h> 17 #include <stdlib.h> 18 #include <time.h> 19 using namespace std; 20 const double eps = 1e-9; 21 const int MAXN = 100; 22 double a[MAXN][MAXN],x[MAXN]; 23 int equ,var; 24 int Gauss() 25 { 26 int i,j,k,col,max_r; 27 for(k = 0,col = 0;k < equ && col < var;k++,col++) 28 { 29 max_r = k; 30 for(i = k+1;i < equ;i++) 31 if(fabs(a[i][col]) > fabs(a[max_r][col])) 32 max_r = i; 33 if(fabs(a[max_r][col]) < eps)return 0; 34 if(k != max_r) 35 { 36 for(j = col;j < var;j++) 37 swap(a[k][j],a[max_r][j]); 38 swap(x[k],x[max_r]); 39 } 40 x[k]/=a[k][col]; 41 for(j = col+1;j < var;j++)a[k][j]/=a[k][col]; 42 a[k][col] = 1; 43 for(int i = 0;i < equ;i++) 44 if(i != k) 45 { 46 x[i] -= x[k]*a[i][k]; 47 for(j = col+1;j < var;j++)a[i][j] -= a[k][j]*a[i][col]; 48 a[i][col] = 0; 49 } 50 } 51 return 1; 52 } 53 int main() 54 { 55 //freopen("in.txt","r",stdin); 56 //freopen("out.txt","w",stdout); 57 int n,m; 58 int T; 59 int iCase = 0; 60 scanf("%d",&T); 61 while(T--) 62 { 63 iCase++; 64 scanf("%d%d",&n,&m); 65 equ = var = n; 66 memset(a,0,sizeof(a)); 67 int u,v,w; 68 for(int i = 0;i < m;i++) 69 { 70 scanf("%d%d%d",&u,&v,&w); 71 a[u-1][v-1] += 1.0/w; 72 a[u-1][u-1] += -1.0/w; 73 a[v-1][u-1] += 1.0/w; 74 a[v-1][v-1] += -1.0/w; 75 } 76 for(int i = 0;i < n-1;i++) 77 x[i] = 0; 78 x[0] = 1; 79 for(int i = 0;i < n;i++) 80 a[n-1][i] = 0; 81 x[n-1] = 0; 82 a[n-1][0] = 1; 83 Gauss(); 84 printf("Case #%d: %.2lf\n",iCase,x[n-1]); 85 } 86 return 0; 87 }
第一次写的时候用n+m个未知数做的,也可以A掉,但是有m个变量多余了。