《大话数据结构》1、2数据结构、算法
大话数据结构
大话设计模式
head first设计模式
Java核心技术 卷1
深入理解Java虚拟机(JVM高级特性与最佳实践)
图解HTTP
大话数据结构
数据结构介绍,
算法推导大O阶的方法,
线性表结构的介绍,顺序结构与链式结构差异,
栈与队列的应用,
串的朴素模式匹配、 KMP 模式匹配算法,
树结构的介绍, 二叉树前中后序遍历,线索二叉树,赫夫曼树及应用,
图结掏的介绍,图的深度、广度遍历,最小生成树两种算法,最短路径两种算法,拓扑排序与关键路径算法,
查找应用的相关介绍,折半查找、插值查找、斐被那契查找等静态查拢,稠密索引、分块索引、倒排索引等索引技术, 二叉排序树、平衡二叉树等动态查找, 8 树、 B+树技术、 散列表技术,
排序应用的相关介绍,冒泡、选择、插入等简单排序, 希尔、堆、归井、快速等改进排序,各位排序算法的对比等。
共九章:数据结构、算法、线性表、栈与队列、串、树、图、查找、排序
目录 · · · · · ·
第1章数据结构绪论 1
1.1开场白 2
如果你交给某人一个程序,你将折磨他一整天;如果你教某人如何编写程序,你将折磨他一辈子。
1.2你数据结构怎么学的? 3
他完成开发并测试通过后,得意地提交了代码。项目经理看完代码后拍着桌子对他说:“你数据结构是怎么学的?”
1.3数据结构起源 4
1.4基本概念和术语 5
正所谓“巧妇难为无米之炊”,再强大的计算机,也要有“米”下锅才可以干活,否则就是一堆破铜烂铁。这个“米”就是数据。
1.4.1数据 5
1.4.2数据元素 5
1.4.3数据项 6
1.4.4数据对象 6
1.4.5数据结构 6
1.5逻辑结构与物理结构 7
1.5.1逻辑结构 7
1.5.2物理结构 9
1.6抽象数据类型 11
大家都需要房子住,但显然没钱考虑大房子是没有意义的。于是商品房就出现了各种各样的户型,有几百平米的别墅,也有仅两平米的胶囊公寓……
1.6.1数据类型 11
.1.6.2抽象数据类型 12
1.7总结回顾 14
1.8结尾语 15
最终的结果一定是,你对着别人很牛的说“数据结构——就那么回事。”
第2章算法 17
2.1开场白 18
2.2数据结构与算法关系 18
计算机界的前辈们,是一帮很牛很牛的人,他们使得很多看似没法解决或者很难解决的问题,变得如此美妙和神奇。
2.3两种算法的比较 19
高斯在上小学的一天,老师要求每个学生都计算1+2+…+100的结果,谁先算出来谁先回家……
2.4算法定义 20
现实世界中的算法千变万化,没有通用算法可以解决所有问题。甚至一个小问题,某个解决此类问题很优秀的算法却未必就适合它。
2.5算法的特性 21
2.5.1输入输出 21
2.5.2有穷性 21
2.5.3确定性 21
2.5.4可行性 21
2.6算法设计的要求 22
求100个人的高考成绩平均分与求全省所有考生的成绩平均分在占用时间和内存存储上有非常大的差异,我们自然追求高效率和低存储的算法来解决问题。
2.6.1正确性 22
2.6.2可读性 23
2.6.3健壮性 23
2.6.4时间效率高和存储量低 23
2.7算法效率的度量方法 24
随着n值越来越大,它们在时间效率上的差异也就越来越大。好比有些人每天都在学习,而另一些人,打打游戏、睡睡大觉,毕业后前者名企争着要,后者求职处处无门。
2.7.1事后统计方法 24
2.7.2事前分析估算方法 25
2.8函数的渐近增长 27
2.9算法时间复杂度 29
理解大o推导不算难,难的其实是对数列的一些相关运算,这考察的更多的是数学知识和能力。
2.9.1算法时间复杂度定义 29
2.9.2推导大o阶方法 30
2.9.3常数阶 30
2.9.4线性阶 31
2.9.5对数阶 32
2.9.6平方阶 32
2.10常见的时间复杂度 35
有些时候,告诉你某些东西不可以去尝试,也是一种知识的传递。总不能非要去被毒蛇咬一口才知道蛇不可以去招惹吧。
2.11最坏情况与平均情况 35
2.12算法空间复杂度 36
事先建立一个有2050大的数组,然后把所有年份按下标数字对应,如果是闰年,此数组项的值就是1,如果不是就是0。这样,所谓的判断某一年是否是闰年就变成了查找这个数组的某一项的值是多少的问题。
2.13总结回顾 37
2.14结尾语 38
愚公移山固然可敬,但发明炸药和推土机,可能更加实在和聪明。
第3章线性表 41
3.1开场白 42
门外家长都挤在大门口与门里的小孩子的井然有序,形成了鲜明对比。哎,有时大人的所作所为,其实还不如孩子。
3.2线性表的定义 42
3.3线性表的抽象数据类型 45
有时我们想知道某个小朋友(比如麦兜)是否是班级的同学,老师会告诉我说,没有,麦兜是在春田花花幼儿园里。这种查找某个元素是否存在的操作很常用。
3.4线性表的顺序存储结构 47
他每次一吃完早饭就冲着去了图书馆,挑一个好地儿,把他书包里的书,一本一本的按座位放好,长长一排,九个座硬是被他占了。
3.4.1顺序存储定义 47
3.4.2顺序存储方式 47
3.4.3数据长度与线性表长度区别 48
3.4.4地址计算方法 49
3.5顺序存储结构的插入与删除 50
春运时去买火车票,大家都排队排着好好的,这时来了一个美女:“可否让我排在你前面?”这可不得了,后面的人像蠕虫一样,全部都得退后一步。
3.5.1获得元素操作 50
3.5.2插入操作 51
3.5.3删除操作 52
3.5.4线性表顺序存储结构的优缺点 54
3.6线性表的链式存储结构 55
反正也是要让相邻元素间留有足够余地,那干脆所有元素都不要考虑相邻位置了,哪有空位就到哪里。而只是让每个元素知道它下一个元素的位置在哪里。
3.6.1顺序存储结构不足的解决
办法 55
3.6.2线性表链式存储结构定义 56
3.6.3头指针与头结点的异同 58
3.6.4线性表链式存储结构代码描述 58
3.7单链表的读取 60
3.8单链表的插入与删除 61
本来是爸爸左牵着妈妈的手、右牵着宝宝的手在马路边散步。突然迎面走来一美女,爸爸失神般地望着,此情景被妈妈逮个正着,于是扯开父子俩,拉起宝宝的左手就快步朝前走去。
3.8.1单链表的插入 61
3.8.2单链表的删除 64
3.9单链表的整表创建 66
3.10单链表的整表删除 69
3.11单链表结构与顺序存储结构优缺点 70
3.12静态链表 71
对于一些语言,如basic、fortran等早期的编程高级语言,由于没有指针,这链表结构,按照前面我们的讲法,它就没法实现了。怎么办呢?
3.12.1静态链表的插入操作 73
3.12.2静态链表的删除操作 75
3.12.3静态链表优缺点 77
3.13循环链表 78
这个轮回的思想很有意思。它强调了不管你今生是穷是富,如果持续行善积德,下辈子就会好过,反之就会遭到报应。
3.14双向链表 81
就像每个人的人生一样,欲收获就得付代价。双向链表既然是比单链表多了如可以反向遍历查找等的数据结构,那么也就需要付出一些小的代价。
3.15总结回顾 84
3.16结尾语 85
如果你觉得上学读书是受罪,假设你可以活到80岁,其实你最多也就吃了20年苦。用人生四分之一的时间来换取其余时间的幸福生活,这点苦不算啥。
第4章栈与队列 87
4.1开场白 88
想想看,在你准备用枪的时候,突然这手枪明明有子弹却打不出来,这不是要命吗。
4.2栈的定义 89
类似的很多软件,比如word、photoshop等,都有撤消(undo)的操作,也是用栈这种思想方式来实现的。
4.2.1栈的定义 89
4.2.2进栈出栈变化形式 90
4.3栈的抽象数据类型 91
4.4栈的顺序存储结构及实现 92
4.4.1栈的顺序存储结构 92
4.4.2栈的顺序存储结构进栈操作 93
4.4.3栈的顺序存储结构出栈操作 94
4.5两栈共享空间 94
两个大学室友毕业同时到北京工作,他们都希望租房时能找到独自住的一室户或一室一厅,可找来找去发现,实在是承受不起。
4.6栈的链式存储结构及实现 97
4.6.1栈的链式存储结构 97
4.6.2栈的链式存储结构进栈操作 98
4.6.3栈的链式存储结构出栈操作 99
4.7栈的作用 100
4.8栈的应用——递归 100
当你往镜子前面一站,镜子里面就有一个你的像。但你试过两面镜子一起照吗?如果a、b两面镜子相互面对面放着,你往中间一站,嘿,两面镜子里都有你的千百个“化身”。
4.8.1斐波那契数列实现 101
4.8.2递归定义 103
4.9栈的应用——四则运算表达式求值 104
4.9.1后缀(逆波兰)表示法定义 104
4.9.2后缀表达式计算结果 106
4.9.3中缀表达式转后缀表达式 108
4.10队列的定义 111
电脑有时会处于疑似死机的状态。就当你失去耐心,打算了reset时。突然它像酒醒了一样,把你刚才点击的所有操作全部都按顺序执行了一遍。
4.11队列的抽象数据类型 112
4.12循环队列 113
你上了公交车发现前排有两个空座位,而后排所有座位都已经坐满,你会怎么做?立马下车,并对自己说,后面没座了,我等下一辆?没这么笨的人,前面有座位,当然也是可以坐的。
4.12.1队列顺序存储的不足 112
4.12.2循环队列定义 114
4.13队列的链式存储结构及实现 117
4.13.1队列链式存储结构入队操作118
4.13.2队列链式存储结构出队操作 119
4.14总结回顾 120
4.15结尾语 121
人生,需要有队列精神的体现。南极到北极,不过是南纬90度到北纬90度的队列,如果你中途犹豫,临时转向,也许你就只能和企鹅相伴永远。可事实上,无论哪个方向,只要你坚持到底,你都可以到达终点。
第5章串 123
5.1开场白 124
“枯眼望遥山隔水,往来曾见几心知?壶空怕酌一杯酒,笔下难成和韵诗。途路阻人离别久,讯音无雁寄回迟。孤灯夜守长寥寂,夫忆妻兮父忆儿。”……可再仔细一读发现,这首诗竟然可以倒过来读。
5.2串的定义 124
我所提到的“over”、“end”、“lie”其实就是“lover”、“friend”、“believe”这些单词字符串的子串。
5.3串的比较 126
5.4串的抽象数据类型 127
5.5串的存储结构 128
感情上发生了问题,为了向女友解释一下,我准备发一条短信,一共打了75个字。最后八个字是“我恨你是不可能的”,点发送。后来得知对方收到的,只有70个字,短信结尾是“……我恨你”。
5.5.1串的顺序存储结构 129
5.5.2串的链式存储结构 131
5.6朴素的模式匹配算法 131
主串为s=”00000000000000000000000000000000000000000000000001”,而要匹配的子串为t=”0000000001”,……在匹配时,每次都得将t中字符循环到最后一位才发现,哦,原来它们是不匹配的。
5.7kmp模式匹配算法 135
很多年前我们的科学家觉得像这种有多个0和1重复字符的字符串,却需要挨个遍历的算法,是非常糟糕的事情。
5.7.1kmp模式匹配算法原理 135
5.7.2next数组值推导 139
5.7.3kmp模式匹配算法实现 141
5.7.4kmp模式匹配算法改进 142
5.7.5nextval数组值推导 144
5.8总结回顾 146
5.9结尾语 146
《璇玑图》共八百四十字,纵横各二十九字,纵、横、斜、交互、正、反读或退一字、迭一字读均可成诗,诗有三、四、五、六、七言不等,目前有人统计可组成七千九百五十八首诗。听清楚哦,是7958首。
第6章树 149
6.1开场白 150
无论多高多大的树,那也是从小到大的,由根到叶,一点点成长起来的。俗话说十年树木,百年树人,可一棵大树又何止是十年这样容易。
6.2树的定义 150
树的定义其实就是我们在讲解栈时提到的递归的方法。也就是在树的定义之中还用到了树的概念,这是比较新的一种定义方法。
6.2.1结点分类 152
6.2.2结点间关系 152
6.2.3树的其他相关概念 153
6.3树的抽象数据类型 154
6.4树的存储结构 155
6.4.1双亲表示法 155
6.4.2孩子表示法 158
6.4.3孩子兄弟表示法 162
6.5二叉树的定义 163
苏东坡曾说:“人有悲欢离合,月有阴晴圆缺,此事古难全”。意思就是完美是理想,不完美才是人生。我们通常举的例子也都是左高右低、参差不齐的二叉树。那是否存在完美的二叉树呢?
6.5.1二叉树特点 164
6.5.2特殊二叉树 166
6.6二叉树的性质 169
6.6.1二叉树性质1 169
6.6.2二叉树性质2 169
6.6.3二叉树性质3 169
6.6.4二叉树性质4 170
6.6.5二叉树性质5 171
6.7二叉树的存储结构 172
6.7.1二叉树顺序存储结构 172
6.7.2二叉链表 173
6.8遍历二叉树 174
你人生的道路上,高考填志愿要面临哪个城市、哪所大学、具体专业等选择,由于选择方式的不同,遍历的次序就完全不同。
6.8.1二叉树遍历原理 174
6.8.2二叉树遍历方法 175
6.8.3前序遍历算法 178
6.8.4中序遍历算法 181
6.8.5后序遍历算法 184
6.8.6推导遍历结果 184
6.9二叉树的建立 187
6.10线索二叉树 188
我们现在提倡节约型社会,一切都应该节约为本。对待我们的程序当然也不例外,能不浪费的时间或空间,都应该考虑节省。
6.10.1线索二叉树原理 188
6.10.2线索二叉树结构实现 191
6.11树、森林与二叉树的转换 195
有个乡镇企业也买了同样的生产线,老板发现这个问题后找了个小工来说:你必须搞定,不然炒你鱿鱼。小工很快想出了办法:他在生产线旁边放了台风扇猛吹,空皂盒自然会被吹走。
6.11.1树转换为二叉树 196
6.11.2森林转换为二叉树 197
6.11.3二叉树转换为树 197
6.11.4二叉树转换为森林 199
6.11.5树与森林的遍历 199
6.12赫夫曼树及其应用 200
压缩而不出错是如何做到的呢?简单的说,就是把我们要压缩的文本进行重新编码,以达到减少不必要的空间的技术。压缩和解压缩技术就是基于赫夫曼的研究之上发展而来,我们应该记住他。
6.12.1赫夫曼树 200
6.12.2赫夫曼树定义与原理 203
6.12.3赫夫曼编码 205
6.13总结回顾 208
6.14结尾语 209
人受伤时会流下泪水。树受伤时,天将再不会哭。希望我们的未来不要仅仅是钢筋水泥建造的高楼,也要有那郁郁葱葱的森林和草地,我们人类才可能与自然和谐共处。
第7章图 211
7.1开场白 212
如果你不善于规划,很有可能就会出现如玩好新疆后到海南,然后再冲向黑龙江这样的荒唐决策。
7.2图的定义 213
现实中,人与人之间关系就非常复杂,比如我的认识的朋友,可能他们之间也互相认识,这就不是简单的一对一、一对多的关系了,那就是我们今天要研究的主题——图。
7.2.1各种图定义 214
7.2.2图的顶点与边间关系 217
7.2.3连通图相关术语 219
7.2.4图的定义与术语总结 222
7.3图的抽象数据类型 222
7.4图的存储结构 223
因为美国的黑夜就是中国的白天,利用互联网,他的员工白天上班就可以监控到美国仓库夜间的实际情况,如果发生了像火灾、偷盗这样的突发事件,及时电话到美国当地相关人员处理
7.4.1邻接矩阵 224
7.4.2邻接表 228
7.4.3十字链表 232
7.4.4邻接多重表 234
7.4.5边集数组 236
7.5图的遍历 237
我有一天早晨准备出门,发现钥匙不见了。一定是我儿子拿着玩,不知道丢到哪个犄角旮旯去了,你们说,我应该如何找?
7.5.1深度优先遍历 238
7.5.2广度优先遍历 242
7.6最小生成树 245
如果你加班加点,没日没夜设计出的结果是方案一,我想你离被炒鱿鱼应该是不远了(同学微笑)。因为这个方案比后两个方案一半还多的成本会让老板气晕过去的。
7.6.1普里姆(prim)算法 247
7.6.2克鲁斯卡尔(kruskal)算法 251
7.7最短路径 257
有人为了省钱,需路程最短,但换乘站间距离长等原因并不省时间;另一些人,他为赶时间,最大的需求是总时间要短;还有一类人,他们都不想多走路,关键是换乘要少,这样可以在车上好好休息一下。
7.7.1迪杰斯特拉(dijkstra)算法 259
7.7.3弗洛伊德(floyd)算法 265
7.8拓扑排序 270
电影制作不可能在人员到位进驻场地时,导演还没有找到,也不可能在拍摄过程中,场地都没有。这都会导致荒谬的结果。
7.8.1拓扑排序介绍 271
7.8.2拓扑排序算法 272
7.9关键路径 277
假如造一个轮子要0.5天、造一个发动机要3天、造一个车底盘要2天、造一个外壳要2天,其它零部件2天,全部零部件集中到一处要0.5天,组装成车要2天,请问,在汽车厂造一辆车,最短需要多少天呢?
7.9.1关键路径算法原理 279
7.9.2关键路径算法 280
7.10总结回顾 287
7.11结尾语 289
世界上最遥远的距离,不是牛a与牛c之间狭小空隙,而是你们当中,有人在通往牛逼的路上一路狂奔,而有人步入大学校园就学会放弃。
第8章查找 291
8.1开场白 292
当你精心写了一篇博文或者上传一组照片到互联网上,来自世界各地的无数“蜘蛛”便会蜂拥而至。所谓蜘蛛就是搜索引擎公司服务器上软件,它把互联网当成了蜘蛛网,没日没夜的访问上面的各种信息。
8.2查找概论 293
比如网络时代的新名词,如“蜗居”、“蚁族”等,如果需要将它们收录到汉语词典中,显然收录时就需要查找它们是否存在,以及找到如果不存在时应该收录的位置。
8.3顺序表查找 295
8.3.1顺序表查找算法 296
8.3.2顺序表查找优化 297
8.4有序表查找 298
我在纸上已经写好了一个100以内的正整数请你猜,问几次可以猜出来。当时已经介绍了如何才可以最快的猜出这个数字。我们把这种每次取中间记录查找的方法叫做折半查找。
8.4.1折半查找 298
8.4.2插值查找 301
8.4.3斐波那契查找 302
8.5线性索引查找 306
我母亲年纪大了,经常在家里找不到东西,于是她用一小本子,记录了家里所有小东西放置的位置,比如户口本放在右手床头柜下面抽屉中,钞票放在衣……咳,这个就不提了。
8.5.1稠密索引 307
8.5.2分块索引 308
8.5.3倒排索引 311
8.6二叉排序树 313
后来老虎来了,一人拼命地跑,另一人则急中生智,爬到了树上。而老虎是不会爬树的,结果……。爬树者改变了跑的思想,这一改变何等重要,捡回了自己的一条命。
8.6.1二叉排序树查找操作 316
8.6.2二叉排序树插入操作 318
8.6.3二叉排序树删除操作 320
8.6.4二叉排序树总结 327
8.7平衡二叉树(avl树) 328
平板就是一个世界,当诱惑降临,人心中的平衡被打破,世界就会混乱,最后留下的只有孤独寂寞失败。这种单调的机械化的社会,禁不住诱惑的侵蚀,最容易被侵蚀的,恰恰是最空虚的心灵。
8.7.1平衡二叉树实现原理 330
8.7.2平衡二叉树实现算法 334
8.8多路查找树(b树) 341
要观察一个公司是否严谨,看他们如何开会就知道了。如果开会时每一个人都只是带一张嘴,即兴发言,这肯定是一家不严谨的公司。
8.8.12-3树 343
8.8.22-3-4树 348
8.8.3b树 349
8.8.4b+树 351
8.9散列表查找(哈希表)概述 353
你很想学太极拳,听说学校有个叫张三丰的人打得特别好,于是到学校学生处找人,工作人员拿出学生名单,最终告诉你,学校没这个人,并说张三丰几百年前就已经在武当山作古了。
8.9.1散列表查找定义 354
8.9.2散列表查找步骤 355
8.10散列函数的构造方法 356
8.10.1直接定址法 357
8.10.2数字分析法 358
8.10.3平方取中法 359
8.10.4折叠法 359
8.10.5除留余数法 359
8.10.6随机数法 360
8.11处理散列冲突的方法 360
我们每个人都希望身体健康,虽然疾病可以预防,但不可避免,没有任何人可以说,生下来到现在没有生过一次病。
8.11.1开放定址法 361
8.11.2再散列函数法 363
8.11.3链地址法 363
8.11.4公共溢出区法 364
8.12散列表查找实现 365
8.12.1散列表查找算法实现 365
8.12.2散列表查找性能分析 367
8.13总结回顾 368
8.14结尾语 369
如果我是个喜欢汽车的人,时常搜汽车信息。那么当我在搜索框中输入“甲壳虫”、“美洲虎”等关键词时,不要让动物和人物成为搜索的头条。
第9章排序 373
9.1开场白 374
假如我想买一台iphone4的手机,于是上了某电子商务网站去搜索。可搜索后发现,有8863个相关的物品,如此之多,这叫我如何选择。我其实是想买便宜一点的,但是又怕遇到骗子,想找信誉好的商家,如何做?
9.2排序的基本概念与分类 375
比如我们某些大学为了选拔在主科上更优秀的学生,要求对所有学生的所有科目总分倒序排名,并且在同样总分的情况下将语数外总分做倒序排名。这就是对总分和语数外总分两个次关键字的组合排序。
9.2.1排序的稳定性 376
9.2.2内排序与外排序 377
9.2.3排序用到的结构与函数 378
9.3冒泡排序 378
无论你学习哪种编程语言,在学到循环和数组时,通常都会介绍一种排序算法,而这个算法一般就是冒泡排序。并不是它的名称很好听,而是说这个算法的思路最简单,最容易理解。
9.3.1最简单排序实现 379
9.3.2冒泡排序算法 380
9.3.3冒泡排序优化 382
9.3.4冒泡排序复杂度分析 383
9.4简单选择排序 384
还有一种做股票的人,他们很少出手,只是在不断观察和判断,等时机一到,果断买进或卖出。他们因为冷静和沉着,以及交易的次数少,而最终收益颇丰。
9.4.1简单选择排序算法 384
9.4.2简单选择排序复杂度分析 385
9.5直接插入排序 386
哪怕你是第一次玩扑克牌,只要认识这些数字,理牌的方法都是不用教的。将3和4移动到5的左侧,再将2移动到最左侧,顺序就算是理好了。这里,我们的理牌方法,就是直接插入排序法。
9.5.1直接插入排序算法 386
9.5.2直接插入排序复杂度分析 388
9.6希尔排序 389
不管怎么说,希尔排序算法的发明,使得我们终于突破了慢速排序的时代(超越了时间复杂度为o(n2)),之后,更为高效的排序算法也就相继出现了。
9.6.1希尔排序原理 391
9.6.2希尔排序算法 391
9.6.3希尔排序复杂度分析 395
9.7堆排序 396
什么叫堆结构呢?回忆一下我们小时候,特别是男同学,基本都玩过叠罗汉的恶作剧。通常都是先把某个要整的人按倒在地,然后大家就一拥而上扑了上去……后果?后果当然就是一笑了之。
9.7.1堆排序算法 398
9.7.2堆排序复杂度分析 405
9.8归并排序 406
即使你是你们班级第一、甚至年级第一名,如果你没有上分数线,则说明你的成绩排不到全省前1万名,你也就基本失去了当年上本科的机会了。
9.8.1归并排序算法 407
9.8.2归并排序复杂度分析 413
9.8.3非递归实现归并排序 413
9.9快速排序 417
终于我们的高手要登场了,将来你工作后,你的老板让你写个排序算法,而你会的算法中竟然没有快速排序,我想你还是不要声张,偷偷去把快速排序算法找来敲进电脑,这样至少你不至于被大伙儿取笑。
9.9.1快速排序算法 417
9.9.2快速排序复杂度分析 421
9.9.3快速排序优化 422
9.10总结回顾 428
目前还没有十全十美的排序算法,有优点就会有缺点,即使是快速排序法,也只是在整体性能上优越,它也存在排序不稳定、需要大量辅助空间、对少量数据排序无优势等不足。
9.11结尾语 430
如果你有梦想的话,就要去捍卫它。当别人做不到的时候,他们就想要告诉你,你也不能。如果你想要些什么,就得去努力争取。就这样!
附录参考文献 435
第1章数据结构绪论 1
数据结构;是相互之间存在一种或多种特定关系的数据元素的集合。
1.1开场白 2
如果你交给某人一个程序,你将折磨他一整天;如果你教某人如何编写程序,你将折磨他一辈子。
1.2你数据结构怎么学的? 3
他完成开发并测试通过后,得意地提交了代码。项目经理看完代码后拍着桌子对他说:“你数据结构是怎么学的?”
工作中,有一次他们需要开发一个客服电话系统,他们项目经理安排小菜完成客 户排队模块的代码工作。
小菜觉得这个很容易,用数据库设计了一张客户排队衰,并且用一个自动递增的 整型数字作为客户的编号。只要来一个客户,就给这张表的末尾插入一条数据。等客 服系统一有空闲,就从这张表中取出最小编号的客户提交,并且删除这条记录。
这种实时的排队模块,用什么数据库呀,在内存中完成不就行了吗
这种实时的排队系统,通常用数据结构中的队列结构是比较好的,用数组虽然也可以,但是又要考虑溢出,又要考虑新增和删除后的数据移动,总的说来很不方便。
在工作中发现,我所需要的如栈、队列、链表、 散列表等结构,以及查找、 排序等算法,在编程语言的开发工具包中都有完美的实现,我只需要掌握如何使用它们就可以了,为什么还要去弄懂这里面的算法原理呢?
1.3数据结构起源 4
早期人们都把计算机理解为数值计算工具,就是感觉计算机当然是用来计算的, 所以计算机解决问题,应该是先从具体间题中抽象出一个适当的数据模型,设计出一 个解此数据模型的算法,然后再编写程序,得到一个实际的软件。
可现实中, 我们更多的不是解决数值计算的问题,而是需要一些更科学有效的手段(比如表、树和图等数据结构)的帮助,才能更好地处理问题。 所以数据结构是一 门研究非数值计算的程序设计问题中的操作对象,以及他们之间的关系和操作等相关问题的学科。
1968 年,美国的高德纳 (Donakl E. Knuth) 教授在其所写的 《计算机程序的f艺 术》 第一卷 《基本算法》 中,较系统地阐述了数据的逻辑结构和存储结构及其操作, 开创了数据结构的课程体系。
之后, 70年代初,出现了大型程序,软件也开始相对独立,结构程序设计成为程序设计方法学的主要内容,人们越来越重视"数据结构,认为程序设计的实质是对确定的问题选择一种好的结构,加上设计一种好的算法。可见,数据结构在程序设计当 中占据了重要的地位。
程序设计 = 数据结构+算法
1.4基本概念和术语 5
正所谓“巧妇难为无米之炊”,再强大的计算机,也要有“米”下锅才可以干活,否则就是一堆破铜烂铁。这个“米”就是数据。
1.4.1数据 5
数据:是描述客观事物的符号,是计算机中可以操作的对象,是能被计算机识别,并输入给计算机处理的符号集合。 数据不仅仅包括整型、实型等数值类型,还包括字符及声音、图像、视频等非数值类型。而声音、图像、视频等其实i是可以通过编码的手段变成字符数据来处理的。
1.4.2数据元素 5
数据元素:是组成数据的、有一定意义的基本单位,在计算机中通常作为整体处理,也被称为记录
1.4.3数据项 6
数据项:一个数据元素可以由若干个数据项组成,数据项是数据不可分割的最小单位
1.4.4数据对象 6
数据对象:是性质相同的数据元素的集合,是数据的子集
1.4.5数据结构 6
不同数据元素之间不是独立的,而是存在特定的关系,我们将这些关系称为结构
数据结构:是相互之间存在一种或多种特定关系的数据元素的集合
为编写出一个好的程序,必须分析待处理对象的特性及各处理对象之间存在的关系。这也就是研究数据结构的意义所在。
1.5逻辑结构与物理结构 7
1.5.1逻辑结构 7
逻辑结构:是指数据对象中数据元素之间的相互关系
集合结构
集合结构:集合结构中的数据元素除了同属于一个集合外,它们之间没有其他关系。各个数据元素是”平等”的,类似于数学中的集合
线性结构
线性结构:线性结构中的数据元素之间是一对一的关系
树形结构
树形结构:树形结构中的数据元素之间存在一种一对多的层次关系
图形结构
图形结构:图形结构的数据元素是多对多的关系
逻辑结构是针对具体问题的,是为了解决某个问题, 在对问题理解的基础上,选择一个合适的数据结构表示数据元素之间的逻辑关系。
1.5.2物理结构 9
物理结构(存储结构):是指数据的逻辑结构在计算机中的存储形式.存储器主要是针对内存而言的,像硬盘、软盘、光盘等外 部存俯器的数据组织通常用文件结构来描述。
数据的存储结构应正确反映数据元素之间的逻辑关系,这才是最为关键的,如何 存储数据元素之间的逻辑关系,是实现物理结构的重点和难点。
顺序存储结构
顺序存储结构:是把数据元素存放在地址连续的存储单元里,其数据间的逻辑关系和物理关系是一致的
面对这样时常要变化的结构,顺序存储是不科学的。
链式存储结构
链式存储结构:是把数据元素存放在任意的存储单元里,这组存储单元可以是连续的,也可以是不连续的,数据元素的存储关系并不能反映其逻辑关系,因此需要用一个指针存放数据元素的地址,这样通过地址就可以找到相关数据元素的位置
显然,链式存储就灵活多了,数据存在哪里不重要,只要有一个指针存放了相应 的地址就能找到它了。
逻辑结构是面向问题的,而物理结构就是面向计算机的,其基本的目标就是将数 据及其逻辑关系存储到计算机的内存中。
1.6抽象数据类型 11
大家都需要房子住,但显然没钱考虑大房子是没有意义的。于是商品房就出现了各种各样的户型,有几百平米的别墅,也有仅两平米的胶囊公寓……
1.6.1数据类型 11
数据类型:是指一组性质相同的值的集合及定义在此集合上的一些操作的总称
数据类型是按照值的不同进行划分的。在高级语言中,每个变量、常量和表达式都有各自的取值范围。类型就用来说明变量或表达式的取值范围和所能进行的操作。
在C语言中,按照取值的不同,数据类型可以分为两类
原子类型
是不可以再分解的基本类型,包括整型、字符型等
结构类型
由若干个类型组合而成,是可以再分解的,例如整型数组
因为不同的计算机有不同的硬件系统,这就要求程序语言最终通过编译器或解释器转换成底层语言,如汇编语言甚至是通过机器语言的数据类型来实现的。可事实 上,高级语言的编程者不管最终程序运行在什么计算机上,他的目的就是为了实现两 个整型数字的运算,如 a+b、 a-b、 axb 和 a/b 等,他才不关心整数在计算机内部是如 何表示的 , 也不想知道 CPU 为了实现 1+2 进行几次开关操作,这些操作是如何实现 的,对高级语言开发者来讲根本不重要。于是我们就会考虑,无论什么计算机、什么 计算机语言,大都会面临着如整数运算、实数运算、字符运算等操作,我们可以考虑把它们都抽象出来。
抽象是指抽取出事物具有的普遍性的本质。它是抽出问题的特征而忽略非本质的细节,是对具体事物的一个概括。抽象是一种思考问题的方式,它隐藏了繁杂的细节,只保留实现目标所必需的信息。
1.6.2抽象数据类型 12
抽象数据类型(Abstract Data Type, ADT):是指一个数学模型及定义在该模型上的一组操作,如”整数”类型->整型
抽象数据类型的定义仅取决于它的一组逻辑特性,而与其在计算机内 部如何表示和实现无关。
一个抽象数据类型定义了 : 一个数据对象、数据对象中各数据元素之间的关系及对数据元素的操作。至于,一个 抽象数据类型到底需要哪些操作,这就只能由设计者根据实际需要来定。
抽象数据类型体现了程序设计中问题分解、抽象和信息隐藏的特性。。抽 象数据类型把实际生活中的问题分解为多个规模小且窑易处理的问题, 然后建立一个 计算机能处理的数据模型,并把每个功能模块的实现细节作为一个独立的单元,从而 使具体实现过程隐藏起来。
描述抽象数据类型的标准格式:
ADT 抽象数据类型名
Data
数据元素之间逗得关系的定义
Operation
操作 1
初始条件
操作结来描述
操作 2
操作 n
endADT
1.7总结回顾 14
1.8结尾语 15
最终的结果一定是,你对着别人很牛的说“数据结构——就那么回事。”
学会游泳难吗?掌握英语口语难吗?可能是难,但在 掌握了的人眼里,这根本不算什么,“就那么回事呀”。只要你相信自己一定可以学得 会、学得好,既然无数人已经掌握了,你凭什么不行。
第2章算法 17
算法:算法是解决特定问题求解步骤的描述, 在计算机中表现为指令的有限序列, 并且每条指令表示一个或多个操作。
2.1开场白 18
2.2数据结构与算法关系 18
计算机界的前辈们,是一帮很牛很牛的人,他们使得很多看似没法解决或者很难解决的问题,变得如此美妙和神奇。
"数据结构与算法分析’
只谈数据结构 , 当然是可以,我们可 以在很短的时间就把几种重要的数据结构介绍完。听完后,很可能你没什么感觉,不 知道这些数据结构有何用处。 但如果我们再把相应的算法也拿来讲一讲,你就会发 现,甚至开始感慨
在《数据结构》课程中,就算谈到算法,也是为了帮助理解好数据结构,并 不会详细谈及算法的方方面面。
2.3两种算法的比较 19
高斯在上小学的一天,老师要求每个学生都计算1+2+…+100的结果,谁先算出来谁先回家……
int i , sum = 0, n ; 100;
for (i = 1; i < = n; i++) {
sum = sum + í ;
}
printf ("%d", sum) ;
int i, sum = 0, n = 100;
sum = (1 + n) * n / 2;
printf ( "%d", sum);
前面的累加程序显然计算机要循环一千、 一万、一亿次的加法运算。而高斯的方法只需要在瞬间之内完成。
2.4算法定义 20
现实世界中的算法千变万化,没有通用算法可以解决所有问题。甚至一个小问题,某个解决此类问题很优秀的算法却未必就适合它。
算法是解决特定问题求解步骤的描述,在计算机中表现为指令的有限序列,并且每条指令表示一个或多个操作
指令能被人或机器等计算装置执行。它可以是计算机 指令,也可以是我们平时的语言文字。为了解决某个或某类问题,需要把指令表示成一定的操作序列,操作序列包括一 组操作,每一个操作都完成特定的功能,这就是算法了。
2.5算法的特性 21
算法具有五个基本特性: 输入、输出、 有穷性、确定性和可行性。
算法具有零个或多个输入
算法至少有一个或多个输出
算法在执行有限的步骤后,自动结束而不会出现无限循环,并且每一个步骤在可接受的时间内完成
算法的每一步骤都具有确定的含义,不会出现二义性
算法的每一步都必须是可行的,也就是说,每一步都能够通过执行有限次数完成
2.5.1输入输出 21
2.5.2有穷性 21
2.5.3确定性 21
算法在一定条件 下,只有一条执行路径,相同的输入只能有唯一的输出结果@算法的每个步骤被精确定义而无歧义。
2.5.4可行性 21
2.6算法设计的要求 22
求100个人的高考成绩平均分与求全省所有考生的成绩平均分在占用时间和内存存储上有非常大的差异,我们自然追求高效率和低存储的算法来解决问题。
这可能让那些常年只做有标准答案题目的同学失望了, 他们多么希望存在 标准答案 , 只有一个是正确的,把它背下来,需要的时候套用就可以了。不过话说回 来, 尽管算法不唯一, 相对好的算法还是存在的。掌握好的算法,对我们解决问题很 有帮助 , 否则前人的智慧我们不能利用,就都得自己从头研究了。 那么什么才叫好的算法呢?
正确性、可读性、健壮性、时间效率高和存储量低
好的算法,应该具有正确性、 可读性、健壮性、 高效率和低存储量的特征。
2.6.1正确性 22
正确性:算法的正确性是指算法至少应该具有输入、输出和加工处理无歧义性、能正确反映问题的需求、能够得到问题的正确答案
正确性大体分为以下四个层次:
算法程序没有语法错误
算法程序对于合法的输入数据能够产生满足要求的输出结果
算法程序对于非法的输入数据能够产生满足规格说明的结果(一般情况下,将此作为判断一个算法是否正确的标准)
算法程序对于精心选择的,甚至刁难的测试数据都有满足要求的输出结果
证明一个复杂算法在所4寄层次上都是正确的,代价非常昂贵。所以一般情况下, 我们把层次 3 作为一个算法是否正确的标准。
2.6.2可读性 23
可读性:算法设计的另一个目的是为了便于阅读、理解和交流
可读性高有助于人们理解算法,晦涩难愤的算法往往隐含错误,不易被发现, 并 且难于调试和修改。
我们写代码的目的,一方面是为了让计算机执行,但还有一个重要的目的是为了 便于他人阅读, 让人理解和交流, 自 己将来也可能阅读,如果可读性不好,时间长了 自己都不知道写了些什么。
2.6.3健壮性 23
健壮性:当输入数据不合法时,算法也能做出相关处理,而不是产生异常或莫名其妙的结果
2.6.4时间效率高和存储量低 23
设计算法应该尽量满足时间效率高和存储量低的需求
时间效率指的是算法的执行时间 , 对于同一个问题,如果有多个算法能够解决, 执行时间短的算法效率高,执行时间长的效率低。
存储量需求指的是算法在执行过程中需要的最大存储空间, 主要指算法程序运行时所占用的内存或外部硬盘存储空间。
最好用最少的存储空间, 花最少的时间,办成同样的事就是好的算法。
2.7算法效率的度量方法 24
随着n值越来越大,它们在时间效率上的差异也就越来越大。好比有些人每天都在学习,而另一些人,打打游戏、睡睡大觉,毕业后前者名企争着要,后者求职处处无门。
我们通过对算法的数据测试,利用计算机的计时功能,来计算不同算法的效率是高还是低。
2.7.1事后统计方法 24
这种方法主要是通过设计好的测试程序和数据,利用计算机计时器对不同算法编制的程序的运行时间进行比较,从而确定算法效率的高低
缺陷:
必须依据算法事先编制好程序,这通常需要花费大量的时间和精力。
时间的比较依赖计算机硬件和软件等环境因素,有时会掩盖算法本身的优劣。
算法的测试数据设计困难,并且程序的运行时间往往还与测试数据的规模有很大关系,效率高的算法在小的测试数据面前往往得不到体现。
缺陷较大,不予采纳
2.7.2事前分析估算方法 25
在计算机程序编制前,依据统计方法对算法进行估算
经过分析, 我们发现, 一个用高级程序语言编写的程序在计算机上运行时所消耗的时间取决于下列因素:
- 算法采用的策略、 方法。
- 编译产生的代码质量。
- 问题的输入规模。
- 机器执行指令的速度。
第 1 条当然是算法好坏的根本,第 2 条要由软件来支持, 第 4 条要看硬件性能。 也就是说, 抛开这些与计算机硬件、软件有关的因素,一个程序的运行时间,依赖于算法的好坏和问题的输入规模。 所谓问题输入规模是指输入量的多少。
一个程序的运行时间,依赖于算法的好坏和问题的输入规模

显然,第一种算法,执行了 1+ (n+1) +0+1 次=2n+3 次,而第二种算法,是 1+1+1=3 次。
事实上两个算法的第一条和最后一条语句是一样的,所以我们关注的代 码其实是中间的那部分,我们把循环看作一个整体, 忽略头尾循环判断的开销, 那么 这两个算法其实就是 n 次与 1 次的差距。算法好坏显而易见。

这个例子中, i 从 1 到 100 ,每次都要让 j 循环 100 次,而当中的 x++和 sum = sum + x; 其实就是 1+2+3+…+10000 ,也就是 100^2 次,所以这个算法当中,循环部 分的代码整体需要执行 n^2 (忽略循环体头尾的开销)次。显然这个算法的执行次数对 于同样的输入规模 n = 100, 要多于前面两种算法,这个算法的执行时间随着 n 的增 加也将远远多于前面两个。
此时你会看到,测定运行时间最可靠的方法就是计算对运行时间有消耗的基本操作的执行次数, 运行时间与这个计数成正比。
我们不关心编写程序所用的程序设计语言是什么,也不关心这些程序将跑在什么 样的计算机中,我们只关心官所实现的算法。这样,不计那些循环索引的递增和循环终止条件、 变童声明、打印结果等操作, 最终,在分析程序的运行时间时,最重要的是把程序看成是强立于程序设计语言的算法或一系列步骤。
在分析程序的运行时间时,最重要的是把程序看成是独立于程序设计语言的算法或一系列步骤
可以从问题描述中得到启示,同样问题的输入规模是 n,求和算法的第一种,求 1+2+…+n 需要一段代码运行 n 次。那么这个问题的输入规模使得操作数量是 f (n) = n,显然运行 100 次的同一段代码规模是运算 10 的 10 倍。而第二种,无论 n 为 多少,运行次数都为 1,即 f (n) =1; 第三种,运算 100 次是运算 10 次的 100 倍。因为它是 f (n) =n^2。
我们在分析一个算法的运行时间时,重要的是把基本操作的数量与输入规模关联起来, 基本操作的数量必须表示成输入规模的函数:
我们可以这样认为,随着 n 值的越来越大,它们在时间效率上的差异也就越来越 大。
2.8函数的渐近增长 27
可以忽略加法常数
我们现在来判断一下,两个算法 A 和 B 哪个更好。 假设两个算法的输入规模都是 n,算法 A 要做 2n + 3 次操作,你可以理解为先有一个 n 次的循环,执行完成后,再 有一于n 次循环,最后有三次赋值或运算,共 2n + 3 次操作。 算法 B 要做 3n + 1 次 操作。 你觉得它们谁更快呢?
准确说来,答案是不一定的:

当 n = 1 时,算法 A 效率不如算法 B (次数比算法 B 要多一次)。 而当 n = 2 时, 两者效率相同 i 当 n>2 时,算法 A 就开始优于算法 B 了,随着 n 的增加,算法 A 比算法 B 越来越好了: (执行的次数比B要少)。于是我们可以得出结论,算法 A 总体上 要好过算法 B。
此时我们给出这样的定义,输入规模 n 在没有限制的情况下,只要超过一个数值 N ,这个函数就总是大于另一个函数,我的称函数是渐近增长的。
函数的渐近增长:给定两个函数f(n)和g(n),如果存在一个整数N,使得对于所有的n > N,f(n)总是比g(n)大,那么,我们说f(n)的增长渐近快于g(n)
从中我们发现,随着 n 的增大,后面的 +3 还是 +1 其实是不影响最终的算法变化 的,例如算法 A’ 与算法 B’ ,所以, 我们可以忽略这些加法常数。 后面的例子,这样的常数被忽略的意义可能会更加明显。
与最高项相乘的常数并不重要
算法 C 是 4n+8 ,算法 D 是 2n2 + 1
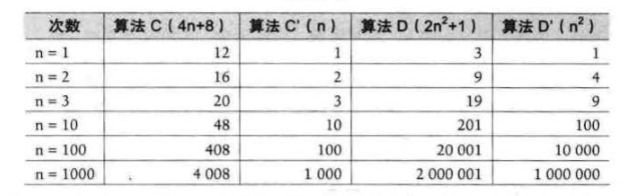
当 n<=3 的时候,算法 C 要差于算法 o (因为算法 C 次数比较多) ,但当 n > 3 后,算法 C 的优势就越来越优于算法 了,到后来更是远远胜过。而当后面的常数去 掉后,我们发现其实结果没有发生改变。 甚至我们再观察发现, 哪怕去掉与 n 相乘的 常数,这样的结果也没发生改变,算法 c’的次数随着 n 的增长,还是远小于算法D’ 。 也就是说, 与最高次项相乘的常数并不重要。
最高项的指数大的增加越快
算法 E 是 2n2 + 3n + 1,算法 F 是 2n3 + 3n + 1

当 n=l 的时候, 算法 E 与算法 F 结果相同,但当 n>l 后, 算法 E 的优势就要开 始优于算法 F,随着 n 的增大,差异非常明显。通过观察发现, 最高次项的指数大的,函数随着 n 的增长,结果也会变得增长特别快。
函数中的常数和其他次要项常常可以忽略,而更应该关注主项(最高阶项) 的阶数
算法 G 是 2n2,算法 H 是 3n + 1, 算法 1 是 2n2 + 3n + 1
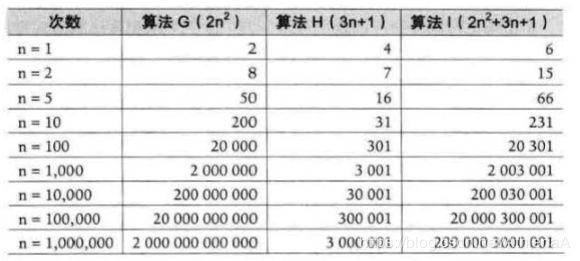
这组数据应该就看得很清楚。 当 n 的值越来越大时,你会发现, 3n+l 已经没法和 2旧 的结果相比较, 最终几乎可以忽略不计。也就是说, 随着 n 值变得非常大以后, 算法 G 其实已经很趋近于算法 l。于是我们可以得到这样一个结论, 判断…个算法的 效率时,函数中的常数和其他次要项常常可以忽略,而更应该关注主项(最高阶项) 的阶数。
判断一个算法好不好,我们只通过少量的数据是不能做出准确判断的。根据刚才 的几个样例 , 我们发现,如果我们可以对比这几个算法的关键执行次数函数的渐近增 长性,基本就可以分析出:某个算法,随着 n 的增大,宫会越来越优于另一算法,或 者越来越羞于另一算法。这其实就是事前估算方法的理论依据, 通过算法时间复杂度 来估算算法时间效率。
2.9算法时间复杂度 29
理解大o推导不算难,难的其实是对数列的一些相关运算,这考察的更多的是数学知识和能力。
2.9.1算法时间复杂度定义 29
在进行算法分析时,语句总的执行次数T(n)是关于问题规模n的函数,进而分析T(n)随n的变化情况并确定T(n)的数量级。
算法的时间复杂度,也就是算法的时间量度,记作:T(n)=O(f(n))。它表示随问题规模n的增大,算法执行时间的增长率和f(n)的增长率相同,称作算法的渐近时间复杂度,简称为时间复杂度,其中f(n)是问题规模n的某个函数
这样用大写 O()来体现算法时间复杂度的记法,我们称之为大O记法。
一般情况下,随着 n 的增大, T(n)增长最慢的算法为最优算法。
显然,由此算法时间复杂度的定义可知,我们的三个求和算法的时间复杂度分别 为 O(1) O(n) O(n2)。我们分别给官们取了非官方的名称,O(1)叫常数阶、 O(n)叫线性阶、 O(n2)叫平方阶,当然,还有其他的一些阶,我们之后会介绍。
2.9.2推导大o阶方法 30
推导大 O 阶:
1.用常数 1 取代运行时间中的所有加法常数。
2.在修改后的运行次数函数中,只保留最高阶项。
3.如果最高阶项存在且不是 1 ,则去除与这个项相乘的常数。
得到的结果就是大 O 阶。
2.9.3常数阶 30
不管n为多少,执行的次数都是恒定的,不会随着n的变大而发生变化,其时间复杂度为O(1)
这个算法的运行次数函数是 f (n) =30 根据我们推导大 0 阶的方法,第一步就是 把常数项 3 改为 1。在保留最高阶项时发现,它根本没有最高阶项,所以这个算法的时间复杂度为O(1)。
这种与问 题的大小无关 (n 的多少) ,执行时间恒定的算法,我们称之为具有 0(1)的时间复杂 度,又叫常数阶。
注意: 不管这个常数是多少,我们都记作 O(1),而不能是 O(3)、 O(12)等其他任 何数字,这是初学者常常犯的错误。
对于分支结构而言,无论是真,还是假,执行的次数都是恒定的,不会随着 n 的变大而发生变化,所以单纯的分支结构(不包含在循环结构中) ,其时间复杂度也是O(1)。
2.9.4线性阶 31
循环结构中的代码需要执行n次,其时间复杂度为O(n)
要确定某个算法的阶次,我们常常需要确定某个 特定语句或某个语句集运行的次数。因此,我们要分析算法的复杂度,关键就是要分 析循环结构的运行情况。
下面这段代码,它的循环的时间复杂度为 O(n) , 因为循环体中的代码须要执行 n次。
for(i = 0; i < n; i++){
//时间复杂度为O(1)的程序步骤序列
}
2.9.5对数阶 32
有多少个2相乘后大于n,则会退出循环
int count = 1;
while(count < n){
count = count * 2;
}
2x=n
由于每次 count 乘以 2 之后,就距离 n 更近了一分。 也就是说,有多少个 2 相乘 后大于 n ,则会退出循环。 由 2x=n得到 x=log2n。 所以这个循环的时间复杂度为 o( logn)。
2.9.6平方阶 32
两层循环嵌套
int i,j;
for(i = 0; i < n; j++){
for(j = i; j < n; j++){
//时间复杂度为O(1)的程序步骤序列
}
}
而对于外层的循环,不过是内部这个时间复杂度为 O(n)的语旬,再循环 n 次。 所 以这段代码的时间复杂度为 O(n2).
如果外循环的循环次数改为了时间复杂度就变为 O(mXn)。
所以我们可以总结得出,循环的时间复杂度等于循环体的复杂度乘以该循环运行的次数。

从这个例子,我们也可以得到一个经验,其实理解大 0 推导不算难,难的是对数 列的一些相关运算,这更多的是考察你的数学知识和能力,所以想考研的朋友,要想 在求算法时间复杂度这里不失分,可能需要强化你的数学,特别是数列方面的知识和 解题能力。
对于方法调用的时间复杂度又如何分析


函数体是打印这个参数。 其实这很好理解, funcöon 函数的时间复杂度是 0(1)。 所以整体的时间复杂度为 O(n).

事实上,这和刚才举的例子是一样的,只不过把嵌在内循环放到了函数中,所以 最终的时间复杂度为 0(n2)。
2.10常见的时间复杂度 35
有些时候,告诉你某些东西不可以去尝试,也是一种知识的传递。总不能非要去被毒蛇咬一口才知道蛇不可以去招惹吧。

2.11最坏情况与平均情况 35
我们查找一个有 n 个随机数字数组中的某个数字, 最好的 情况是第一个数字就是,那么算法的时间复杂度为 0(1) ,但也有可能这个数字就在最 后一个位置上待着,那么算法的时间复杂度就是 O(叶,这是最坏的一种情况了。
最坏情况运行时间是一种保证,那就是运行时间将不会再坏了。 在应用中,这是 一种最重要的需求, 通常, 除非特别指定, 我们提到的运行时间都是最坏情况的运行时间。
而平均运行时间也就是从概率的角度看 , 这个数字在每一个位置的可能性是相同的,所以平均的查找时间为 n/2 次后发现这个目标元素。
平均运行时闯是所有情况中最有意义的,因为它是期望的运行时间。也就是说, 我们运行一段程序代码时,是希望看到平均运行时间的。可现实中 ,平均运行时间很 难通过分析得到,一般都是通过运行一定数量的实验数据后估算出来的。
对算法的分析,一种方法是计算所有情况的平均值,这种时间复杂度的计算方法 称为平均时间复杂度。 另一种方法是计算最坏情况下的时间复杂度,这种方法称为最 坏时间复杂度。 一般在没有特殊说明的情况下,都是指最坏时间复杂度。
2.12算法空间复杂度 36
事先建立一个有2050大的数组,然后把所有年份按下标数字对应,如果是闰年,此数组项的值就是1,如果不是就是0。这样,所谓的判断某一年是否是闰年就变成了查找这个数组的某一项的值是多少的问题。

算法的空间复杂度通过计算算法所需的存储空间实现,算法空间复杂度的计算公式记作:S(n)=O(f(n)),其中,n为问题的规模,f(n)为语句关于n所占存储空间的函数
一般情况下, 一个程序在机器上执行时,除了需要存储程序本身的指令、常数、 变量和输入数据外,还需要存储对数据操作的存储单元,若输入数据所占空间只取决于问题本身,和算法无关,这样只需要分析该算法在实现时所需的辅助单元即可。若算法执行时所帘的辅助空间相对于输入数据量而言是个常数,则称此算法为原地工作,空间复杂度为 0(1)。
当不用限定词地使用”复杂度”时,通常都是指时间复杂度
2.13总结回顾 37
我们这一章主要谈了算法的一些基本概念。谈到了数据结构与算法的关系是相互 依赖不可分割的。
算法的定义:算法是解决特定问题求解步骤的描述,在计算机中为指令的有限序 列,并且每条指令表示一个或多个操作。
算法的特性: 有穷性、确定性、可行性、输入、输出。
算法的设计的要求: 正确性、可读性、健壮性、 高效率和低存储量需求。
算法特性与算法设计容易混,需要对比记忆。
算法的度量方法: 事后统计方法(不科学、不准确)、 事前分析估算方法。
在讲解如何用事前分析估算方法之前,我们先给出了函数潮近增长的定义。
函数的渐近增长:给定两个函数 f(n)和 g(吟,如果存在一个整数 N" 使得对于所 有的 n > N, f(n)总是比 g(n)大,那么,我们说 f(n)的增长渐近快于 g(n)。 于是我们可 以得出一个结论,判断一个算法好不好,我们只通过少量的数据是不能做出准确判断 的 ,如果我们可以对比算法的关键执行次数函数的渐近增长性,基本就可以分析出 : 某个算法,随着 n 的变大,它会越来越优于另一算法,或者越来越差于另一算法。
然后给出了算法时间复杂度的定义和推导大 0 阶的步骤。
推导大 O 阶:
• 用常数 1 取代运行时间中的所有加法常数。
• 在修改后的运行次数函数中,只保留最高阶项。
• 如果最高阶项存在且不是 1 ,则去除与这个项相乘的常数。
得到的结果就是大 O 阶。
通过这个步骤,我们可以在得到算法的运行次数表达式后,很快得到宫的时间复 杂度,即大O阶。同时我也提醒了大家,其实推导大 O阶很容易,但如何得到运行次 数的表达式却是需要数学功底的。
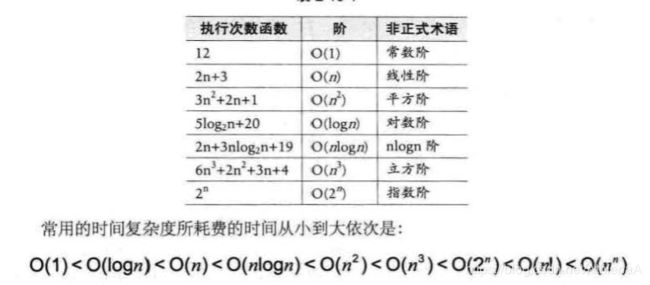
接着我们给出了常见的时间复杂度所耗时阔的大小排列:
0(1) < O(logn) < O(n) < O(nlogn) < 0(n2 ) < 0(n3 ) < 0(2") < O(n!) < O(nn)
最后,我们给出了关于算法最坏情况和平均情况的概念,以及空间复杂度的概念。
2.14结尾语 38
愚公移山固然可敬,但发明炸药和推土机,可能更加实在和聪明。
一台老式 CPU 的计算机运行 O(n)的程序和一台速度提高 100 倍新式 CPU 运行 。(n2)的程序。最终效率高的胜利方却是老式 CPU 的计算机,原因就在于算 法的优劣直接决定了程序运行的效率。
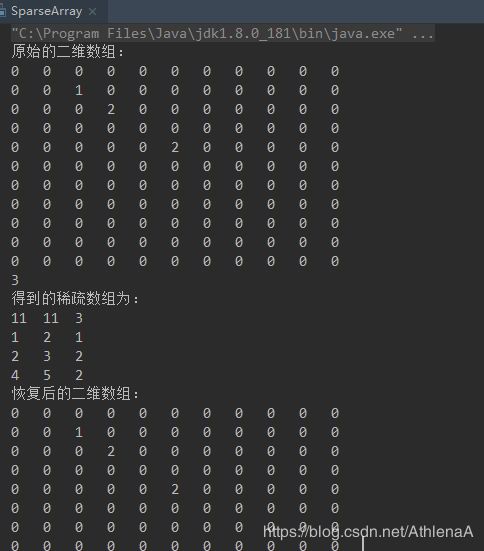
稀疏数组
稀疏sparsearray数组
编写的五子棋程序中,有存盘退出和续上盘的功能。

因为该二维数组的很多值是默认值0, 因此记录了很多没有意义的数据.->稀疏数组。
基本介绍
当一个数组中大部分元素为0,或者为同一个值的数组时,可以使用稀疏数组来保存该数组。
稀疏数组的处理方法是:
记录数组一共有几行几列,有多少个不同的值
把具有不同值的元素的行列及值记录在一个小规模的数组中,从而缩小程序的规模

应用实例
使用稀疏数组,来保留类似前面的二维数组(棋盘、地图等等)
把稀疏数组存盘,并且可以从新恢复原来的二维数组数
整体思路分析
代码实现


package com.zcr.sparsearray;
/**
* @author zcr
* @date 2019/7/4-21:42
*/
public class SparseArray {
public static void main(String[] args) {
//创建一个原始的二维数组11*11
//0表示没有棋子,1表示黑子,2表示蓝子
int chessArr1[][] = new int[11][11];
chessArr1[1][2] = 1;
chessArr1[2][3] = 2;
chessArr1[4][5] = 2;
//输出原始的二维数组
System.out.println("原始的二维数组:");
for (int[] row : chessArr1) {
for (int data : row) {
System.out.printf("%d\t",data);
}
System.out.println();
}
//将二维数组转化位稀疏数组
//1.先遍历二维数组得到非0数据的个数
int sum = 0;
for (int i = 0; i < chessArr1.length; i++) {
for (int j = 0; j < chessArr1[0].length; j++) {
if (chessArr1[i][j] != 0) {
sum++;
}
}
}
System.out.println(sum);
//2.创建对应的稀疏数组
int sparseArr[][] = new int[sum + 1][3];
//给稀疏数组赋值
sparseArr[0][0] = chessArr1.length;
sparseArr[0][1] = chessArr1[0].length;
sparseArr[0][2] = sum;
//3.遍历二维数组,将非0的值存放到稀疏数组中
int count = 0;//用于记录是第几个非0数据
for (int i = 0; i < chessArr1.length; i++) {
for (int j = 0; j < chessArr1[0].length; j++) {
if (chessArr1[i][j] != 0) {
count++;
sparseArr[count][0] = i;
sparseArr[count][1] = j;
sparseArr[count][2] = chessArr1[i][j];
}
}
}
//4.打印稀疏数组
System.out.println("得到的稀疏数组为:");
for (int i = 0; i < sparseArr.length; i++) {
System.out.printf("%d\t%d\t%d\t\n",sparseArr[i][0],sparseArr[i][1],sparseArr[i][2]);
}
//将稀疏数组恢复为原始二维数组
/**
* 1.先读取稀疏数组的第一行,根据第一行的数据,创建原始的二维数组
* 2.在读取稀疏数组后几行的数据,并赋给原始的二维数组即可
*/
int chessArr2[][] = new int[sparseArr[0][0]][sparseArr[0][1]];
for (int i = 1; i < sparseArr.length; i++) {
for (int j = 0; j < sparseArr[0].length; j++) {
chessArr2[sparseArr[i][0]][sparseArr[i][1]] = sparseArr[i][2];
}
}
System.out.println("恢复后的二维数组:");
for (int[] row : chessArr2) {
for (int data : row) {
System.out.printf("%d\t",data);
}
System.out.println();
}
}
}
课后练习
要求:
在前面的基础上,将稀疏数组保存到磁盘上,比如 map.data
恢复原来的数组时,读取map.data 进行恢复