反转链表这题真的是面试非常喜欢考的了,这题看起来简单,但是能用两种方法一遍 bug free 也是不容易的,面试的时候可以筛下来一大批人,无论是对 junior 还是 senior 面试都很爱考。
今天齐姐就带你梳理清楚思路,思路清楚了才能写码如有神。
题目
这是从力扣中文站上截下来的,但是这个输出不太形象。
对链表的反转,并不是要把它实际翻个个,只是动一动 next 指针就好了。
什么意思呢?
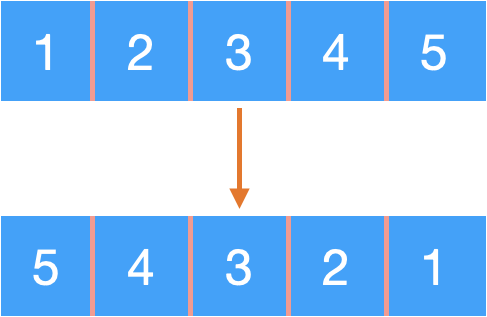
我们先看对数组进行反转。
数组是一个物理上连续存储的数据结构,反转之后原来放 1 的位置就变成了放 5.
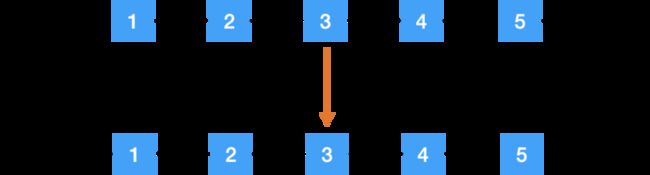
但是链表并不是,因为链表在物理上是不连续的,它的每个单元 ListNode 是通过 next 指针连接在一起的,而每个 ListNode 之间在内存里并不一定是挨着的。
所以反转链表,就不是非要把 1 的位置放 5,因为它们想在哪在哪。
那么怎么保证这个顺序呢?
- 就是 next 指针。
沿着 next 指针的方向走下去,就是链表的顺序。这也就保证了,只要我们拿到了头节点,就掌控了整个 LinkedList.
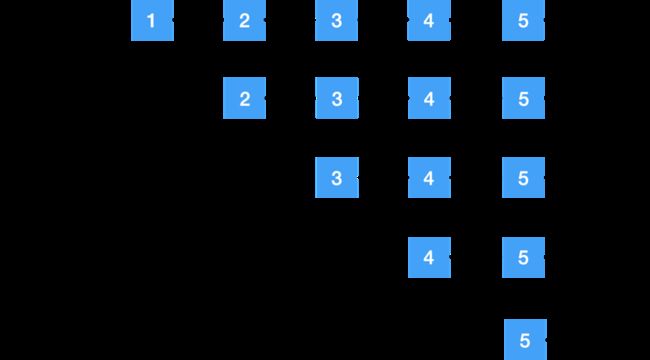
那么题目中的例子,形象点是这个样子滴:
也就是元素自己不用动,只需要动动小指针,就是反转了。
递归解法
递归的三步骤大家还记得吗?
Base case + 拆解 + 组合
不记得的赶紧在公众号内回复「递归」二字,获取递归的入门篇详解。
那么我们来看这个题的:
base case:
当只有一个 node,或者没有 node 了呗,也就是
if(node == null || node.next == null) {
return node;
}其实呢,只剩一个 node 的时候严格来讲并不是 base case,而是 corner case,
因为它本可以再 break down 到 node == null 的,但因为后面有对 node.next 的 dereference 操作,所以不能省略。
拆解:
递归的拆解就是把大问题,分解成小一点点的问题,直到 base case 可以返回,进行第三步的组合。
那么这里就是
组合:
组合的意思是,假设我们能够拿到小问题的解,那么用小问题的解去构造大问题的解。
那么这个问题里如何构造呢?
这里很明显,在 2 后面接上 1 就行了,但是怎么拿到 2 呢?
别忘了,原问题里,此时还有 1 指向 2 呢~
也就是 node1.next = node2,
然后把 2 指向 1:node2.next = node1
合起来就是:node1.next.next = node1
思路清楚就不绕,看着觉得绕的就是没想清楚哼~
代码
递归的代码写起来都很简洁:
class Solution {
public ListNode reverseList(ListNode head) {
if(head == null || head.next == null) {
return head;
}
ListNode newHead = reverseList(head.next);
head.next.next = head;
head.next = null;
return newHead;
}
}时间复杂度
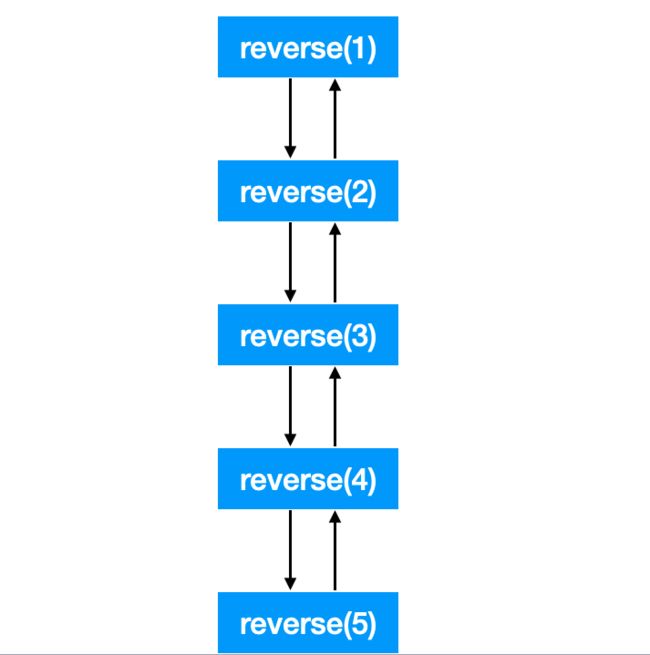
我们在「递归」这篇文章里说过,递归的时间复杂度分析方法就是把递归树画出来,每个节点的时间加起来就行了。
这个递归树是一个很简单的单项链表,每个节点上做的就是那三行代码,也就是「组合」做的事,即 O(1) 的时间,总共有 n 个节点,那么总的时间就是 O(n).
空间复杂度
那看递归树也很明显了,每一层也就用了点小变量,是 O(1),所以总的空间共是 O(n).
Iterative 解法
(谁能告诉我这个中文的专业说法。。
Iterative 的思路就是:
过一遍这个 Linked List,边过边把这个 node 的 next 指针指向前面那个 node,直到过完全部。
这样说太抽象,面试时也是,直接过例子。
那也就是把 1 的 next 指针翻过来指向 NULL;
把 2 的 next 指针翻过来指向 1;
把 3 的 next 指针翻过来指向 2;
...
所以我们还需要一个变量来记录当前 node 的前一个 node,不妨设为 prev.
同时呢,一旦我们把指针翻转过去,后面的那个 node 就丢了有木有!所以还需要有个额外的变量事先记录下后面的 node,设为 nxt,这样才不至于走丢~
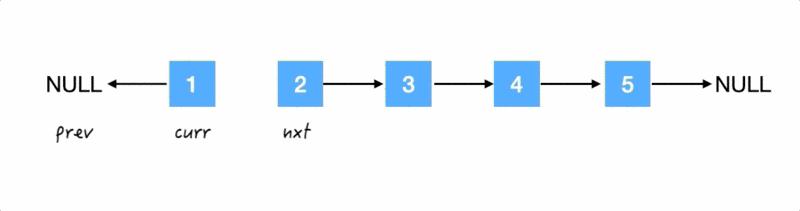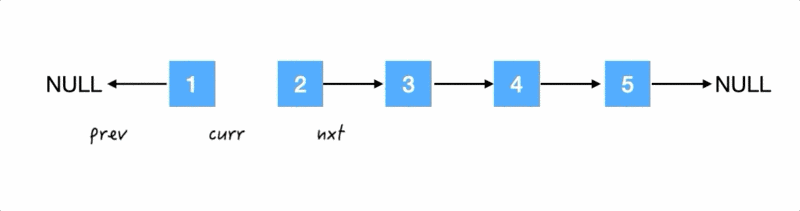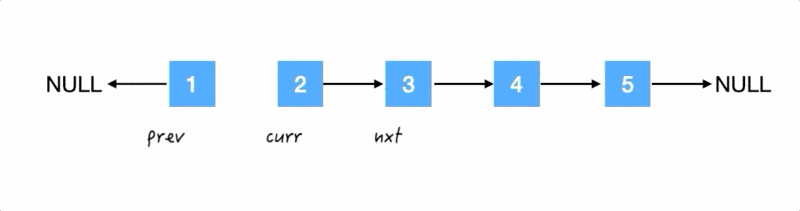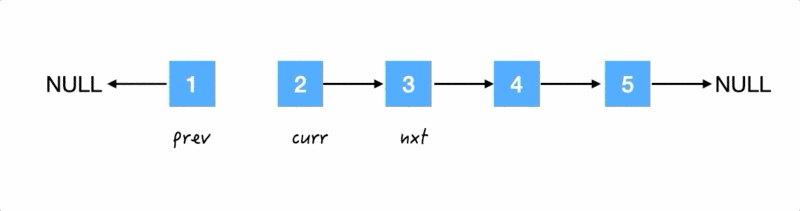
Step1.
翻转箭头:把 1 的 next 指针指向 NULL;
这样子,同时我们也明确了,prev 的初始化应该是 NULL.
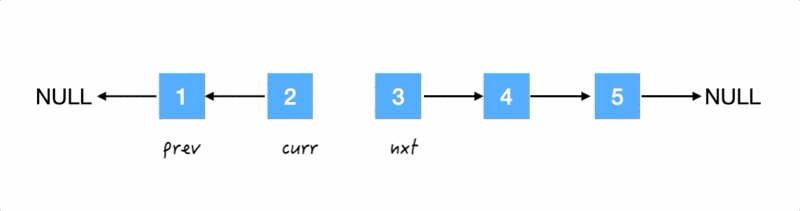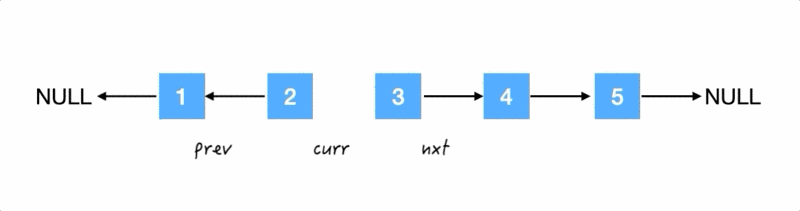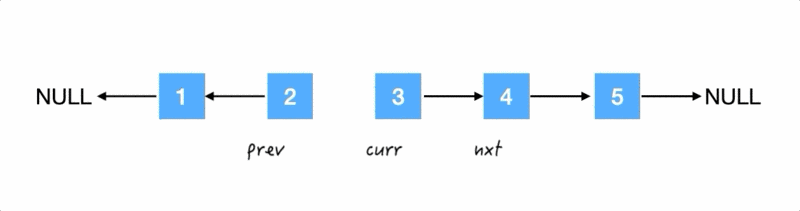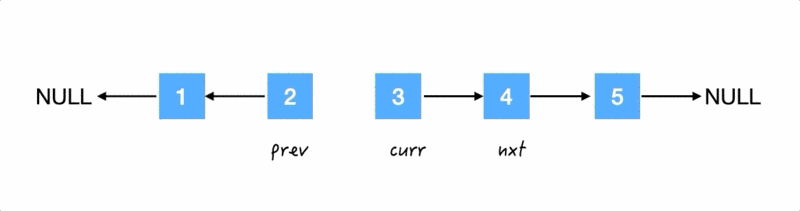
然后把这仨变量都移动到下一个位置:
Step2.
翻转箭头:把 2 的 next 指针指向 1,
然后三人行:
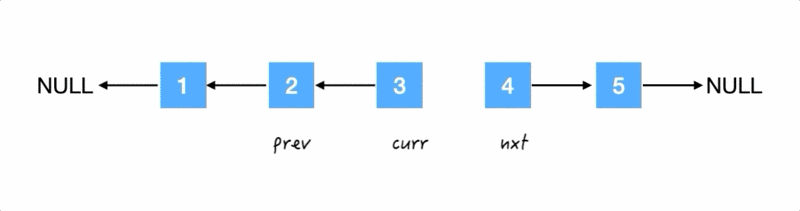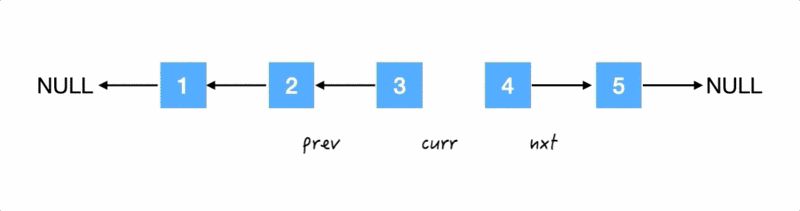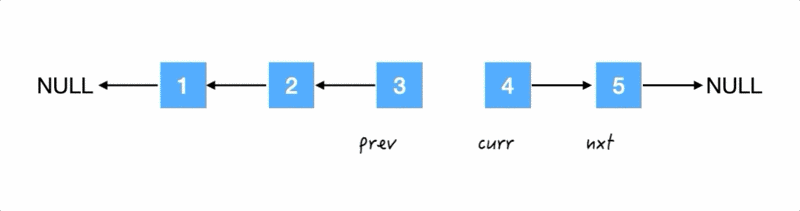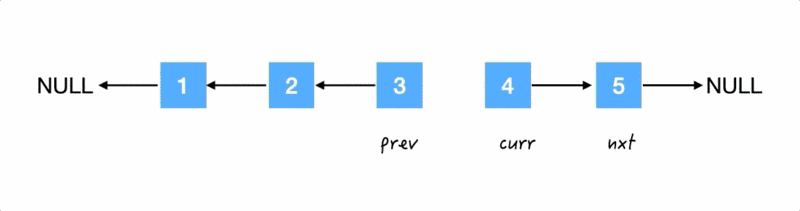
Step3.
翻转箭头:把 3 的 next 指针指向 2,
再齐步走:
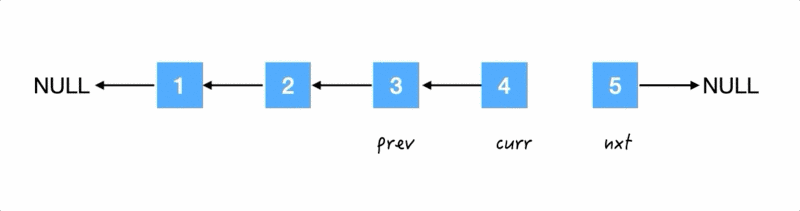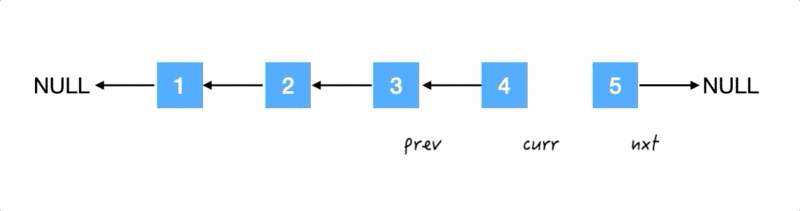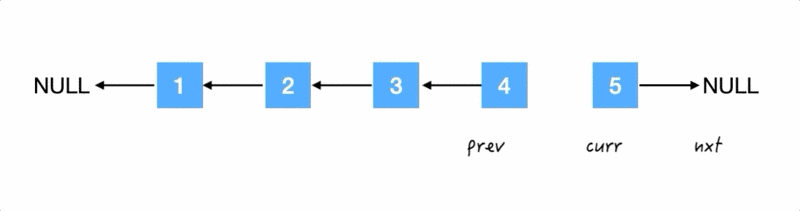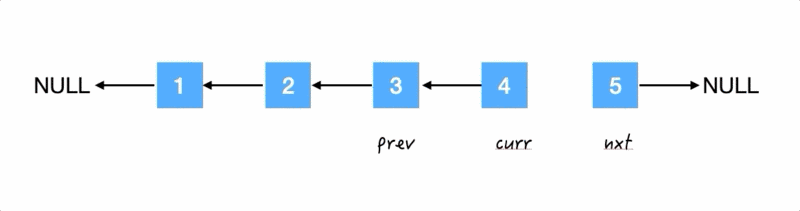
Step4.
再把 4 的反过来:
再往后走:
Step5.
再把 5 的 next 反过来:
但是因为我们的 while 循环包含了
「翻转箭头」+「三人行」
两个步骤,所以还需要走完最后一个三人行,变成:
很多同学搞不清楚这个 while 循环的结束条件,其实很简单,你就走个例子画画图嘛!
那结束条件就是 curr = null 的时候,
最后返回的是 prev.
好了,看代码吧:
class Solution {
public ListNode reverseList(ListNode head) {
ListNode prev = null;
ListNode curr = head;
while(curr != null) {
ListNode nxt = curr.next;
curr.next = prev; // 翻转箭头
prev = curr; //三人行
curr = nxt; //三人行
}
return prev;
}
}时间复杂度
这里的时间复杂度很明显了,就是过了一遍这个链表,所以是 O(n).
空间复杂度
空间是 O(1).