典型算法算法以及应用
目录
一、 评估你的复杂度
二、深度优先搜索
必须弄清楚的递归思想:
简单的深度搜索框架
深度搜索的优化:迭代加深(ID DFS)
深度搜索的优化: IDA*
*重叠子问题(记忆化搜索)
三、宽度优先搜索
宽度优先搜索框架:
分支定界:
A*
四、二分查找
查找有序数列中的某个值
二分查找算法分析
STL中的二分法查找:
二分答案(不只是查找值)
一、 评估你的复杂度
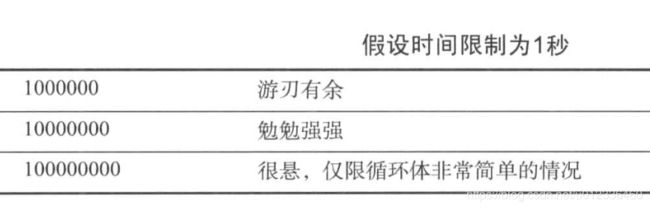
简单的判断算法是否能满足运行时间限制的要求
密切关注题中的给出的数据规模,选择相应的算法
样例:
输入:
3
10
1 3 5
输出:
Yes
解析: 4次抽取的结果为 1,1,3,4 和就是10
输入:
3
9
1 3 5
输出:
No
时间复杂度为O(n4)的枚举方法。 若n的条件限制为 1<=n <=1000 超时
穷举 多重循环形式的枚举
for(int a=0; a![]() 改进,时间复杂度O( n2log2n) 的 方法:预处理一下(排序)
改进,时间复杂度O( n2log2n) 的 方法:预处理一下(排序)
sort(k, k+n);
for(int a=0; a改进,再改进:搜索预处理(空间换时间)
#include
using namespace std;
const int MAX_N=51;
int k[MAX_N];
int kk[MAX_N * MAX_N];
int main()
{
int n, m; //n个数。取四次, 要求和为m;
cin >>n >>m;
for(int i=0;i> k[i];
for(int i=0;i
从本质来说:深度搜索,宽度搜索本质上就是穷举。
二、深度优先搜索
必须弄清楚的递归思想:
在一个子程序(过程或函数)的定义中又直接或间接地调用该子程序本身,称为递归。递归是一种非常有用的程序设计方法。用递归算法编写的程序结构清晰,具有很好的可读性。
递归算法的基本思想是:把规模大的、较难解决的问题变成规模较小的、易解决的同一问题。规模较小的问题又变成规模更小的问题,并且小到一定程度可以直接得出它的解,从而得到原来问题的解。
利用递归算法解题,首先要对问题的以下三个方面进行分析:
一、决定问题规模的参数。需要用递归算法解决的问题,其规模通常都是比较大的,在问题中决定规模大小(或问题复杂程度)的量有哪些?把它们找出来。
二、问题的边界条件及边界值。在什么情况下可以直接得出问题的解?这就是问题的边界条件及边界值。
三、解决问题的通式。把规模大的、较难解决的问题变成规模较小、易解决的同一问题,需要通过哪些步骤或等式来实现?这是解决递归问题的难点。把这些步骤或等式确定下来。
把以上三个方面分析好之后,就可以在子程序中定义递归调用。其一般格式为:
int dream(int n){
if ( n==0 ) return 1
else return dream( n -1)
}
if 边界条件1成立
赋予边界值1
else
调用解决问题的通式简单的深度搜索框架
深度搜索的算法框架:(牢记)
例题:
部分和的问题:
样例
输入:
4
1 2 4 7
13
输出
Yes
输入:
4
1 2 4 7
15
输出:
No
有些题目要自己构造搜索树。
#include
using namespace std;
const int MAX_N = 21;
int n;
int k;
int a[MAX_N];
bool dfs(int deep , int sum){
if(sum==k) return true; //这里可以剪枝;
if( deep == n) {
return (sum == k);
}
if( dfs( deep+1 , sum + a[deep+1]) ) return true;
if( dfs( deep+1, sum)) return true;
return false;
}
int main()
{
cin >>n;
for(int i=1;i<=n;i++)
cin >> a[i];
cin >>k;
if( dfs(0,0) ) cout <<"Yes";
else cout <<"No";
return 0;
}
版本二:将sum作为全局变量(要注意恢复现场)
//版本一 将sum作为全局变量
#include
using namespace std;
const int MAX_N = 21;
int n;
int k;
int a[MAX_N];
int sum=0;
bool dfs(int deep){
if(sum==k) return true; //这里可以剪枝;
if( deep == n) {
return (sum == k);
}
sum = sum + a[deep+1];
if( dfs( deep+1 ) ) return true;
sum = sum- a[deep+1];
sum = sum + 0;
if( dfs( deep+1) ) return true;
sum = sum - 0 ;
return false;
}
int main()
{ cin >>n;
for(int i=1;i<=n;i++)
cin >> a[i];
cin >>k;
if( dfs(0) ) cout <<"Yes";
else cout <<"No";
return 0;
}
深度搜索的优化:迭代加深(ID DFS)
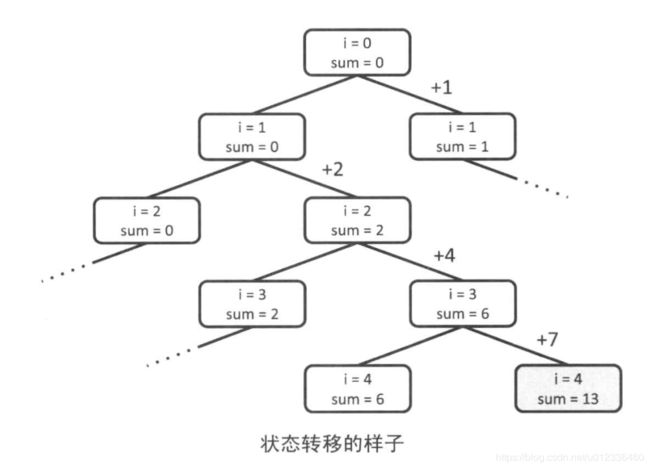
ID DFS是什么:在DFS的搜索里面,可能会面临一个答案的层数很低,但是DFS搜到了另为一个层数很深的分支里面导致时间很慢,但是又卡BFS的空间,这个时候,可以限制DFS的搜索层数,一次又一次放宽搜索的层数,知道搜索到答案就退出,时间可观,结合了BFS和DFS的优点于一身。
迭代加深搜索,就是在深度无上限的情况下,先预估一个深度(尽量小)进行搜索,如果没有找到解,再逐步放大深度搜索。这种方法虽然会导致重复的遍历 某些结点,但是由于搜索的复杂度是呈指数级别增加的,所以对于下一层搜索,前面的工作可以忽略不计;
其实写一下dfs然后不停的加大最大的搜索深度。
以下是迭代加深的简洁的框架:
bool bk;
void dfs(int limit,int depth)
{
if(...)
{
bk=true;
return ;
}
if(depth == limit )return ;
for(...) dfs(limit,depth +1);
}
for(int lim=1; ; lim++)
{
dfs( lim,0 );
if(bk==true) return 0;
}
例题:埃及分数问题:
https://www.rqnoj.cn/problem/240
在古埃及,人们使用单位分数的和(形如1/a的分数, a是自然数)表示一切有理数。 如:2/3=1/2+1/6,但不允许2/3=1/3+1/3,因为加数中有相同的。
对于一个分数a/b,表示方法有很多种,但是哪种最好呢? 首先,加数少的比加数多的好,其次,加数个数相同的,最小的分数越大越好。 如:
19/45=1/3 + 1/12 + 1/180
19/45=1/3 + 1/15 + 1/45
19/45=1/3 + 1/18 + 1/30
19/45=1/4 + 1/6 + 1/180
19/45=1/5 + 1/6 + 1/18
最好的是最后一种,因为 1/18 比1/180,1/45,1/30,1/180 都大。 给出 a , b ( 0 < a < b < 1000 ) , 计算出 a/b 的最好的表达方式。
---------------------
这道题显然我们既不能用DFS深搜(因为分数的个数不限),也不能用BFS广搜(因为分母也是无限的),但由题意可知,我们要做到的是最少的分数个数,并且最大的分母尽量小,我们可以考虑一种新的搜索——迭代加深。可以认为它结合了DFS与BFS,在限定的层数内深搜
于是这道题我们便找到了正确的搜索方法:先不断递增分数的个数,第一次找到的一定是个数最小的解,然后处理最优性问题,首先我们不能在找到一组解之后就直接return ,这样只满足了第一个目标,正确做法应该是返回上一层继续递归。那么什么情况下才会break呢?我们假设当前还可以枚举 d 个分数 , 当前剩余的分数是 a/b , 枚举的分母为 i , 如果d/i<=a/b,我们就可以 break 掉了,这是因为如果后面都是 1/i 也只能小于等于目标,那么肯定不存在解了,因为分母必须严格递增。
#include
#define N 100001
using namespace std;
typedef long long LL;
LL best,ans[N],flag,way[N];
void dfs(int limit, LL x , LL y , LL dep)
{
LL l1,l2,xx,yy,i,j;
l1 = max(way[dep - 1] + 1 , y / x); //寻找当前层数分母的最小值
l2 = min(y * (limt -dep + 1) / x , best - 1);//寻找当前层数分母的最大值
if(dep == limt) return;
for(i = l1 ; i <= l2 ; i ++)
{
xx = x; yy = y; way[dep] = i; //
xx = xx * i - yy; //计算剩余的分子
if(x < 0) continue;
yy = yy * i; //计算剩余的分母
dfs(xx,yy,dep + 1);
if(i < best && xx == 0)
{
flag = 1 ; best = i;
for(j = 1 ; j <= limt ; j ++)ans[j] = way[j]; //更新答案
}
}
}
int main()
{
//freopen("lx.in","r",stdin);
LL a,b,
cin >> a >> b;
cout< 思路:对于可以用回溯法求解,但是解答树的深度没有明显上限的题目,可以考虑迭代加深。
深度搜索的优化: IDA*
以迭代加深搜索框架为基础,将原来简单的深度限制加强为: 当前深度 + 未来估算步数 > 深度限制,则立即从单签分枝回溯。
*重叠子问题(记忆化搜索)
备忘录可以记忆化,下次就可以直接调用之前搜索过的结果 ,考虑使用位运算,速度可以加快些.对于一些可以转移的状态之间的搜索,我们可以考虑Hash或者是状压下来,进行记忆化,那么对于以后再次搜到这个状态我们就可以直接调用了.
例题:滑雪:https://www.luogu.org/problemnew/show/P1434
例题:NOIP2001 数的计数
记忆化搜索中你很可能会用到的:Hash方法 与 状态压缩方法
状态压缩你会要用到的位操作
三、宽度优先搜索
flood fill: 就好像在这里泼了一瓶墨水,漫散开来
宽度优先搜索框架:
宽度优先搜索, 尽可能利用STL中的 Queue 。
例如: 网络爬虫在抓取网页的时候,会将链接指向的网页的所有URL加入队列功供后续处理。
例题:丢失的牛 https://www.luogu.org/problemnew/show/P1588
#include
#include
#include
#include
using namespace std;
struct per
{
int x,step;
per(int xx,int st)
{x=xx;step=st;}
};
queue q;//队列
bool vis[2000005];
int from,to;
bool in(int x)
{
return x<0 || x>(to<<1) || vis[x];
}//判断是否越界
int bfs()
{
memset(vis,0,sizeof(vis));
while(!q.empty())q.pop();
//记得清空数组与队列
if(from>=to)return from-to;
//特判,因为from==to时是0,也是from-to,就把两个放一起了
q.push(per(from,0));vis[from]=1;
while(!q.empty())
{
int xx=q.front().x,st=q.front().step;//获取头元素
if(xx==to)return st;
if(in(xx+1)==false) q.push(per(xx+1,st+1)),vis[xx+1]=1;
if(in(xx-1)==false) q.push(per(xx-1,st+1)),vis[xx-1]=1;
if(in(xx*2)==false) q.push(per(xx*2,st+1)),vis[xx*2]=1;//枚举每个点
q.pop();
}
return -999;
}
int main()
{
int t;
scanf("%d",&t);
while(t--)//多组答案
scanf("%d%d",&from,&to),printf("%d\n",bfs());
} 例如:分油问题,一个一进的瓶子装满油,另有一个七两盒一个三两的空瓶,在没有其他工具。只用这三个瓶子怎样精确地把一斤油分成两个半斤。
https://www.luogu.org/problemnew/solution/P1451
例题:求细胞数量 https://www.luogu.org/problemnew/show/P1451
#include
using namespace std;
struct P{
int x;
int y;
int dis;
P(int x,int y ,int dis){
this->x =x;
this->y=y;
this->dis=dis;
}
};
int N,M;
char yard[100][100];
int dx[]={0, 0 , 1, -1 };
int dy[]={1 , -1 , 0, 0 };
int sx,sy,gx,gy;
void bfs(){
queue Q;
Q.push( P(sx,sy,0) );
while( !Q.empty() ) {
P p=Q.front(); Q.pop();
for(int i=0;i<4;i++){
int newx = p.x + dx[i];
int newy = p.y + dy[i];
if( newx == gx && newy == gy ) {
cout << p.dis + 1;
return;
}
if( newx>=0 && newx0 && newy> N >> M ;
for(int i=0;i> t;
if( t=='S') { sx=i; sy=j;}
if( t=='G') { gx=i; gy=j;}
yard[i][j] = t;
}
}
bfs();
return 0;
}
深度优先于宽度搜索优先的区别与联系:
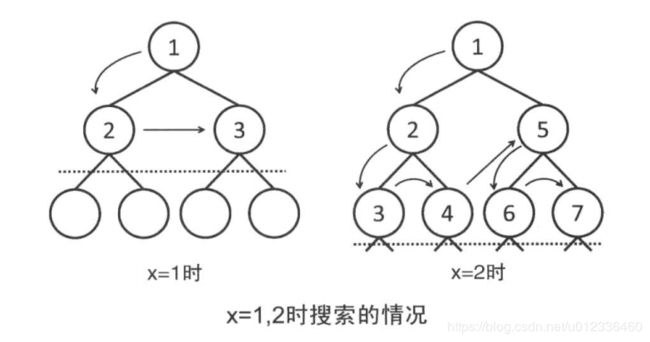
都会扩展每个节点的所有节点,而不同的是:在对于扩展节点的选取上, 深度搜索下一次扩展是本次扩展的子节点中的一个,而广度搜索是本次扩展的节点的兄弟节点。广度搜索一般只用于找最优解。深度搜索可以搜索出所有的解。
分支定界:
https://mp.csdn.net/postedit/83929560
分支定界实际上是A*算法的一种雏形,其对于每个扩展出来的节点给出一个预期值,如果这个预期值不如当前已经搜索出来的结果好的话,则将这个节点(包括其子节点)从解答树中删去,从而达到加快搜索速度的目的。
例如:某公司于乙城市的销售点急需一批成品,该公司成品生产基地在甲城市。甲城市与乙城市之间共有n 座城市,互相以公路连通。甲城市、乙城市以及其它各城市之间的公路连通情况及每段公路的长度由矩阵M1 给出。每段公路均由地方政府收取不同额度的养路费等费用,具体数额由矩阵M2 给出。 请给出在需付养路费总额不超过1500 的情况下,该公司货车运送其产品从甲城市到乙城市的最短运送路线。
A*
A*是对于bfs的优化,启发式搜索。(本质是一个带有估价函数的优先队列BFS)
这是我看到的做好的 A*算法课程: https://www.redblobgames.com/pathfinding/a-star/introduction.html
四、二分查找
查找有序数列中的某个值
设算法的输入实例中有序的关键字序列为
(05,13,19,21,37,56,64,75,80,88,92)
1 2 3 4 5 6 7 8 9 10 12
顺序查找:如果按顺序查找,分析一下查找成功的时间复杂度。查找数值21,你能模拟一下么?
二分查找算法分析
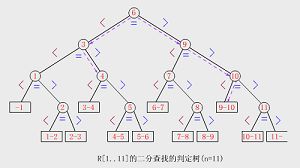
① 执行过程
二分查找过程可用二叉树来描述:把当前查找区间的中间位置上的结点作为根,左子表和右子表中的结点分别作为根的左子树和右子树。由此得到的二叉树,称为描述二分查找的判定树(Decision Tree)或比较树(Comparison Tree)。
② 二分查找的平均查找长度
设内部结点的总数为n=2h-1,则判定树是深度为h=lg(n+1)的满二叉树(深度h不计外部结点)。树中第k层上的结点个数为2k-1,查找它们所需的比较次数是k。因此在等概率假设下,二分查找成功时的平均查找长度为:
ASLbn≈lg(n+1)-1
二分查找在查找失败时所需比较的关键字个数不超过判定树的深度,在最坏情况下查找成功的比较次数也不超过判定树的深度。即为:
![]()
二分查找的最坏性能和平均性能相当接近。
代码:binary_research()
#include
using namespace std;
const int N =10;
int a[12]={0 ,5, 13,19, 21,37,56,64,75,80,88,92};
int my_research(int L, int R, int key){
int first = L, last = R-1;
while(first < last){
int middle = (first+last)/2;
if( a[middle]==key)
return middle;
else
if( a[middle] < key ) first = middle+1;
else last=middle-1;
}
return -1;
}
int main()
{
cout << my_research(1, 12,44);
return 0;
}
STL中的二分法查找:
(05,13,19,21,37,56,64,75,80,88,92)
1 2 3 4 5 6 7 8 9 10 12如果要查找有序数组里面的元素V, 然而数组里面有多个元素都是V。
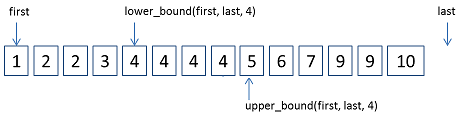
lower_bound : 算法返回一个非递减序列[ first, last )中的第一个大于等于值V的位置。当V存在时,返回出现的第一个位置。 若果不存在,则返回一个这样的下标: 在此处插入V,序列依然有序
#include
using namespace std;
const int N =10;
int a[12]={0 ,5, 13,21, 21,21,21,64,75,80,88,92};
int my_lower_bound(int L, int R, int key){
int first = L, last = R-1;
while(first < last){
int middle = (first+last)/2;
if( a[middle] >= key ) last = middle;
else first = middle+1;
//这里要注意,不能是middle 若果是middle,[middle, last] 可能与[fist, last]区间一样,将发生死循环
}
return first;
}
int main()
{
cout << my_research(1, 12,21);
return 0;
}
若 a[middle] ==key ,至少已经找到一个,然后左边可能还有, 因此区间变成 【first , middle】
若 a[middle] > key ,所找的位置,不可在后面。 若找不到,有可能是middle位置, 因此区间变成 【first , middle】
若 a[middle] < key ,所找的位置不可能是middle,也不可能在前面 因此区间变成 【middle+1, last】
upper_bound:算法返回一个非递减序列[ first, last )中第一个大于val的位置。当V存在时,返回出现的最后一个位置的下一个位置。若果不存在,则返回一个这样的下标: 在此处插入V,序列依然有序
如果想得到值等于V的完整区间呢? lower_bound 返回L位置, upper_bound返回R位置。 [ L, R ) ,若果L=R,区间为空。
#include
using namespace std;
const int N =10;
int a[12]={0 ,5, 13,21, 21,21,21,64,75,80,88,92};
int my_upper_bound(int L, int R, int key){
int first = L, last = R-1;
while(first < last){
int middle = (first+last)/2;
if( a[middle] <= key ) first = middle+1;
else last = middle;
}
return first;
}
int main()
{
cout << my_research(1, 12,21);
return 0;
}
实数区域上的二分
确定好精度 以 L + esp < R 为循环条件 ,一般需要保留2位小数时候,则取精度eps = le-4
while(L+ esp < R){
double mid = (L + R) /2
if ( ) R = middle else L = middle
}或者干脆采用循环固定次数的方法,也是不错的策略
for(int i=0;i<100;i++){
double middle = (L+R) /2;
if() L=middle; else R =middle
}二分答案(不只是查找值)
题目描述中若出现类似: “最大值最小”的含义,这个答案就具有单调性,可用二分答案法。
这个宏观的最优化问题,可以抽象为一个函数,其“定义域”是该问题的可行方案。
考虑“求某个条件C(x)的最小x” ,这个问题,对于任意满足C(x)的x,如果所有的x’ > x 也满足C(x’)的话,这个问题可以想像成一个特殊的单调函数,在s的一侧不合法,在s的另一侧不合法,我们就可以用二分法找到某得分界点。
例题:POJ 1905
热胀冷缩(expanding.in/out/pas/c/cpp) (POJ 1905)
我们知道,一般情况下,细金属棒加热后会膨胀变长。比如,某种长度为L的金属棒,当加热n度后,它的新长度为S = (1 + n * C) * L,其中C是热碰撞系数。
现在我们将此金属棒固定在两块刚性墙体上并加热,金属棒受热膨胀后称为一段圆弧。
现在请你计算圆弧中心点距离原中心点的距离。
【输入数据】
输入数据若干行,每一行,包括三个用空格隔开的非负数字L、n和C。输入数据保证金属棒受热膨胀后的新长度不会超过原长度的1.5倍。
数据结束以 三个-1结束。
【输出数据】
输出数据每行一个数字,表示膨胀后圆弧的中心点离开原中心点的距离,保留三位小数。
Sample Input
1000 100 0.0001
15000 10 0.00006
10 0 0.001
-1 -1 -1
Sample Output
61.329
225.020
0.000
#include
#include
const double esp=1e-5;
int main()
{
double l,n,c,s;
double r;
while(scanf("%lf%lf%lf",&l,&n,&c))
{
if(l<0&&n<0&&c<0)
{
break;
}
double low=0.0;
double high=0.5*l;
double mid;
s=(1+n*c)*l;
while(high-low>esp)
{
mid=(low+high)/2;
r=(4*mid*mid+l*l)/(8*mid);
if( 2*r*asin(l/(2*r)) < s )
low=mid;
else
high=mid;
}
printf("%.3f\n",mid);
}
return 0;
}
例题1: 切割绳子: https://www.luogu.org/problemnew/show/P1577
题目描述:有N条绳子,它们的长度分别为Li。如果从它们中切割出K条长度相同的
绳子,这K条绳子每条最长能有多长?答案保留到小数点后2位。
输入输出格式
输入格式:
第一行两个整数N和K,接下来N行,描述了每条绳子的长度Li。
输出格式:切割后每条绳子的最大长度。
#include
using namespace std;
int n,k;
double a[10005],l,r,mid;
char s[100];
inline bool check(double x)
{
int tot=0;
for(int i=1;i<=n;i++)tot+=floor(a[i]/x);
return tot>=k;
}
int main()
{
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++)scanf("%lf",&a[i]),r+=a[i];
while(r-l>1e-4)
{
mid=(l+r)/2;
if(check(mid))l=mid;
else r=mid;
}
sprintf(s+1,"%.3f",l);
s[strlen(s+1)]='\0';
printf("%s",s+1);
return 0;
}
例题2: 有N本书排成一行,已知第 i 本书的厚度是Ai。把它们分成连续的M组,使T最小化,其中T表示厚度之和最大的一组的厚度。
解析:题目出现了类似“最大值最小”的含义,可以看出答案具有单调性(也就是说这个答案满足在一定单调区间内)。所以可以使用二分搜索,而判定函数如何写呢?假设最大组为size,一共有m组,那么m*size一定小于所有厚度之和;那我们顺序用size减去每本书的厚度,看看能分为几组和小于size且最大,这样一来如果组数小于m,那我们可以通过将一组分割成好几组来凑到m,此时最大厚度不变。而如果组数大于m,我们则可以通过合并来使组数等于m,但这样一来最大厚度就必然大于size。而答案必然存在于1到inf(无穷大),故我们只需找到临界点,即为答案。
bool check(int size){
int cnt = 1;
int tmp = size;
for(int i = 0;i < n;i++){
if(tmp - a[i] >= 0) tmp -= a[i];
else cnt++,tmp = size - a[i];
}
return cnt <= m;
}
int main(){
scanf("%d%d",&n,&m);
for(int i = 0;i < n;i++) scanf("%d",a+i);
int l = 0,r = inf;
while(l < r){
int mid = (r + l )/2;
if(check(mid)) l = mid + 1;
else r = mid;
}
printf("%d\n",l);
return 0;
}
例题3:愤怒的牛 POJ 2456
/*
题意:
有n个牛栏,选m个放进牛,相当于一条线段上有 n 个点,选取 m 个点,
使得相邻点之间的最小距离值最大
思路:贪心+二分
二分枚举相邻两牛的间距,判断大于等于此间距下能否放进所有的牛。
*/
#include
#include
#include
#include
using namespace std;
const int N = 1e6+10;
int a[N],n,m;
bool judge(int k)//枚举间距k,看能否使任意两相邻牛
{
int cnt = a[0], num = 1;//num为1表示已经第一头牛放在a[0]牛栏中
for(int i = 1; i < n; i ++)//枚举剩下的牛栏
{
if(a[i] - cnt >= k)//a[i]这个牛栏和上一个牛栏间距大于等于k,表示可以再放进牛
{
cnt = a[i];
num ++;//又放进了一头牛
}
if(num >= m) return true;//所有牛都放完了
}
return false;
}
void solve()
{
int l = 1, r = a[n-1] - a[0];//最小距离为1,最大距离为牛栏编号最大的减去编号最小的
while(l < r)
{
int mid = (l+r) >> 1;
if(judge(mid)) l = mid + 1;
else r = mid;
}
printf("%d\n",r-1);
}
int main()
{
int i;
while(~scanf("%d%d",&n,&m))
{
for(i = 0; i < n; i ++)
scanf("%d",&a[i]);
sort(a, a+n);//对牛栏排序
solve();
}
return 0;
}