机器学习之模型评估与参数调优
一、流水线工作流
在利用训练数据对模型进行拟合时已经得到一些参数,使用流水线可以避免在将模型用于新数据时重新设置这些参数。利用sklearn中的Pipline类,使得我们可以拟合出包含任意多个处理步骤的模型,并将模型用于新数据的预测。
1. # Title : TODO
2. # Objective : TODO
3. # Created by: Chen Da
4. # Created on: 2018/9/13
5.
6. import pandas as pd
7. import numpy as np
8. import os,time,sys
9.
10. #导入乳腺癌数据集
11. df = pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/wdbc.data",header=None)
12.
13. #构造特征矩阵和类别矩阵
14. from sklearn.preprocessing import LabelEncoder
15. X = df.loc[:, 2:].values
16. y = df.loc[:, 1].values
17. le = LabelEncoder()
18. y = le.fit_transform(y) #对类别进行编码
19.
20. from sklearn.cross_validation import train_test_split
21. X_train, X_test, y_train, y_test = train_test_split(X, y,
22. test_size=0.2, random_state=0)
为了避免对训练集和测试集上的数据分别进行模型拟合、数据转换等操作,这里通过流水线将标准化、PCA和LR回归封装在一起。
1. from sklearn.preprocessing import StandardScaler
2. from sklearn.decomposition import PCA
3. from sklearn.linear_model import LogisticRegression
4. from sklearn.pipeline import Pipeline
5.
6. pip_lr = Pipeline([('std', StandardScaler()),
7. ('PCA', PCA(n_components=2)),
8. ('LR', LogisticRegression(penalty='l1', random_state=0))])
9.
10. pip_lr.fit(X_train, y_train)
11. print("Test score is {}".format(pip_lr.score(X_test, y_test)))
12.
13. Test score is 0.9385964912280702
二、k折交叉检验
通常情况下,我们将k折交叉验证用于模型的调 优,也就是找到使得模型泛化性能 最优的超参值。一旦找到了满意的超参值,我们就可以在全部的训练数据上重新训练模型, 并使用独立的测试数据集对模型性能做出最终评价。分层交叉检验是一种改进的方法,可以得到方差和偏差都较小的结果。
1. from sklearn.cross_validation import StratifiedKFold #分层k折交叉验证
2.
3. kfold = StratifiedKFold(y=y_train,
4. n_folds=10,
5. random_state=0)
6.
7. scores = []
8.
9. for k, (train, test) in enumerate(kfold):
10. # print(k)
11. # print(train,test)
12. pip_lr.fit(X_train[train], y_train[train])
13. score = pip_lr.score(X_train[train], y_train[train])
14. scores.append(score)
15. print("Fold: {}; Class dist: {}; score: {}"
16. .format(k+1, np.bincount(y_train[train]), score))
17.
18. print("CV score is %.3f +/- %.3f" % (np.mean(scores), np.std(scores)))
19.
20.
21. Fold: 1; Class dist: [261 148]; score: 0.960880195599022
22. Fold: 2; Class dist: [261 148]; score: 0.960880195599022
23. Fold: 3; Class dist: [261 148]; score: 0.9633251833740831
24. Fold: 4; Class dist: [261 148]; score: 0.960880195599022
25. Fold: 5; Class dist: [261 148]; score: 0.9755501222493888
26. Fold: 6; Class dist: [261 149]; score: 0.9658536585365853
27. Fold: 7; Class dist: [261 149]; score: 0.9609756097560975
28. Fold: 8; Class dist: [261 149]; score: 0.9658536585365853
29. Fold: 9; Class dist: [261 149]; score: 0.9585365853658536
30. Fold: 10; Class dist: [261 149]; score: 0.9609756097560975
31.
32.
33. CV score is 0.963 +/- 0.005
Sklearn中也封装了k折交叉验证的API:
1. from sklearn.cross_validation import cross_val_score
2.
3. scores = cross_val_score(estimator=pip_lr,
4. X=X_train,
5. y=y_train,
6. n_jobs=-1)
7. print("CV score is %.3f +/- %.3f" % (np.mean(scores), np.std(scores)))
8.
9. CV score is 0.954 +/- 0.014
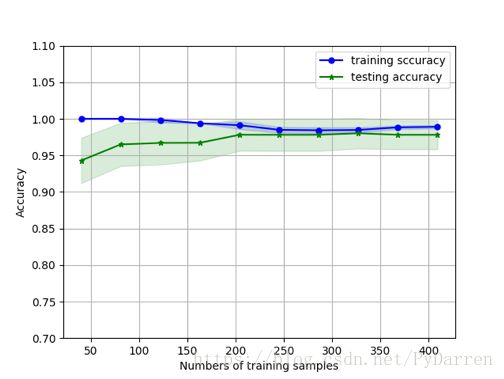
三、利用学习曲线判定方差和偏差
1. import matplotlib.pyplot as plt
2. from sklearn.learning_curve import learning_curve
3.
4. pip_lr = Pipeline([('std', StandardScaler()),
5. ('clf', LogisticRegression(
6. penalty='l2',random_state=1))])
7.
8. train_sizes,train_scores,test_scores = learning_curve(estimator=pip_lr,
9. X=X_train,
10. y=y_train,
11. train_sizes=np.linspace(0.1,1,10),
12. cv=10,
13. n_jobs=-1)
14.
15. # print(train_sizes,train_scores,test_scores)
16.
17. train_mean = np.mean(train_scores,axis=1)
18. train_std = np.std(train_scores,axis=1)
19. test_mean = np.mean(test_scores,axis=1)
20. test_std = np.std(test_scores,axis=1)
21.
22. plt.plot(train_sizes,train_mean,
23. color='blue',marker='o',
24. markersize=5,
25. label='training sccuracy')
26. plt.fill_between(train_sizes,
27. train_mean + train_std,
28. train_mean - train_std,
29. alpha=0.15, color='blue')
30. plt.plot(train_sizes, test_mean,
31. color='green',marker='*',
32. markersize=5,
33. label='testing accuracy')
34. plt.fill_between(train_sizes,
35. test_mean + test_std,
36. test_mean - test_std,
37. color='green',alpha=0.15)
38. plt.grid()
39. plt.xlabel('Numbers of training samples')
40. plt.ylabel('Accuracy')
41. plt.legend(loc='best')
42. plt.ylim([0.7,1.1])
43. plt.savefig('111.png')
44. plt.show()
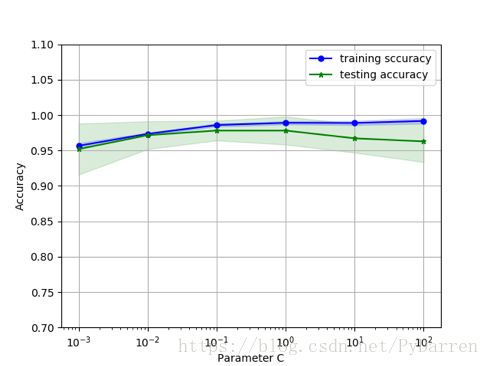
还可以通过验证曲线判定过拟合或者欠拟合来提高模型性能,与学习曲线不同的是,验证曲线绘制的不是样本大小与训练准确率、测试准确率之间的函数关系,而是准确率与模型参数之间的关系。
1. from sklearn.learning_curve import validation_curve
2.
3. param_range = [0.001,0.01,0.1,1,10,100]
4. train_scores, test_scores = validation_curve(estimator=pip_lr,
5. X=X_train,
6. y=y_train,
7. param_name='clf__C',
8. param_range=param_range,
9. cv=10) #这里调整的是LR中的正则系数
10. train_mean = np.mean(train_scores,axis=1)
11. train_std = np.std(train_scores,axis=1)
12. test_mean = np.mean(test_scores,axis=1)
13. test_std = np.std(test_scores,axis=1)
14.
15. plt.plot(param_range,train_mean,
16. color='blue',marker='o',
17. markersize=5,
18. label='training sccuracy')
19. plt.fill_between(param_range,
20. train_mean + train_std,
21. train_mean - train_std,
22. alpha=0.15, color='blue')
23. plt.plot(param_range, test_mean,
24. color='green',marker='*',
25. markersize=5,
26. label='testing accuracy')
27. plt.fill_between(param_range,
28. test_mean + test_std,
29. test_mean - test_std,
30. color='green',alpha=0.15)
31. plt.grid()
32. plt.xscale('log') #x坐标轴刻度按对数取
33. plt.xlabel('Parameter C')
34. plt.ylabel('Accuracy')
35. plt.legend(loc='best')
36. plt.ylim([0.7,1.1])
37. plt.savefig('222.png')
38. plt.show()
关于调优超参的方法常用的还有网格搜索(暴力穷举)、嵌套交叉验证。
四、其他常用的性能评价指标
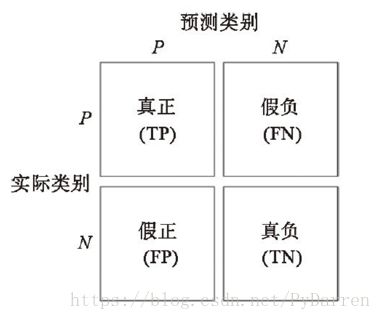
1、混肴矩阵
1. #得到混肴矩阵
2. from sklearn.metrics import confusion_matrix
3. pip_lr.fit(X_train,y_train)
4. y_pred = pip_lr.predict(X_test)
5. confmat = confusion_matrix(y_true=y_test, y_pred=y_pred)
6. print(confmat)
7.
8. [[65 2]
9. [ 2 45]]
10.
11. #得到真正率,召回率,f1分数
12. from sklearn.metrics import precision_score, recall_score, f1_score
13.
14. print("precision score is {}".format(precision_score(y_true=y_test, y_pred=y_pred)))
15. print("recall score is {}".format(recall_score(y_true=y_test, y_pred=y_pred)))
16. print("f1 score is {}".format(f1_score(y_true=y_test, y_pred=y_pred)))
17.
18. precision score is 0.9574468085106383
19. recall score is 0.9574468085106383
20. f1 score is 0.9574468085106385
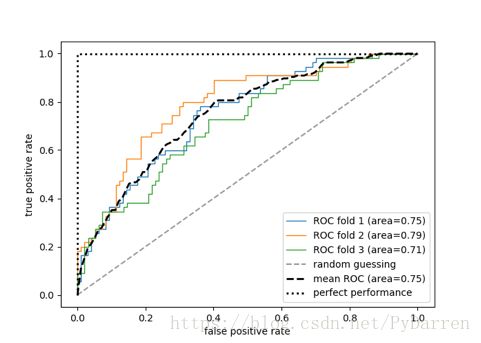
2、ROC曲线
这里给出的是真正率-假正率曲线,也可以绘制真正率-召回率曲线。
1. from sklearn.metrics import roc_curve,auc
2. from scipy import interp
3.
4. X_train2 = X_train[:,[4,14]]
5. cv = StratifiedKFold(y_train,
6. n_folds=3,
7. random_state=0) #分层抽样
8. fig = plt.figure(figsize=(7,5))
9. mean_tpr = 0.0
10. mean_fpr = np.linspace(0,1,100)
11. all_tpr = []
12.
13. for i, (train,test) in enumerate(cv):
14. probas = pip_lr.fit(X_train2[train],
15. y_train[train]).predict_proba(X_train2[test])
16. # print(probas)
17. fpr,tpr,thresholds = roc_curve(y_train[test],
18. probas[:,1],
19. pos_label=1)
20. # print(fpr,tpr,thresholds)
21. mean_tpr += interp(mean_fpr,fpr,tpr) #利用三个块数据对ROC曲线的内插均值进行计算
22. # print(mean_tpr)
23. mean_tpr[0] = 0.0
24. # print(mean_tpr)
25. roc_auc = auc(fpr,tpr)
26. plt.plot(fpr,
27. tpr,
28. lw=1,
29. label='ROC fold %d (area=%0.2f)'
30. % (i+1,roc_auc))
31. plt.plot([0,1],
32. [0,1],
33. linestyle='--',
34. color=(0.6,0.6,0.6),
35. label="random guessing")
36. mean_tpr /= len(cv)
37. mean_tpr[-1] = 1.0
38. mean_auc = auc(mean_fpr,mean_tpr)
39. plt.plot(mean_fpr,
40. mean_tpr,
41. 'k--',
42. label='mean ROC (area=%0.2f)' % mean_auc,
43. lw=2)
44. plt.plot([0,0,1],
45. [0,1,1],
46. lw=2,
47. linestyle=':',
48. color='black',
49. label='perfect performance')
50. plt.xlim([-0.05,1.05])
51. plt.ylim([-0.05,1.05])
52. plt.xlabel('false positive rate')
53. plt.ylabel('true positive rate')
54. plt.legend(loc='best')
55. plt.savefig('333.png')
56. plt.show()