动手学深度学习(tensorflow)---学习笔记整理（三、softmax回归篇）

（有关公式、基本理论等大量内容摘自《动手学深度学习》(TF2.0版)）

什么是softmax回归？

前面学的线性回归最后结果为预测的连续值，而softmax回归更适合预测离散值。这句话可能不太理解。

先说一下softmax的定义：它把一些输入映射为0-1之间的实数，并且归一化保证和为1，因此多分类的概率之和也刚好为1。这些映射的实数的个数是认为设定的。例如我们要识别数字图片，则0-9的概率是我们想要知道的，使用softmax可以预测取0-9的概率，选择0-9之间概率最大的数字作为结果。

加一个官方的样例作一下对比，加深一下了解。

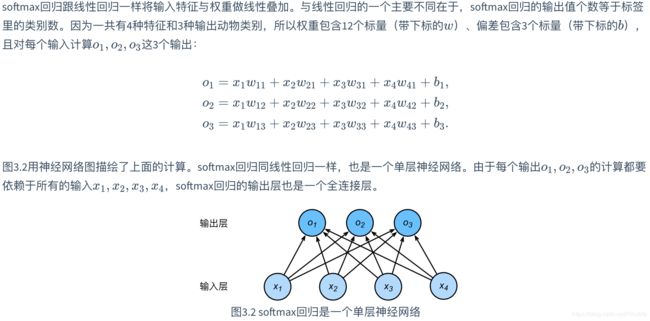
现在看一下比较官方的相关解释：

通过上述公式，可以发现其概率之和为1，其实softmax(o)更类似一个归一化的过程。

单个样本的计算表达式

小批量/多个样本的计算表达式

交叉熵损失函数

这里我将介绍交叉熵损失函数具体如何计算以及为何适合softmax回归分类

假设进行预测“谁偷了我的奶酪”，有两个预测模型其结果如下：

模型1:

实际结果	预测结果	是否正确
0 0 1 （小绿）	0.3 0.3 0.4	正确
0 1 0 （小红）	0.3 0.4 0.3	正确
1 0 0 （小明）	0.1 0.2 0.7	错误

 

模型2:

实际结果	预测结果	是否正确
0 0 1 （小绿）	0.1 0.2 0.7	正确
0 1 0 （小红）	0.1 0.7 0.2	正确
1 0 0 （小明）	0.3 0.4 0.3	错误

通过上述两个模型我们可以发现：模型1对于样本1和样本2以很小的优势判断正确，对于样本3的判断非常错误；模型2对于样本1和样本2判断非常准确，对于样本3判断错误也是微小错误，综上所属模型二明显优于模型一。

下面减少三种评价误差的方法：

     （1）分类错误率/ Classification Error：即错误样本/总样本，上述两个模型 Classification Error均为1/3，无法进行分辨。

     （2）均方误差/Mean Squared Error：内容详见该系列的（二）https://blog.csdn.net/RHJlife/article/details/106344211

模型1:

样例1 loss=(0.3 - 0)^2 + (0.3 - 0)^2 + (0.4 -1 )^2 = 0.54

样例2 loss=(0.3 - 0)^2 + (0.4 - 1)^2 + (0.3 - 0)^2 = 0.54

样例3 loss=(0.1  - 1)^2 + (0.2 - 0)^2 + (0.7 - 0)^2 = 1.32

loss的平均值/MSE=(0.54 + 0.54 + 1.32) / 3 = 0.8

模型2:

样例1 loss=(0.1 - 0)^2 + (0.2 - 0)^2 + (0.7 - 1)^2 = 0.138

样例2 loss=(0.1 - 0)^2 + (0.7 - 1)^2 + (0.2 - 0)^2 = 0.138

样例3 loss=(0.3 - 1)^2 + (0.4 - 0)^2 + (0.3 - 0)^2 = 0.72

loss的平均值/MSE=(0.138 + 0.138 + 0.72) / 3 = 0.332

综上所述，我们能够发现MSE能够判断出来模型2优于模型1。但是为什么不采样这种损失函数呢？

主要原因是逻辑回归配合MSE损失函数时，采用梯度下降法进行学习时，在模型一开始训练时，会出现学习速率非常慢的情况。（内容来自百度，具体我目前也不是很明白～留个坑等评论或者日后更新）

   （3）交叉熵损失函数/Cross Entropy Error Function：公式想见上述，下面展示下如何计算的。

模型1:

样例1 loss=-(0 * log0.3 + 0 * log0.3 + 1 * log0.4) = 0.91

样例2 loss=-(0 * log0.3 + 1 * log0.4 + 0 * log0.3) = 0.91

样例3 loss=-(1  * log0.1 + 0 * log0.2 + 0 * log0.7) = 2.3

loss的平均值/L=(0.91 + 0.91 + 2.3) / 3 = 0.332

模型2:

样例1 loss=-(0 * log0.1 + 0 * log0.2 + 1 * log0.7)  = 0.35

样例2 loss=-(0 * log0.1 + 1 * log0.7 + 0 * log0.2) = 0.35

样例3 loss=-(1 * log0.3 + 0 * log0.4 + 0 * log0.4) = 1.2

loss的平均值/L=(0.35 + 0.35 + 1.2) / 3 = 0.63

综上所述，我们能够发现交叉熵损失函数也能够判断出来模型2优于模型1。

模型的预测

图像分类数据集

MNIST是一个很有名的手写数字识别数据集，也是图像分类数据集中最常用的是手写数字识别数据集, 很多教程都会对它”下手”, 几乎成为一个 “典范”。对于每张图片，存储的方式是一个 28 * 28 的矩阵。文件包括训练集（60000个样本+标签）、测试集（10000个样本+标签）。

可以通过下列命令行直接下载。

from tensorflow.examples.tutorials.mnist import input_data
# location 为保存的文件夹名
mnist = input_data.read_data_sets('location', one_hot=True)

可以输出一些相关信息

from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets('MNIST_data', one_hot=True)

print("type of 'mnist is %s'" % (type(mnist)))
print("number of train data is %d" % mnist.train.num_examples)
print("number of test data is %d" % mnist.test.num_examples)

但因为大部分模型（深度学习+机器学习）在MNIST上的分类精度都很容易超过95%。为了更直观地观察算法之间的差异，我们将使用一个图像内容更加复杂的数据集Fashion-MNIST，日后许多算法也以此为例。

获取数据集

（可能会遇见超时问题：接近方案：过段时间再试试、或者手动下载并加载）

import tensorflow as tf
from tensorflow import keras
import numpy as np
import time
import sys
import matplotlib.pyplot as plt
#下面，我们通过keras的dataset包来下载这个数据集。第一次调用时会自动从网上获取数据。
# 我们通过参数train来指定获取训练数据集或测试数据集（testing data set）。测试数据集只用来评价/检测模型的表现，并不用来训练模型。
from tensorflow.keras.datasets import fashion_mnist
#mnist=input_data.read_data_sets("/Users/ren/anaconda3/envs/tensorflow/lib/python3.6/site-packages/tensorflow_core/python/keras/datasets/fashion-mnist",one_hot=True)
(x_train, y_train), (x_test, y_test) = fashion_mnist.load_data()
#输出长度
print(len(x_train),len(x_test))
#获取第一个样本，可以把0改成任意0-6000之内的数字实现访问任意一个样本
feature,label=x_train[0],y_train[0]
#输出形状和编码
print(feature.shape, feature.dtype)
print(label, type(label), label.dtype)
#Fashion-MNIST中一共包括了10个类别，分别为t-shirt（T恤）、trouser（裤子）、pullover（套衫）、dress（连衣裙）、coat（外套）、sandal（凉鞋）、shirt（衬衫）、sneaker（运动鞋）、bag（包）和ankle boot（短靴）。
# 以下函数可以将数值标签转成相应的文本标签。
def get_fashion_mnist_labels(labels):
    text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat',
                   'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
    return [text_labels[int(i)] for i in labels]
#定义一个可以在一行里画出多张图像和对应标签的函数
def show_fashion_mnist(images, labels):
    _, figs = plt.subplots(1, len(images), figsize=(12, 12))
    for f, img, lbl in zip(figs, images, labels):
        f.imshow(img.reshape((28, 28)))
        f.set_title(lbl)
        f.axes.get_xaxis().set_visible(False)
        f.axes.get_yaxis().set_visible(False)
    plt.show()
X, y = [], []
#输出一下前十个样本看看，训练数据集中前10个样本的图像内容和文本标签
for i in range(10):
    X.append(x_train[i])
    y.append(y_train[i])
show_fashion_mnist(X, get_fashion_mnist_labels(y))
#创建 tf.data.Dataset.from_tensor_slices 实例。
# 该实例每次读取一个样本数为batch_size的小批量数据。这里的批量大小batch_size是一个超参数
batch_size = 256
if sys.platform.startswith('win'):
    num_workers = 0  # 0表示不用额外的进程来加速读取数据
else:
    num_workers = 4
train_iter = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(batch_size)
#查看读取一遍训练数据需要的时间
start = time.time()
for X, y in train_iter:
    continue
print('%.2f sec' % (time.time() - start))

softmax从零实现

import tensorflow as tf
import numpy as np
print(tf.__version__)
from tensorflow.keras.datasets import fashion_mnist
#使用Fashion-MNIST数据集，并设置批量大小为256
batch_size=256
(x_train, y_train), (x_test, y_test) = fashion_mnist.load_data()
#在进行矩阵相乘时需要float型，故强制类型转换为float型
x_train = tf.cast(x_train, tf.float32) / 255
#在进行矩阵相乘时需要float型，故强制类型转换为float型
x_test = tf.cast(x_test,tf.float32) / 255
#创建 tf.data.Dataset.from_tensor_slices 实例，该实例每次读取一个样本数为batch_size的小批量数据
train_iter = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(batch_size)
test_iter = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(batch_size)
#和上述线性回归一样，输入的并非是实际样本，而是向量
#每个样本输入是高和宽均为28像素的图像，所以模型的输入向量的长度是 28×28=784
#该向量的每个元素对应图像中每个像素。由于图像有10个类别，单层神经网络输出层的输出个数为10
#因此softmax回归的权重和偏差参数分别为784×10和1×10的矩阵
num_inputs = 784
num_outputs = 10
W = tf.Variable(tf.random.normal(shape=(num_inputs, num_outputs), mean=0, stddev=0.01, dtype=tf.float32))
b = tf.Variable(tf.zeros(num_outputs, dtype=tf.float32))
#在介绍如何定义 softmax 回归之前，我们先描述一下对如何对多维Tensor按维度操作。
# 在下面的例子中，给定一个Tensor矩阵X。我们可以只对其中同一列（axis=0）或同一行（axis=1）的元素求和，并在结果中保留行和列这两个维度（keepdims=True
X = tf.constant([[1, 2, 3], [4, 5, 6]])
print(tf.reduce_sum(X, axis=0, keepdims=True), tf.reduce_sum(X, axis=1, keepdims=True))
#矩阵logits的行数是样本数，列数是输出个数，完成softmax的计算
def softmax(logits, axis=-1):
    return tf.exp(logits)/tf.reduce_sum(tf.exp(logits), axis, keepdims=True)
#对于任意数进行测试softmax
X = tf.random.normal(shape=(2, 5))
X_prob = softmax(X)
print(X_prob, tf.reduce_sum(X_prob, axis=1))
#定义模型
def net(X):
    #reshpe函数将每张原始图像改成长度为num_inputs的向量
    logits = tf.matmul(tf.reshape(X, shape=(-1, W.shape[0])), W) + b
    return softmax(logits)
#概率和便签进行匹配。
#变量y_hat是2个样本在3个类别的预测概率，变量y是这2个样本的标签类别，boolean_mask讲类别和概率进行连结
y_hat = np.array([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
y = np.array([0, 2], dtype='int32')
#one_hot可以把类别转化为00001这种向量
print(tf.boolean_mask(y_hat, tf.one_hot(y, depth=3)))
#定义损失函数，交叉熵损失函数
def cross_entropy(y_hat, y):
    #cast进行类型转换
    y = tf.cast(tf.reshape(y, shape=[-1, 1]),dtype=tf.int32)
    y = tf.one_hot(y, depth=y_hat.shape[-1])
    y = tf.cast(tf.reshape(y, shape=[-1, y_hat.shape[-1]]),dtype=tf.int32)
    return -tf.math.log(tf.boolean_mask(y_hat, y)+1e-8)
#分类准确率即正确预测数量与总预测数量之比
#tf.argmax(y_hat, axis=1)返回矩阵y_hat每行中最大元素的索引，且返回结果与变量y形状相同。
#相等条件判断式(tf.argmax(y_hat, axis=1) == y)是一个数据类型为bool的Tensor，实际取值为：0（相等为假）或 1（相等为真）。
def accuracy(y_hat, y):
    return np.mean((tf.argmax(y_hat, axis=1) == y))
#进行验证准确率函数
print(accuracy(y_hat, y))
# 描述,对于tensorflow2中，比较的双方必须类型都是int型，所以要将输出和标签都转为int型
#评价模型net在数据集data_iter上的准确率
def evaluate_accuracy(data_iter, net):
    acc_sum, n = 0.0, 0
    for _, (X, y) in enumerate(data_iter):
        y = tf.cast(y,dtype=tf.int64)
        acc_sum += np.sum(tf.cast(tf.argmax(net(X), axis=1), dtype=tf.int64) == y)
        n += y.shape[0]
    return acc_sum / n
print(evaluate_accuracy(test_iter, net))
num_epochs, lr = 5, 0.1
# 本函数已保存在d2lzh包中方便以后使用
def train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, params=None, lr=None, trainer=None):
    for epoch in range(num_epochs):
        train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
        for X, y in train_iter:
            with tf.GradientTape() as tape:
                y_hat = net(X)
                l = tf.reduce_sum(loss(y_hat, y))
            grads = tape.gradient(l, params)
            if trainer is None:
                # 如果没有传入优化器，则使用原先编写的小批量随机梯度下降
                for i, param in enumerate(params):
                    param.assign_sub(lr * grads[i] / batch_size)
            else:
                # tf.keras.optimizers.SGD 直接使用是随机梯度下降 theta(t+1) = theta(t) - learning_rate * gradient
                # 这里使用批量梯度下降，需要对梯度除以 batch_size, 对应原书代码的 trainer.step(batch_size)
                trainer.apply_gradients(zip([grad / batch_size for grad in grads], params))

            y = tf.cast(y, dtype=tf.float32)
            train_l_sum += l.numpy()
            train_acc_sum += tf.reduce_sum(tf.cast(tf.argmax(y_hat, axis=1) == tf.cast(y, dtype=tf.int64), dtype=tf.int64)).numpy()
            n += y.shape[0]
        test_acc = evaluate_accuracy(test_iter, net)
        print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'% (epoch + 1, train_l_sum / n, train_acc_sum / n, test_acc))
#进行训练
trainer = tf.keras.optimizers.SGD(lr)
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, batch_size, [W, b], lr)
#预测结果
import matplotlib.pyplot as plt
X, y = iter(test_iter).next()
print(X,y)
#根据0-9的数字转化为具体标签
def get_fashion_mnist_labels(labels):
    text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat', 'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
    return [text_labels[int(i)] for i in labels]
#现实图片+预测标签+实际标签
def show_fashion_mnist(images, labels):
    # 这⾥的_表示我们忽略（不使⽤）的变量
    _, figs = plt.subplots(1, len(images), figsize=(12, 12)) # 这里注意subplot 和subplots 的区别
    for f, img, lbl in zip(figs, images, labels):
        f.imshow(tf.reshape(img, shape=(28, 28)).numpy())
        f.set_title(lbl)
        f.axes.get_xaxis().set_visible(False)
        f.axes.get_yaxis().set_visible(False)
    plt.show()

true_labels = get_fashion_mnist_labels(y.numpy())
pred_labels = get_fashion_mnist_labels(tf.argmax(net(X), axis=1).numpy())
titles = [true + '\n' + pred for true, pred in zip(true_labels, pred_labels)]

show_fashion_mnist(X[0:9], titles[0:9])

softmax的简洁实现

import tensorflow as tf
from tensorflow import keras
#读取数据集
fashion_mnist = keras.datasets.fashion_mnist
(x_train, y_train), (x_test, y_test) = fashion_mnist.load_data()
#归一化
x_train = x_train / 255.0
x_test = x_test / 255.0
#定义模型
model = keras.Sequential([
    keras.layers.Flatten(input_shape=(28, 28)),
    keras.layers.Dense(10, activation=tf.nn.softmax)
])
#设置损失函数
loss = 'sparse_categorical_crossentropy'
#定义优化函数
optimizer = tf.keras.optimizers.SGD(0.1)
#训练模型
model.compile(optimizer=tf.keras.optimizers.SGD(0.1),
              loss = 'sparse_categorical_crossentropy',
              metrics=['accuracy'])

model.fit(x_train,y_train,epochs=5,batch_size=256)