常用统计学回归模型应用场景与python实现方法

常用统计学回归模型应用场景与python实现方法

在信息管理、数据科学或fintech等研究中，有时会遇到统计学回归模型，那么这些基本统计回归模型的使用场景是什么？该如何用python快捷的实现统计回归呢？本文从数据类型出发对统计回归模型进行了分类整理，并基于python的statsmodel库（类R语言），给出了这些模型的一种实现方案。

一、理清数据类型：横截面数据、时间序列数据、分层数据or面板数据

为了下文表达清晰，构造一张经典表如下：

Table 1	2000	2001	2002	2000	2001	2002	2000	2001	2002
北京	9	10	11	12	13	14	15	16	17
上海	8	9	10	11	12	13	14	15	16
天津	5	6	7	8	9	10	11	12	13

• 横截面数据：同一时间，不同统计单位相同统计指标组成的数据列，按照统计单位排列。如：

Table 2	2000
北京	9
上海	8
天津	5

• 时间序列数据：某事物、现象随时间的变化状态，即它在不同时间点的数据。如：

Table 3	2000	2001	2002	2000	2001
北京	9	10	11	12	13

• 分层数据： 不仅有描述个体的变量，而且有个人组成的更高一层的变量(可以包括若干层具有层次结构的变量)。如Table 4：

省	区	2000	2001	2002	2000
北京	海淀	2	3	4	5
北京	朝阳	1	2	3	4

• 面板数据： 由截面数据和时间序列数据综合而来的数据类型。如Table 1所示。

二、明确因变量类型：连续变量、计数变量、分类变量

• 连续变量：数值是连续不断的
• 计数变量：变量值只能取非负整数{0,1,2,3,...}。这个变量来自计数（count）而非排名。
• 分类变量：变量值是定性的，表现为互不相容的类别或属性。如类别1、属性2。分为无需变量和有序变量两类。

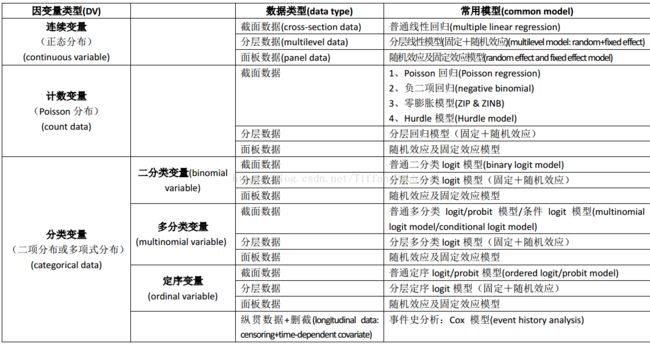
三、选择统计回归模型：

四、常用回归模型的python实现：

• 使用http://www.scipy-lectures.org/_downloads/brain_size.csv脑容量数据举例，样例如下：
• 1、利用pandas读取数据并保存成dataframe：

import pandas

data = pandas.read_csv('brain_size.csv', sep=';', na_values=".")

• 2、利用线性模型比较男女IQ值（其中类别"Gender"被自动识别为分类变量）

model = ols("VIQ ~ Gender + 1", data).fit()
print(model.summary())

 OLS Regression Results                           

==============================================================================

Dep. Variable:                    VIQ   R-squared:                       0.015

Model:                            OLS   Adj. R-squared:                 -0.010

Method:                 Least Squares   F-statistic:                    0.5969

Date:                Tue, 09 May 2017   Prob (F-statistic):              0.445

Time:                        17:45:59   Log-Likelihood:                -182.42

No. Observations:                  40   AIC:                             368.8

Df Residuals:                      38   BIC:                             372.2

Df Model:                           1                                         

Covariance Type:            nonrobust                                         

==================================================================================

                     coef    std err          t      P>|t|      [0.025      0.975]

----------------------------------------------------------------------------------

Intercept        109.4500      5.308     20.619      0.000      98.704     120.196

Gender[T.Male]     5.8000      7.507      0.773      0.445      -9.397      20.997

==============================================================================

Omnibus:                       26.188   Durbin-Watson:                   1.709

Prob(Omnibus):                  0.000   Jarque-Bera (JB):                3.703

Skew:                           0.010   Prob(JB):                        0.157

Kurtosis:                       1.510   Cond. No.                         2.62

==============================================================================

• 3、线性多元回归模型探究体重、身高、性别对IQ值（连续值）的影响

model = ols('VIQ ~ Gender + Weight + Height', data).fit()

print(model.summary())

 OLS Regression Results                           

==============================================================================

Dep. Variable:                    VIQ   R-squared:                       0.108

Model:                            OLS   Adj. R-squared:                  0.029

Method:                 Least Squares   F-statistic:                     1.369

Date:                Tue, 09 May 2017   Prob (F-statistic):              0.269

Time:                        17:52:24   Log-Likelihood:                -170.29

No. Observations:                  38   AIC:                             348.6

Df Residuals:                      34   BIC:                             355.1

Df Model:                           3                                         

Covariance Type:            nonrobust                                         

==================================================================================

                     coef    std err          t      P>|t|      [0.025      0.975]

----------------------------------------------------------------------------------

Intercept        261.8374     88.157      2.970      0.005      82.680     440.995

Gender[T.Male]    20.4303     10.822      1.888      0.068      -1.562      42.423

Weight            -0.1012      0.230     -0.441      0.662      -0.568       0.366

Height            -2.1059      1.490     -1.414      0.167      -5.134       0.922

==============================================================================

Omnibus:                        7.582   Durbin-Watson:                   2.159

Prob(Omnibus):                  0.023   Jarque-Bera (JB):                2.540

Skew:                          -0.231   Prob(JB):                        0.281

Kurtosis:                       1.820   Cond. No.                     4.03e+03

==============================================================================

• 4、利用medpar数据集进行负二项式回归例子（因变量为计数变量）

数据样例：

los  hmo  white  died  age80  type  type1  type2  type3  provnum

0    4    0      1     0      0     1      1      0      0    30001

1    9    1      1     0      0     1      1      0      0    30001

2    3    1      1     1      1     1      1      0      0    30001

3    9    0      1     0      0     1      1      0      0    30001

4    1    0      1     1      1     1      1      0      0    30001

#example for Negative Binomial Regression for Count Data

medpar = sm.datasets.get_rdataset("medpar", "COUNT", cache=True).data

y = medpar.los

X = medpar[["type2", "type3", "hmo", "white"]].copy()

X["constant"] = 1

res_nbin = NegativeBinomial(y, X).fit(disp=0)

print(res_nbin.summary())

 NegativeBinomial Regression Results                     

==============================================================================

Dep. Variable:                    los   No. Observations:                 1495

Model:               NegativeBinomial   Df Residuals:                     1490

Method:                           MLE   Df Model:                            4

Date:                Tue, 09 May 2017   Pseudo R-squ.:                 0.01215

Time:                        18:13:53   Log-Likelihood:                -4797.5

converged:                       True   LL-Null:                       -4856.5

                                        LLR p-value:                 1.404e-24

==============================================================================

                 coef    std err          z      P>|z|      [0.025      0.975]

------------------------------------------------------------------------------

type2          0.2212      0.051      4.373      0.000       0.122       0.320

type3          0.7062      0.076      9.276      0.000       0.557       0.855

hmo           -0.0680      0.053     -1.277      0.202      -0.172       0.036

white         -0.1291      0.069     -1.883      0.060      -0.263       0.005

constant       2.3103      0.068     34.001      0.000       2.177       2.443

alpha          0.4458      0.020     22.495      0.000       0.407       0.485

==============================================================================

• 5、利用medpar数据集进行Poisson回归例子

#poisson regression model

poisson = Poisson(y, X).fit()

print(poisson.summary())

Optimization terminated successfully.

         Current function value: 4.634721

         Iterations 21

                          Poisson Regression Results                         

==============================================================================

Dep. Variable:                    los   No. Observations:                 1495

Model:                        Poisson   Df Residuals:                     1490

Method:                           MLE   Df Model:                            4

Date:                Tue, 09 May 2017   Pseudo R-squ.:                 0.05189

Time:                        18:21:46   Log-Likelihood:                -6928.9

converged:                       True   LL-Null:                       -7308.1

                                        LLR p-value:                7.600e-163

==============================================================================

                 coef    std err          z      P>|z|      [0.025      0.975]

------------------------------------------------------------------------------

type2          0.2217      0.021     10.529      0.000       0.180       0.263

type3          0.7095      0.026     27.146      0.000       0.658       0.761

hmo           -0.0715      0.024     -2.988      0.003      -0.118      -0.025

white         -0.1539      0.027     -5.613      0.000      -0.208      -0.100

constant       2.3329      0.027     85.744      0.000       2.280       2.386

==============================================================================

、

更多模型，可自行参考python statsmodels doc: http://www.statsmodels.org/stable/。

参考：

1. 常用回归模型：https://wenku.baidu.com/view/1b124799daef5ef7ba0d3cee.html
2. http://www.scipy-lectures.org/packages/statistics/index.html
3. http://www.statsmodels.org/stable/
4. python中的统计学：https://wizardforcel.gitbooks.io/scipy-lecture-notes/content/14.html