IPVS和Nginx两种WRR负载均衡算法详解

动机

五一临近，四月也接近尾声，五一节乃小长假的最后一天。今天是最后一天工作日，竟然感冒了，半夜里翻来覆去无法安睡，加上窗外大飞机屋里小飞机(也就是蚊子)的骚扰，实在是必须起来做点有意义的事了！

  忆起与人交流一个负载均衡问题时，偶然聊到了WRR算法，就必然要记下些什么，以表示曾经聊过这个话题，作此文以记之！

简介

在负载均衡场景中，我们经常需要对一组服务器做加权轮询均衡调用，即适配一个叫做WRR(Weighted Round-Robin Scheduling)的算法。本文的主要内容就是分析常见的两种WRR算法，即Linux IPVS的WRR算法和Nginx的WRR算法，并试图做出二者的比较。

  当然了，负载均衡的算法非常多，但很难在一篇技术随笔中盖以全貌，与其说不透，不如干脆不说，因此本文的内容仅仅包含两种常见的WRR算法。

Linux内核IPVS使用的WRR算法

这里接不介绍IPVS了，直接切入算法本身，详见net/netfilter/ipvs/ip_vs_wrr.c中的结构体：

static struct ip_vs_scheduler ip_vs_wrr_scheduler = {
    .name =         "wrr",
    .refcnt =       ATOMIC_INIT(0),
    .module =       THIS_MODULE,
    .n_list =       LIST_HEAD_INIT(ip_vs_wrr_scheduler.n_list),
    .init_service =     ip_vs_wrr_init_svc,
    .done_service =     ip_vs_wrr_done_svc,
    .add_dest =     ip_vs_wrr_dest_changed,
    .del_dest =     ip_vs_wrr_dest_changed,
    .upd_dest =     ip_vs_wrr_dest_changed,
    .schedule =     ip_vs_wrr_schedule,
};

这里重点关注schedule 回调函数ip_vs_wrr_schedule。

  为了让事情更加直观，不至于陷入到Linux内核源码IPVS复杂业务逻辑的深渊，这里给出其Wiki上上的写法，摘自：http://kb.linuxvirtualserver.org/wiki/Weighted_Round-Robin_Scheduling：

Supposing that there is a server set S = {S0, S1, …, Sn-1};
W(Si) indicates the weight of Si;
i indicates the server selected last time, and i is initialized with -1;
cw is the current weight in scheduling, and cw is initialized with zero; 
max(S) is the maximum weight of all the servers in S;
gcd(S) is the greatest common divisor of all server weights in S;

while (true) {
    i = (i + 1) mod n;
    if (i == 0) {
        cw = cw - gcd(S); 
        if (cw <= 0) {
            cw = max(S);
            if (cw == 0)
            return NULL;
        }
    } 
    if (W(Si) >= cw) 
        return Si;
}

如果你还是没有一个直观上的感受，下面是我写的一个简单的能run的程序，直接编译运行即可：

#include 
#include 

struct entry {
        int weight;
};

struct entry *g_entry = NULL;
int max_weight = 0;
int curr_weight = 0;
int divisor = 0;
int iter = -1;


int gcd(int a, int b)  
{  
        if (a == 0) {
                return b;
        }
        return gcd(b%a, a);  
} 

struct entry *next(int size) 
{

        struct entry *ent;
        while (1) {
                iter = (iter + 1) % size;
                if (iter == 0) {
                        curr_weight = curr_weight - divisor; 
                        if (curr_weight <= 0) {
                                curr_weight = max_weight;
                        }
                } 
                ent = &g_entry[iter];
                if (ent->weight >= curr_weight) {
                        return ent;
                }
        }
}

int main(int argc, char **argv)
{
        int size = atoi(argv[1]);
        int i = 0;
        int total = 0;

        g_entry = (struct entry *)calloc(size, sizeof(struct entry));
        for (i = 0; i < size; i++) {
                struct entry *ent = &g_entry[i];
                ent->weight = atoi(argv[i+2]);
                total += ent->weight;
                if (ent->weight > max_weight) {
                        max_weight = ent->weight;
                }
                divisor = gcd(divisor, ent->weight);
        }

        for (i = 0; i < total; i++) {
                struct entry *ent = next(size);
                printf("[LAST]: %d\n", ent->weight);
        }

}

你可以这样使用这个程序：

# 这里生成一个3(第一个参数)个元素的集合，其权值分别为5,1,1(后面的参数)
./a.out 3 5 1 1

简单的证明和分析

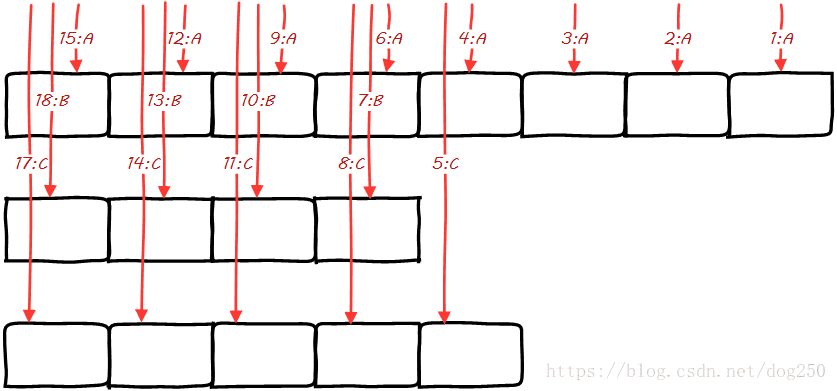
这个算法给出的结果总是正确的吗？回答这个问题我觉得非常简单直观，请看下图：

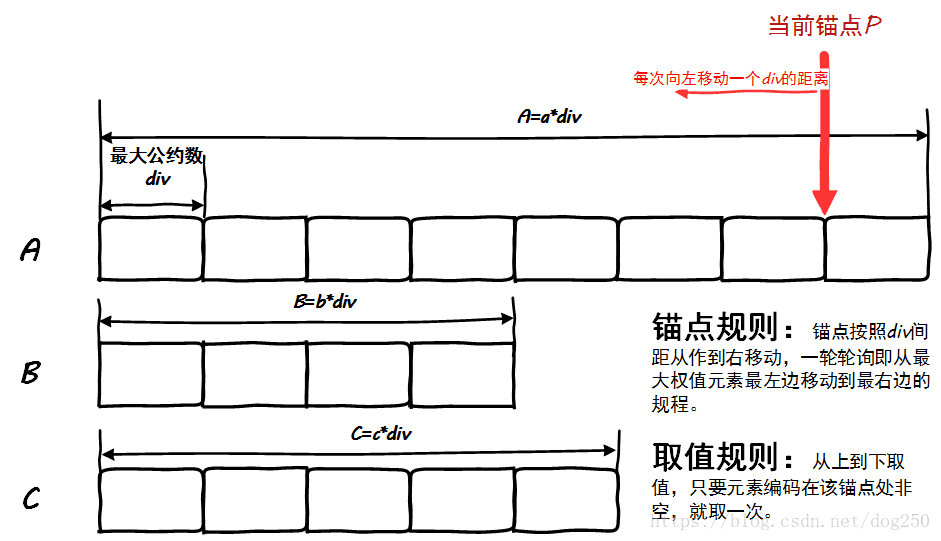
按照上图中的规则，取元素的顺序则是：

---

在数学上证明算法的正确性似乎也不难，设一个元素的权值为 Wi W i ，那么它在锚点一轮轮询中被选中的次数就是 Widiv W i d i v ，可见，对于一个固定的序列，其 div d i v 一定，一个元素被选中的次数与其权值成正比，这便符合了算法的要求。

问题

观察上面的图，如果一个集合中最大权值的元素和次大权值的元素相隔太远，那么这个算法在选元素的时候是不会把权值大的元素打散的，比如：

root@debian:/home/zhaoya# ./a.out 2 5 1
[LAST]: 5
[LAST]: 5
[LAST]: 5
[LAST]: 5
[LAST]: 5
[LAST]: 1

映射回负载均衡的真实场景，这显然会对某些大权值的服务器造成很大的压力，因此对这个算法的改进或者说换另外一个算法是一件必须要做的事。接下来我们就开始分析一个结果序列更加平均的WRR算法，即Nginx服务器中使用的WRR算法。

---

Nginx使用的WRR算法

关于这个算法，具体的描述详见：
https://github.com/phusion/nginx/commit/27e94984486058d73157038f7950a0a36ecc6e35

和分析IPVS之WRR算法的做法一样，我依然给出一个能run的代码，其运行方法与上述IPVS的算法完全一致：

#include 
#include 

struct entry {
        int weight;
        int curr_weight;
};

struct entry *curr_entry = NULL;
struct entry *g_entry = NULL;

struct entry *next(struct entry *entrys, int size) 
{

        struct entry *ent;
        int i = 0, total = 0;
        for (i = 0; i < size; i++) {
                ent = &entrys[i];
                ent->curr_weight += ent->weight;
                total += ent->weight;
                if (curr_entry == NULL || ent->curr_weight > curr_entry->curr_weight) {
                        curr_entry = ent;
                }
        }
        curr_entry->curr_weight -= total;
        for (i = 0; i < size; i++) {
                ent = &entrys[i];
        }
        return curr_entry;
}

int main(int argc, char **argv)
{
        int size = atoi(argv[1]);
        int i = 0;
        int total = 0;

        g_entry = (struct entry *)calloc(size, sizeof(struct entry));
        for (i = 0; i < size; i++) {
                struct entry *ent = &g_entry[i];
                ent->weight = atoi(argv[i+2]);
                total += ent->weight;
        }


        for (i = 0; i < total; i++) {
                struct entry *ent = next(g_entry, size);
                printf("[LAST]: %d\n", ent->weight);
        }

}

以上就是Nginx所采用的WRR算法的代码描述，在大多数情况下，采用这种算法是一个不错的选择。即满足了固定的加权平均，又使得元素的选择尽可能地分散开来，非常精妙！

  该算法与IPVS的WRR按照某种规则和组织静态遍历完全不同，它完全是一个动态的过程，因此除非用动画，否则一张图无法展示全貌。我用简单的3个元素加权来描述一下这个算法。假设有3个具有不同权值的 {A:a,B:b,C:c} { A : a , B : b , C : c } 元素供选择，在一轮轮询中，3个元素分别被递加其权值的递增量为：

元素 A A 递增 a a 的量： a×(a+b+c) a × ( a + b + c )
元素 B B 递增 b b 选中的量： b×(a+b+c) b × ( a + b + c )
元素 C C 递增 c c 选中的量： c×(a+b+c) c × ( a + b + c )

每选中一个元素，将会从其递增量中减去 (a+b+c) ( a + b + c ) ，那么很显然，问题部分地被转化为求出每个元素递增量中包含多少个递减量便是该元素会被选中的次数。最终，我们承认下面的解是一个正确的解：

元素 A A 被选中的次数： a×(a+b+c)a+b+c a × ( a + b + c ) a + b + c 次
元素 B B 被选中的次数： b×(a+b+c)a+b+c b × ( a + b + c ) a + b + c 次
元素 C C 被选中的次数： c×(a+b+c)a+b+c c × ( a + b + c ) a + b + c 次

  然而，这个解是唯一的解吗？如何证明这是唯一解？这便是一个数学问题。理解并使用该算法是完全没有问题的，coders深谙此道，然而想要彻底理解它，则必须要证明在算法的操作下，最终得到的解是唯一解，接下来我就简单用反证法来证明一下。

算法的描述

这个算法很有意思，所有集合一开始各就各位初始化自己的 Wcurri W c u r r i 为自己的权值，然后谁获胜(即其 Wcurri W c u r r i 最大)，谁就要减掉所有元素的权值之和 (a+b+c) ( a + b + c ) ，接下来继续推进一步，每一个元素再加上自己的权值…最终我们发现，每一步推进过程，每一个元素各自增加自身的权值，然后获胜者把所有元素增加的权值一次性做减法，这意味着，任何时候，在选择元素前：

ΣWcurri=a+b+c Σ W c u r r i = a + b + c

而选择了 Wcurri W c u r r i 最大的元素后：

ΣWcurri=0 Σ W c u r r i = 0

这像不像古代军队弓箭手放乱箭的过程，简直太像了！同时，这是一种非积累即时消费的模型，即获胜者一次性消费掉其它选手在本轮中获取的配额。这种非积累特性抹掉了很多潜在的记忆阻止了幂律产生作用，让结果散列地更均匀。

---

算法正确性证明

假设在集合 {A:a,B:b,C:c} { A : a , B : b , C : c } 尚未取够 (a+b+c) ( a + b + c ) 个元素的时候，权重为 a a 的元素 A A 已经取满了 a a 个，此时：

Wcurra=N×a−(a−1)(a+b+c) W c u r r a = N × a − ( a − 1 ) ( a + b + c )
Wcurrb=N×b−mb1(a+b+c) W c u r r b = N × b − m b 1 ( a + b + c )
Wcurrc=N×c−mc1(a+b+c) W c u r r c = N × c − m c 1 ( a + b + c )

由算法基本逻辑，我们知道上面 3 3 式子相加等于 (a+b+c) ( a + b + c ) ：

ΣWcurri=N×(a+b+c)−(a−1+mb1+mc1)(a+b+c)=(a+b+c) Σ W c u r r i = N × ( a + b + c ) − ( a − 1 + m b 1 + m c 1 ) ( a + b + c ) = ( a + b + c )

化简得到：

N=a+mb1+mc1 N = a + m b 1 + m c 1    (1) ( 1 )

现在假设，在取到第 T T (N<T<a+b+c) ( N < T < a + b + c ) 个的时候，又取了一个权重为 a a 的元素 A A ，则此时根据算法逻辑计算 Wcurri W c u r r i ：

Wcurra=T×a−(a+mT−1)(a+b+c) W c u r r a = T × a − ( a + m T − 1 ) ( a + b + c )    mT m T 为此间取到 A A 的次数
Wcurrb=T×b−mb2(a+b+c) W c u r r b = T × b − m b 2 ( a + b + c )
Wcurrc=T×c−mc2(a+b+c) W c u r r c = T × c − m c 2 ( a + b + c )

又因为取到权值为 a a 的元素 A A 的条件是此时其 Wcurr W c u r r 最大，则有：

T×a−(a+mT−1)(a+b+c)>T×b−mb2(a+b+c) T × a − ( a + m T − 1 ) ( a + b + c ) > T × b − m b 2 ( a + b + c )
T×a−(a+mT−1)(a+b+c)>T×c−mc2(a+b+c) T × a − ( a + m T − 1 ) ( a + b + c ) > T × c − m c 2 ( a + b + c )

化简上面式子：

T×(a−b)>(a+mT−1−mb2)(a+b+c) T × ( a − b ) > ( a + m T − 1 − m b 2 ) ( a + b + c )
T×(a−c)>(a+mT−1−mc2)(a+b+c) T × ( a − c ) > ( a + m T − 1 − m c 2 ) ( a + b + c )

根据条件 N<T<a+b+c N < T < a + b + c 代入，则有：

T×(a−b)>(a+mT−1−mb2)×T T × ( a − b ) > ( a + m T − 1 − m b 2 ) × T
T×(a−c)>(a+mT−1−mc2)×T T × ( a − c ) > ( a + m T − 1 − m c 2 ) × T

最终，我们得到两个不等式：

mb2−b>mT−1 m b 2 − b > m T − 1
mc2−c>mT−1 m c 2 − c > m T − 1

由于我们是在第 T T 次取的第 a+1 a + 1 个权值为 a a 的元素 A A ，所以这里的 m m 等于 1 1 ，则有：

mb2−b>0 m b 2 − b > 0
mc2−c>0 m c 2 − c > 0

现在谜底要揭开了！由于我们假设在集合 {A:a,B:b,C:c} { A : a , B : b , C : c } 取完 a+b+c a + b + c 个元素之后，权值为 a a 的元素 A A 的取量多于 a a 个，那么权值为 b b 和 c c 的元素 B B 和 C C 取量必然至少有一个要少于自己权重数值，而上面的不等式表明，若需要满足权值为 a a 的元素 A A 的取量多于 a a 个，权值为 b b 和 c c 的元素 B B 和 C C 取量也必须同时多于它们的权值！这显然最终会造成一个矛盾：

ma+mb+mc>a+b+c m a + m b + m c > a + b + c

因此，假设是错误的！即：

权值为 a a 的元素 A A 在一轮轮询之后的取量不可能多于 a a 个

那么，能不能少于 a a 个呢？这个问题很简单！既然 A A 元素少于 a a 个，那么在总量 a+b+c a + b + c 一定的情况下，一定有别的元素的取量多于自己的权值，因此问题还是会转化为上面我们反证的问题，这实际上是同一个问题！

---

好了，本节我们证明了Nginx里面的这个WRR算法是正确的，即通过算法指示的操作，算法轮询结束后，会严格按照元素的权值比例分配被轮询的次数。

为什么比IPVS的WRR要好？

这个问题其实很难回答，因为很难有一个确定的标准。我咨询过很多大师大神，得到的答案几乎都是从概率，global state的变更频率以及最大熵的角度来分析，然而这些对于回到这个问题有点复杂了。因为我知道Nginx的WRR算法也远不是最好的，其序列分布也不满足最大熵…

  所以，我把问题化简，我只要能求出一个权值最大的元素在序列一开始时连续分布的最大上界就基本OK了，如果我求出的这个上界小于其权值 Wi W i ，那就可以说明不可能所有的最大权值的元素完全连续分布，但确实要连续分布一点点，这便打散了整个分布，这已经比IPVS的WRR算法最终的序列分布要好了。

  现在让我们开始。

---

假设元素 A A 的权值最大，为 a a ，设其连续分布 x x 次，则有：

x×a−(x−1)(a+b+c)>0 x × a − ( x − 1 ) ( a + b + c ) > 0

上面式子的含义是，选最后一次 A A 的时候，其配额依然是正的。现在化简：

x<a+b+cb+c x < a + b + c b + c

这就是上界！

  好吧，我现在用一个更加极端的例子来展示一下：

root@debian:/home/zhaoya# ./a.out 2 18 1
[LAST]: 18
[LAST]: 18
[LAST]: 18
[LAST]: 18
[LAST]: 18
[LAST]: 18
[LAST]: 18
[LAST]: 18
[LAST]: 18
[LAST]: 1
[LAST]: 18
[LAST]: 18
[LAST]: 18
[LAST]: 18
[LAST]: 18
[LAST]: 18
[LAST]: 18
[LAST]: 18
[LAST]: 18

很显然， 18 18 连续了 9 9 次，按照上界公式算出来18连续分布应该不超过19次，显然9没有超过19，这是正确的。那么如何解释中间插入的那个1呢？显然，这就是算法的精妙之所在。

  按照算法描述，每选中一个最大值 Wcurri W c u r r i 元素，其 Wcurri W c u r r i 便需要减去配额 (a+b+c) ( a + b + c ) ，与此同时，其它落选的元素其 Wcurri W c u r r i 是单调递增的，这是一个小学四年级就学过的相遇问题，这从根本上阻止了任意元素的连续分布！

  依然以3个元素的集合为例，假设元素 A A 的权值最大，为 a a ，元素 B B 的权值次大(我们需要次大的元素与最大的元素的 Wcurri W c u r r i 相遇)，为 b b ，按照相遇问题的解法，我们有：

a−x×(b+c)=x×b a − x × ( b + c ) = x × b

化简为：

x=a2b+c x = a 2 b + c

在下面的例子中代入上式：

root@debian:/home/zhaoya# ./a.out 2 18 1

我们得到 x=9 x = 9 。

  当然，在这里我有意把问题简化了，因此这不是一个普通的相遇问题，因此上面式子中的等号 = = 是不恰当的，但无论如何，我展示了一个极端情况下Nginx WRR算法的表现。

算法的O(n)问题

很多人对本文中所描述的两种WRR算法并不是很满意，因为在寻找next元素的时候，其时间复杂度是 O(n) O ( n ) 的，人们一般很讨厌看到这个 O(n) O ( n ) ！

  但是实际上，这并无所谓，虽然是 O(n) O ( n ) ，但是还有一件利器，即cache的思路，或者说网络上转控分离思路来解决这个 O(n) O ( n ) 的问题。

  在不考虑权值动态更新的前提下，事实上，给定一个集合，按照权值的WRR分布是一个固定的序列，我们不妨在第一次获取到这个序列的时候就将其保存起来，随便用什么基于定位而非查找的数据结构都可以，比如数组，bitmap这种，总之就是在后续的操作中，用 O(1) O ( 1 ) 的时间复杂度来定位集合中的next元素！

  这类似将WRR做了一个预处理，事先生成了序列。

CFS/FQ/PQ调度与WRR负载均衡

最后来比较一下WRR和FQ队列。

  FQ队列以及PQ队列以及队列领域的WRR算法注重于在时间上调度上的公平性，即完全按照其优先级权值来进行调度，谁的权值大，谁优先。

  而负载均衡中的WRR更多的是在空间上考虑公平性，在空间维度，打散结果是最好的方案。

  其实，我们也可以按照队列调度的思想来重新实现负载均衡的WRR算法，以下是一个简单的代码，参照Linux CFS调度器的原理：

#include 
#include 

struct entry {
        int weight;
        int curr_cfs;
};

struct entry *curr_entry = NULL;
struct entry *g_entry = NULL;


struct entry *next_cfs(struct entry *entrys, int size)
{
        struct entry *ent;
        int i = 0, total = 0;
        for (i = 0; i < size; i++) {
                ent = &entrys[i];
                // 选择最小的curr_cfs
                if (curr_entry == NULL || ent->curr_cfs < curr_entry->curr_cfs) {
                        curr_entry = ent;
                }
        }
    // 满足“单位1”中有weight个元素，算法的结果才是正确的
        curr_entry->curr_cfs += 100000000/(curr_entry->weight);
        return curr_entry;
}


int main(int argc, char **argv)
{
        int size = atoi(argv[1]);
        int i = 0;
        int total = 0;

        g_entry = (struct entry *)calloc(size, sizeof(struct entry));
        for (i = 0; i < size; i++) {
                struct entry *ent = &g_entry[i];
                ent->weight = atoi(argv[i+2]);
                ent->curr_cfs = 100000000/ent->weight;
                total += ent->weight;
        }


        for (i = 0; i < total; i++) {
                struct entry *ent = next_cfs(g_entry, size);
                printf("[LAST_CFS]: %d\n", ent->weight);
        }

}

你可以试一下结果。你会发现，所有权值一样的元素完全挤在一起了，这非常符合在时间序列上的公平性表现(大体上，进程调度和数据包调度都是如此表现)，但是在空间维度上却非常差劲。

后记

生日过后，待续！